使用Gaussian做鑭系金屬配合物的量子化學計算

使用Gaussian做鑭系金屬配合物的量子化學計算

文/Sobereva@北京科音 2021-Jan-13

0 前言

過渡金屬配合物體系的量子化學計算比主族體系的計算通常更復雜，因為在判斷自旋多重度方面需要更多考慮，SCF收斂整體更難（d軌道近簡并所致），而且還有更高幾率收斂到不穩定波函數。而鑭系錒系配合物的計算甚至更困難，由于f軌道近簡并導致SCF比過渡金屬配合物還更難收斂（除非鑭系錒系原子用大核贗勢，此時不需要描述f電子），檢測波函數穩定性的必要性更高，而且中心金屬配位數也往往更高、考慮更復雜。本文給大家一個用Gaussian做DFT計算鑭系金屬配合物12-冠-4-五水合鈥(III)陽離子的例子，希望通過此例令讀者了解到鑭系錒系金屬配合物計算的相關知識和需要注意的相關問題，從而能舉一反三地研究其它此類體系。

注：如果你的量子化學研究經驗有限，本文提到的所有博文都要讀，否則本文里一些說明難以充分、正確理解。如果你連用Gaussian算有機類體系都還不能熟練地計算，不建議現階段看此文然后就開始一通折騰鑭系錒系計算，應當看的是《談談學量子化學如何正確地入門》（http://www.shanxitv.org/355）。

本文用到的計算程序是Gaussian 16 A.03，本文所談的與Gaussian有關的情況對于這個版本都是適用的。相關分析用的是2021-Jan-10更新的Multiwfn 3.8(dev)版。

1 理論方法和基組、贗勢的選取

1.1 理論方法

本文只涉及最常用的DFT計算。過渡金屬配合物的泛函測試文章很多，但算鑭系錒系用什么泛函最合適沒有特別系統全面的測試。PBE0是值得優先考慮的，在不少文章里用于算鑭系配合物，比如Inorg. Chem., 58, 411 (2019)里用就PBE0結合SDD贗勢做了含Pr體系的計算。在SARC全電子基組的原文J. Chem. Theory Comput., 5, 2229 (2009)和Jorge 2-zeta全電子基組原文Chem. Phys. Lett., 643, 84 (2016)里，作者基于PBE0做全電子計算得到了挺好的結果。

PBE0不是唯一選擇，筆者在《簡談量子化學計算中DFT泛函的選擇》（http://www.shanxitv.org/272）中提到的那些可以算過渡金屬配合物的泛函也都可以嘗試用于鑭系配合物的計算，諸如BP86、TPSS、TPSSh等。一般體系計算非常常用的B3LYP不是上佳的選擇，雖然在不少文章中也有人拿它算鑭系。

鑭系錒系元素相對論效應很顯著，必須考慮相對論效應。其配合物可以用全電子基組結合相對論哈密頓（常見的有DKH2、DKH4、ZORA、X2C）做全電子相對論計算，也可以對鑭系錒系原子用考慮了相對論效應擬合的贗勢計算。在Gaussian中，對于這類體系的優化和振動分析一般應當基于贗勢計算，因為Gaussian沒有相對論哈密頓的解析導數，故這類任務極其耗時。

1.2 贗勢和贗勢基組的選擇

對贗勢缺乏了解的話，先看《談談贗勢基組的選用》（http://www.shanxitv.org/373）和《贗勢的函數形式以及在量子化學程序中定義的方式》（http://www.shanxitv.org/188）。另外，筆者在北京科音基礎量子化學培訓班（http://www.keinsci.com/workshop/KBQC_content.html）里有十分全面細致的關于贗勢的專題講解。對于計算鑭系錒系，首選Stuggart贗勢（亦稱SDD贗勢）。Stuttgart贗勢對鑭系錒系有大核和小核版本，在《詳解Gaussian中混合基組、自定義基組和贗勢基組的輸入》（http://www.shanxitv.org/60）中我專門介紹過。對于下文要計算的原子序號為67的Ho來說，大家去看Gaussian手冊的Pseudo關鍵詞部分（http://www.shanxitv.org/g09/k_pseudo.htm），可知Gaussian對Ho內置了MWB28、MWB56、MWB57、MHF56、MHF57五種Stuttgart贗勢。其中MHF的不用管，因為擬合贗勢時沒考慮相對論效應，結果根本沒法用，諸如算的配位鍵鍵長都明顯不合理。MWB28是以Wood-Boring方式考慮準相對論效應的相對論贗勢，是小核贗勢，把1s 2s 2p 3s 3p 3d共28個內核電子用贗勢代替了。MWB56和MWB57是大核贗勢，把1s 2s 2p 3s 3p 3d 4s 4p 4d 4f電子都贗化了。其中MWB56是專門給Ho(III)用的，Ho(III)相當于Ho丟了全部兩個6s電子和11個4f電子當中的一個，由于1s 2s 2p 3s 3p 3d 4s 4p 4d一共有46個電子，再加上剩下的10個4f電子，因此一共是56個電子被贗化了。MWB57是專門給Ho(II)用的，其此時的全部11個f電子都被贗化了。用大核贗勢的好處在于，由于在配合物中近簡并的4f軌道不需要被描述，因此SCF收斂明顯比較容易，而且相對于小核贗勢來說計算也更快。大核贗勢的缺點是精度一般不如小核贗勢，而且可移植性差，不適合研究配位情況顯著改變的化學過程（如涉及到配位鍵形成和斷裂的反應、異構化），還需要自己恰當判斷原子的價態。小核贗勢用起來明顯更為穩妥、普適，但缺點是耗時更高，而且由于4f電子的近簡并導致SCF極其難收斂（實際算過的人肯定都深有體會），這令耗時更高。我建議小核贗勢用在幾何優化結束后的單點能計算、各種屬性的研究（如計算激發態）、產生用于做波函數分析的波函數等場合（見《在贗勢下做波函數分析的一些說明》http://www.shanxitv.org/156），以及用于配位情況明顯改變的過程的研究。

贗勢和贗勢基組是兩碼事，Stuttgart贗勢有不同的與之兼容的描述價電子的贗勢基組。對于DFT計算且要求不太高時，就用Gaussian里自帶的Stuttgart贗勢標配的贗勢基組即可。如果想讓結果更好，對鑭系可以用def2-TZVP或更高級的def2-QZVP，它定義了贗勢基組部分，對應的贗勢是Stuttgart的MWB28小核贗勢。在撰文時def2系列對于錒系沒有定義，但可以用對錒系有定義的def系列，它也是定義了贗勢基組部分并結合Stuttgart小核贗勢。注意Gaussian至少截止到撰文時最新的G16 C.01仍沒有內置鑭系錒系的def/def2基組，必須去Turbomole基組庫當中拷，見《在線基組和贗勢數據庫一覽》（http://www.shanxitv.org/309）。Lanl2贗勢+標配基組支持La、U、Np、Pu，但用得很少，沒必要考慮。CRENBL大核贗勢也支持鑭系錒系，但如今鮮有人用。

1.3 全電子相對論計算的基組選擇

Gaussian支持DKH2和DKH4標量相對論哈密頓計算（另外還支持的DKH0和RESC太爛，這里就不提了），DKH2非常常用，比起非相對論計算耗時僅高一丁點。DKH4在原理上更精確，耗時比DKH2也就多個幾分之一。對這兩種情況的基組建議：
? 用DKH2的情況：我建議對鑭系元素用Neese搞的SARC基組，這是很好的3-zeta檔次的基組，不特別昂貴結果又挺好。SARC有針對DKH2和ZORA優化的兩種版本，顯然當前情況要用前者。想要對鑭系結果更好還可以用SARC2的DKH2版，是4-zeta檔次的。二者在BSE上都有，不知道BSE是啥的話看《在線基組和贗勢數據庫一覽》（http://www.shanxitv.org/309）。SARC對前四周期沒有定義，因此對于配體部分需要用其它基組，非常適合的是用Neese他們搞的針對DKH2重收縮的def2系列基組，但這沒有公開發表，而只是內置于他們的ORCA程序中，在ORCA程序中用PrintBasis關鍵詞打印出來定義再整理成Gaussian的格式雖然可以用，但稍麻煩，BSE上也沒法直接獲取。另一個對配體可以考慮的是Jorge專為DKH2優化的一套基組，從DZ到6Z檔次都有，DZ和TZ版覆蓋1~103號元素，BSE上搜Jorge即可下載到定義。如果你是做后HF計算，配體可以用帶-DK后綴的給DKH2優化的Dunning相關一致性基組。
? 用DKH4的情況：我建議用Weigend等人（def2系列基組的作者）提出的x2c-系列基組，涵蓋前六個周期所有元素（包括鑭系），在BSE上可以下載到基組定義，但在Turbomole基組庫中種類最全。此基組專門給X2C相對論哈密頓計算而設計，用于精度也很高的DKH4計算也完全可以，此基組原文測試發現結合X2C還是DKH4誤差差不多。x2c-有用于標量相對論計算（后綴為all）和二分量相對論計算（后綴為all-2c）的兩類版本，后者更大，對于DKH4標量相對論計算用前者就夠了。x2c-和def2系列一樣有不同尺寸的版本，比如x2c-SVPall、x2c-TZVPall、x2c-QZVPall等。

相對論量子化學的原理和全電子相對論計算的各種相關知識我在北京科音（http://www.keinsci.com）的高級量子化學培訓班里會很詳細展開講，并全面盤點全電子相對論計算可以用的所有基組，本文就不再多說了。

下面就演示具體計算例子12-冠-4-五水合鈥(III)陽離子，涉及到的所有文件都可以在http://www.shanxitv.org/attach/581/file.rar下載。

2 構建結構

作為例子要計算的12-冠-4-五水合鈥(III)陽離子在劍橋結構數據庫(CSD)里面有，不用我們自己畫。它對應GINREA條目的陽離子部分，除此之外還有氯陰離子、游離的水分子，本文我們不考慮后兩者，計算在真空下當做孤立體系來進行。

進入CSD搜索頁面https://www.ccdc.cam.ac.uk/structures/，Identifier(s)里輸入CSD識別碼GINREA，就可以進入下面的頁面

我們要導出其坐標。沒必要先下載cif文件然后再提取分子，直接導出網頁中顯示的結構即可。做法是在3D窗口中點右鍵，選下面的選項

之后會出現一個文本框，把里面的內容復制到一個文本文件里，改名為GINREA.mol。

用GaussView打開這個mol文件，看到下圖。由于GINREA條目是是X光衍射測定的結構，氫的位置一般沒法準確確定或完全不能確定，水上只有氧原子。相關知識見《實驗測定分子結構的方法以及將實驗結構用于量子化學計算需要注意的問題》（http://www.shanxitv.org/569）。

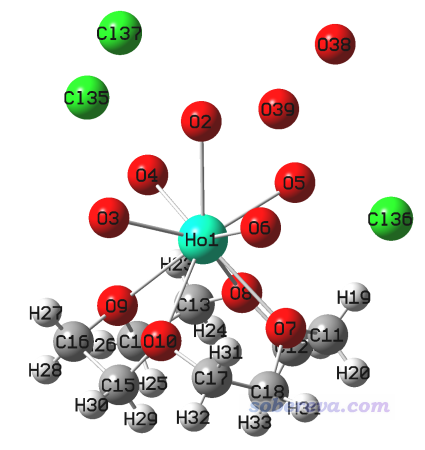
把三個氯離子，以及沒有配位的兩個水的氧原子都刪掉，然后點擊GaussView的加氫按鈕，給配位水的氧上面都點上兩個氫原子。如下所示

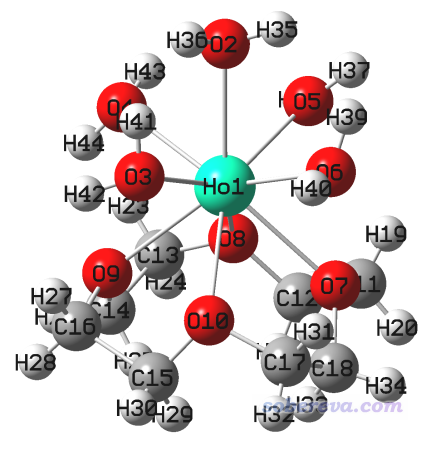
將當前結構保存為optfreq.gjf。

3 幾何優化+振動分析

這個配合物的自旋多重度取決于Ho(III)的10個4f電子的排布，可以為單重態、三重態、五重態。在幾何優化與振動分析過程中，按照前面的建議，我們用大核贗勢來做這一步，此時4f電子是被贗化的，所以Ho(III)上的價電子就只有將5s和5p軌道都占滿的8個電子了，而配體部分都是閉殼層電子結構，因此計算時應當設成單重態來算。

將optfreq改寫為如下內容。

%chk=optfreq.chk
#p pbe1pbe/genecp em=gd3bj int=fine opt freq
<-- 空行
GINREA
<-- 空行
3 1
[坐標部分]
<-- 空行
C O H
6-31G* <-- 此例對精度要求不高，對配體用低保基組
****
Ho
MWB56 <-- 用大核Stuttgart贗勢標配的贗勢基組
****
<-- 空行
Ho
MWB56 <-- 用大核Stuttgart贗勢
<-- 空行
<-- 空行

用int=fine是因為PBE0對于DFT積分格點不敏感，用Gaussian 16默認的int=ultrafine積分格點太浪費了。這里加了DFT-D3(BJ)校正，實際上對這個體系的優化沒必要加，但加了也沒壞處，并且對于以后研究弱相互作用、金屬-有機反應能、配體結合能等問題的精度還有改進，故索性就在本文所有計算中都加了。相關信息見《談談“計算時是否需要加DFT-D3色散校正？”》（http://www.shanxitv.org/413）、《亂談DFT-D》（http://www.shanxitv.org/83）。

用Gaussian計算此任務，得到optfreq.out，最終結構如下，沒有虛頻

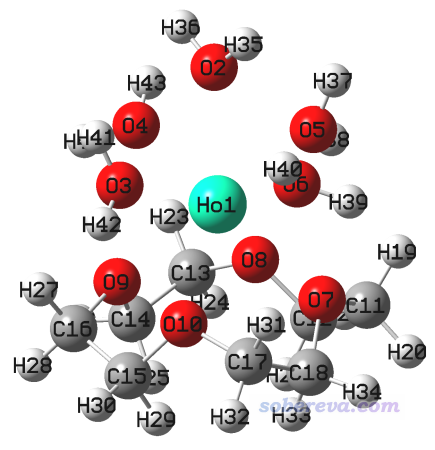
然后把這個結構保存成下一步的輸入文件，名為SP_stableopt.gjf。

4 單點計算+波函數穩定性測試

下面演示怎么做單點計算來得到更好的能量。為此，把贗勢改為小核贗勢，如Gaussian手冊pseudo關鍵詞所述，直接寫SDD對于Ho就等同于用了MWB28贗勢。配體部分基組從之前的6-31G*增大到6-311G*。當然了，當前的基組仍只是中等檔次，想要更好的結果建議對所有原子都用def2-TZVP（基組名直接寫def2TZVP即可，不用genecp了）。

這次由于4f電子被顯式地考慮了，我們也需要明確考慮此體系的自旋多重度問題。如果你拿不準，就把所有可能的自旋多重度，即單重態、三重態、五重態都算一下試試，看誰的能量低。也不需要非得等到SCF完全收斂后再對比能量，比如能量收斂到0.00001 a.u.了就可以停了，再迭代下去也不會改變太多，這種收斂精度下的不同自旋態的能量差就已經能說明問題了。實際上像當前這樣的配體不計算也能估計到是高自旋的，即10個f電子里7個alpha、3個beta，因此是7-3+1=五重態。

由于鑭系錒系配合物容易收斂到不穩定波函數，因此強烈建議加上stable=opt，使得程序對SCF收斂后的波函數進行檢測，如果不穩定的話則自動試圖優化到穩定波函數。《談談片段組合波函數與自旋極化單重態》（http://www.shanxitv.org/82）中有更多相關討論。

我們把SP_stableopt.gjf的內容改成下面這樣，然后運行。

%chk=SP_stableopt.chk
#p PBE1PBE/genecp em=gd3bj int=fine stable=opt
<-- 空行
opted
<-- 空行
3 5
[坐標部分]
<-- 空行
C O H
6-311G*
****
Ho
SDD
****
<-- 空行
Ho
SDD
<-- 空行
<-- 空行

由輸出文件SP_stableopt.out可見，在第一次做SCF的時候，跑了多達74輪SCF才收斂。小核贗勢算鑭系錒系配合物SCF收斂普遍就是很難，跑到一百多輪才收斂也很常見。雖然我很反感加大Gaussian本來默認得就已經很大的SCF迭代次數上限的行為，但算鑭系錒系配合物的時候倒是可以總是加個SCF=maxcyc=200。在《解決SCF不收斂問題的方法》（http://www.shanxitv.org/61）里我已經全面列舉了解決SCF不收斂問題的方法，其中很多方法對其它體系容易見效，但對鑭系錒系配合物仍然不好使。對于只需要得到DFT單點能的情況，如果在SCF迭代過程后期由于很微小的震蕩就是死活不收斂，不得已時也可以加上SCF=conver=6放寬收斂限兩個數量級。但對于G16來說（至少截止到撰文時最新的G16 C.01而言），收斂不到默認的tight收斂限（相當于SCF=conver=8）的話就不給做涉及能量導數的任務、TDDFT，甚至連我們當前想做的波函數穩定性測試也沒法做，這個要求是G16很惡心的一點。

當前這個計算SCF能直接收斂已經挺幸運了，之前筆者還遇到幾乎用了所有方法SCF都死活收斂不到默認收斂限的情況。后來總算發現有一個做法奏效，就是先用HF成分很高（50%）的BHandHLYP計算，由于HF成份很高所以gap大，對于前線軌道近簡并體系的SCF比起PBE0容易收斂不少，然后在PBE0計算的時候讀取BHandHLYP收斂的波函數當初猜，最終可算是收斂了。

不要因為SCF收斂了就高興得太早，當前波函數穩定性測試有這樣的輸出：
Eigenvector   1: 5.002-A    Eigenvalue=-0.0080098 <S**2>=6.004
     65B -> 91B       -0.13744
     67B -> 91B        0.11409
     70B -> 92B        0.52213
     71B -> 90B       -0.56619
     72B -> 91B        0.55567
The wavefunction has an internal instability.
因此沒收斂到穩定波函數上。于是按照stable=opt關鍵詞的要求，Gaussian自動試圖優化出穩定的波函數，這個過程非常耗時，而且也有出現不收斂的可能。完成后程序提示
Eigenvector   1: 5.002-A    Eigenvalue= 0.0007336 <S**2>=6.004
     70B -> 91B        0.29385
     70B -> 93B       -0.44577
     71B -> 91B        0.15865
     71B -> 93B        0.11464
     72B -> 90B        0.57426
     72B -> 92B       -0.52623
The wavefunction is stable under the perturbations considered.
即波函數穩定了。最終chk文件SP_stableopt.chk里記錄的就是穩定的波函數了，最后輸出的能量-1944.2616578也是可以用的了，這比起第一次SCF收斂后得到的-1944.25769973低了10.4 kJ/mol。

順帶一提，從上面第一次波函數穩定性測試輸出的以三行上可以了解到為什么波函數不穩定的一些端倪，這三項是系數絕對值最大的三個（如果你做TDDFT計算，也會發現第一激發能是負值，并且下面這三種軌道躍遷的系數絕對值很大）。
     70B -> 92B        0.52213
     71B -> 90B       -0.56619
     72B -> 91B        0.55567
如果你拿沒用stable=opt關鍵詞做當前任務得到的chk文件去看軌道，會發現beta的70、71、72是三個占據的4f軌道，beta的90、91、92是三個非占據的4f軌道，因此波函數不穩定的原因可能是4f殼層上的beta電子占據方式有問題。4f的alpha電子顯然不可能有類似這種問題，因為7個alpha 4f電子已經把7個alpha軌道都占滿了。

還值得一提的是，SP_stableopt.out中優化出來的穩定波函數的<S**2>是6.0037，這和5重態的理想值6.0幾乎嚴格相同，這體現出當前體系自旋極化特征很弱，即alpha和beta占據軌道的空間分布幾乎完全匹配。

5 一些相關分析

將SP_stableopt.chk用formchk轉換為SP_stableopt.fchk，就可以用Multiwfn（http://www.shanxitv.org/multiwfn）做各種各樣的波函數分析了。Multiwfn的相關信息看《Multiwfn FAQ》（http://www.shanxitv.org/452）和《Multiwfn入門tips》（http://www.shanxitv.org/167），這里就隨便舉幾個簡單分析例子，都是研究此類體系在文獻中常涉及的。

當前體系是五重態，alpha電子比beta多4個，多的這4個電子在哪里？可以用Multiwfn做一下布居分析。啟動Multiwfn后載入SP_stableopt.fchk，然后依次輸入
7 //布居分析
5 //Mulliken分析
1 //輸出Mulliken布居和原子電荷
從輸出中可見如下信息。由Spin pop.（自旋布居）那一列可見，4個alpha電子幾乎完全定域在Ho的4f軌道上，在其它軌道或其它原子上的自旋布居可以忽略不計，這和我們期望的完全一致。如果不了解自旋布居的話，看《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》（http://www.shanxitv.org/353）。
Population of each type of angular moment atomic orbitals:
    Atom    Type   Alpha pop.   Beta pop.    Total pop.   Spin pop.
    1(Ho)    s      2.09443      2.09001      4.18443      0.00442
             p      6.02215      6.01624     12.03840      0.00591
             d      5.21226      5.19202     10.40427      0.02024
             f      7.02724      3.04892     10.07616      3.97832
             g      0.00730      0.00744      0.01474     -0.00015
    2(O )    s      1.94896      1.94910      3.89806     -0.00015
             p      2.50701      2.50728      5.01430     -0.00027
...略

再往下還能看到Mulliken原子電荷，即Atomic charge那一列。可見Ho明顯帶正電荷，五個配位水的氧帶的負電荷量比冠醚的氧帶的更多。如果用Multiwfn計算Hirshfeld、ADCH（原子偶極矩校正的Hirshfeld電荷）、CM5等其它流行的原子電荷也可以得到相同的結論。
Population of atoms:
    Atom      Alpha pop.   Beta pop.    Spin pop.     Atomic charge
    1(Ho)     20.36337     16.35463      4.00875         2.28200
    2(O )      4.46188      4.46230     -0.00042        -0.92418
    3(O )      4.46066      4.46161     -0.00095        -0.92226
    4(O )      4.46283      4.46346     -0.00063        -0.92628
    5(O )      4.46074      4.46169     -0.00095        -0.92242
    6(O )      4.46282      4.46344     -0.00062        -0.92625
    7(O )      4.23562      4.23647     -0.00085        -0.47208
    8(O )      4.23750      4.23856     -0.00106        -0.47606
    9(O )      4.23556      4.23640     -0.00085        -0.47196
   10(O )      4.23753      4.23859     -0.00106        -0.47612
...略

鑭系元素在配合物中多為三價（氧化態為3），還有少見一些的二價、四價、五價，在Inorg. Chem., 58, 411 (2019)中還研究了一價的情況。前面我們將此體系中的Ho視為了最常見的三價并用了相應的大核贗勢，但視為三價是否一定合理？這里按照《使用Multiwfn通過LOBA方法計算氧化態》（http://www.shanxitv.org/362）所述的方法進行檢驗。按照文中的過程計算，采用50%作為判斷閾值，得到如下輸出
Oxidation state of atom   1(Ho) : 3
Oxidation state of atom   2(O ) : -2
Oxidation state of atom   3(O ) : -2
Oxidation state of atom   4(O ) : -2
Oxidation state of atom   5(O ) : -2
Oxidation state of atom   6(O ) : -2
...略
可見Ho確實可以視為是三價的。

Atoms-in-molecules (AIM)理論是非常流行的考察原子間相互作用的一套理論，相關信息見《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）和《使用Multiwfn做拓撲分析以及計算孤對電子角度》（http://www.shanxitv.org/108）中的相關介紹以及《AIM學習資料和重要文獻合集》（http://bbs.keinsci.com/thread-362-1-1.html）中的大量資料。對當前的體系，按照《使用Multiwfn+VMD快速地繪制高質量AIM拓撲分析圖（含視頻演示）》（http://www.shanxitv.org/445）中的做法繪制的AIM拓撲圖像如下，其中將隨便選的一個Ho-O鍵的鍵臨界點（BCP）的幾個屬性標注上了。

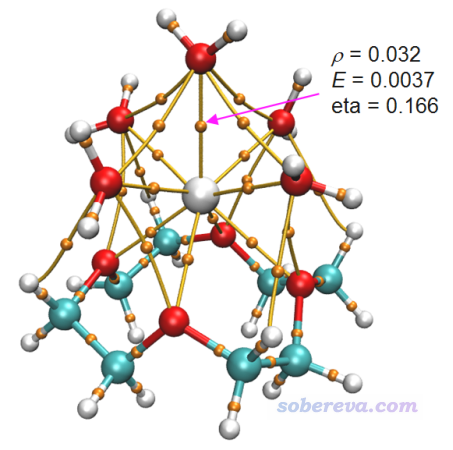
化學鍵是共價作用還是非共價作用在《Multiwfn支持的分析化學鍵的方法一覽》中筆者介紹過怎么根據BCP的屬性判斷。由于這個BCP的能量密度大于0，而且eta指數小于1，所以可以被認為是非共價作用為主，而共價作用特征非常微弱。讀者也可以用Multiwfn算一下Mayer鍵級，會發現Ho-O的鍵級值非常小，也體現出Ho-O鍵更類似于離子鍵，結合主要靠的是帶顯著正電荷的Ho與帶顯著負電荷的氧之間的靜電吸引作用。

RDG方法是非常流行的圖形化展現非共價相互作用的方法，因此配體之間的弱相互作用，以及配位氧與Ho的非共價作用都應當能被RDG方法所展現，原理和繪制操作詳見《使用Multiwfn圖形化研究弱相互作用》（http://www.shanxitv.org/68）、《用Multiwfn+VMD做RDG分析時的一些要點和常見問題》（http://www.shanxitv.org/291）和視頻演示《使用Multiwfn做NCI分析展現分子內和分子間弱相互作用》（https://www.bilibili.com/video/av71561024）。當前體系的著色的RDG等值面圖如下所示，可見位阻作用區域（紅色），配體間較顯著的范德華作用區域（綠色），以及Ho與配位氧之間的明顯的吸引作用都被展現了出來。

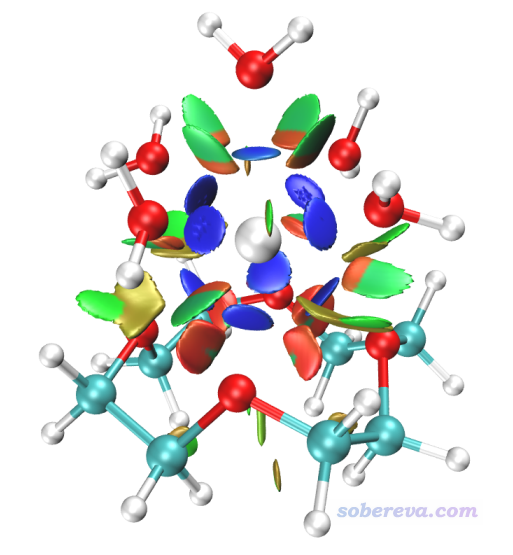
此體系中與Ho配位的原子非常多。如果想簡單快速可靠地判斷配位數的話，可以利用Multiwfn里的一個專門的功能。啟動Multiwfn，然后載入SP_stableopt.gjf（用這個功能的輸入文件只要有坐標信息即可，載入fchk當然也可以），然后輸入
100
9
[直接按回車]
然后可以看到下面的輸出，即Ho的配位數是9，很合乎我們的直覺。這個功能的判斷原理介紹見Multiwfn手冊3.100.9節
1 Ho Sum of connectivity: 12.2412   Sum of integer connectivity: 9
2 O   Sum of connectivity: 2.9604   Sum of integer connectivity: 3
3 O   Sum of connectivity: 2.9800   Sum of integer connectivity: 3
4 O   Sum of connectivity: 2.9757   Sum of integer connectivity: 3
...略

電荷分解分析(CDA)對于研究中心金屬和配體的軌道相互作用很有價值，感興趣者建議按照《使用Multiwfn做電荷分解分析(CDA)、繪制軌道相互作用圖》（http://www.shanxitv.org/166）所述進行分析。

最后，用Multiwfn基于optfreq.out繪制一下這個體系的紅外光譜，方法和細節見《使用Multiwfn繪制紅外、拉曼、UV-Vis、ECD、VCD和ROA光譜圖》（http://www.shanxitv.org/224），這里就不再累述過程了，得到的圖像如下所示。當前體系用了混合基組，沒有嚴格的頻率校正因子可用，因此在Multiwfn里繪圖時就用了占原子最多的6-31G*基組在PBE0下的基頻校正因子，CCCDBD上給的值是0.95，相關知識見《談談諧振頻率校正因子》（http://www.shanxitv.org/221）。

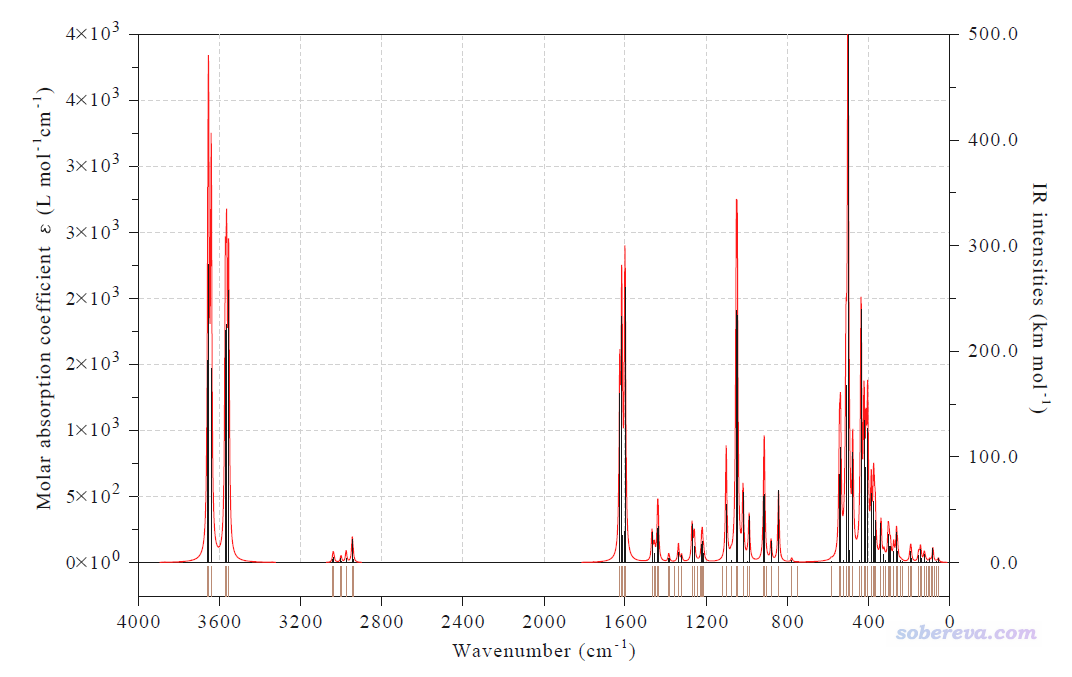
6 全電子標量相對論計算

下面演示一下用DKH4相對論哈密頓結合很好的x2c-TZVPall全電子基組做計算，用當前這種級別計算比之前用小核贗勢的那個例子精度明顯更高，但也明顯更昂貴，不過如果有個像樣的雙路服務器的話毫無壓力。還是用之前優化過的結構，改寫成下面這樣，對應本文文件包里的SP_stableopt_DKH4_x2c-TZVPall.gjf。此處DKHSO代表做DKH4標量相對論計算。x2c-TZVPall基組定義是從BSE上拷來的。照舊我們還是要做波函數穩定性檢測，并當發現不穩定時試圖優化出穩定的波函數。

%chk=SP_stableopt_DKH4_x2c-TZVPall.chk
#p PBE1PBE/gen em=gd3bj int(DKHSO,fine) stable=opt
<-- 空行
DKH4 with x2c-TZVPall
<-- 空行
3 5
[坐標部分]
<-- 空行
H     0
S    3   1.00
     34.0613410              0.60251978D-02
      5.1235746              0.45021094D-01
      1.1646626              0.20189726
S    1   1.00
      0.32723041             1.0000000
S    1   1.00
      0.10307241             1.0000000
P    1   1.00
      0.8000000              1.0000000
****
C     0
S    6   1.00
13602.8672210             -0.37777522999D-03
   2025.6373438             -0.23576500983D-02
    463.91231001            -0.11596012028D-01
    130.82215199            -0.46115805966D-01
     42.923923821           -0.14105167104
     15.581525131           -0.31080969741
S    2   1.00
      6.2892392533          -0.15604284118
      2.6572302404          -0.96370811902D-01
S    1   1.00
      0.57807742401          1.0000000000
S    1   1.00
      0.22989985704          1.0000000000
S    1   1.00
      0.95160774246D-01      1.0000000000
P    4   1.00
     34.707038490            0.53684294999D-02
      7.9558987851           0.35952788969D-01
      2.3791715536           0.14232010989
      0.81439359487          0.34277842056
P    1   1.00
      0.28897779004          1.0000000000
P    1   1.00
      0.10058968205          1.0000000000
D    1   1.00
      1.0970000000           1.0000000000
D    1   1.00
      0.31800000000          1.0000000000
F    1   1.00
      0.76100000000          1.0000000000
****
O     0
S    6   1.00
27129.7236970             -0.38412016008D-03
   4027.0930191             -0.21890968046D-02
    922.41748966            -0.10403684068D-01
    260.46373931            -0.41183208891D-01
     85.461818612           -0.12812329149
     31.032450616           -0.29445956566
S    2   1.00
     12.392742851           -0.16362839154
      5.1198045492          -0.10697361899
S    1   1.00
      1.1764031300           1.0000000000
S    1   1.00
      0.46546138443          1.0000000000
S    1   1.00
      0.18500871202          1.0000000000
P    4   1.00
     63.347523551            0.61381103984D-02
     14.624684698            0.42042980032D-01
      4.4491599423           0.16170252002
      1.5277866789           0.35706070979
P    1   1.00
      0.52943458369          1.0000000000
P    1   1.00
      0.17479105448          1.0000000000
D    1   1.00
      2.3140000000           1.0000000000
D    1   1.00
      0.64500000000          1.0000000000
F    1   1.00
      1.4280000000           1.0000000000
****
Ho     0
S    10   1.00
30665374.1250000             0.66695471846D-03
4895948.2993000              0.19386599630D-02
1050837.3977000              0.47658287331D-02
266278.7640400              0.11250169585D-01
76845.5599300              0.26218913848D-01
24489.0709730              0.60786144743D-01
   8459.8494420              0.13512331601
   3106.3269192              0.27484876838
   1177.0152475              0.40496960964
    449.39639997             0.26738683755
S    5   1.00
   7931.4428438             -0.65012808265D-02
   2062.9540658             -0.41639923229D-01
    758.91395632            -0.89618339118D-01
    212.99194519             0.24193617465
     62.170129827            0.41282007533
S    1   1.00
    111.79560111             1.0000000000
S    1   1.00
     20.085848751            1.0000000000
S    1   1.00
     10.408086826            1.0000000000
S    1   1.00
      5.8445952034           1.0000000000
S    1   1.00
      2.8986852103           1.0000000000
S    1   1.00
      0.89005737804          1.0000000000
S    1   1.00
      0.40024972043          1.0000000000
S    1   1.00
      0.71739741553D-01      1.0000000000
S    1   1.00
      0.29402884127D-01      1.0000000000
P    8   1.00
228101.0193500              0.39863207230D-03
35137.1587650              0.19960538599D-02
   8359.3029774              0.89323482634D-02
   2561.2112267              0.35889379966D-01
    910.46609243             0.12249794321
    361.78057659             0.30388576399
    153.15183730             0.45389599787
     65.520483330            0.25257470359
P    5   1.00
   4474.3792479              0.56389120441D-03
    281.65682206            -0.20022067678D-01
     49.036380826            0.30557667261
     24.143269547            0.60828263889
     11.576198496            0.29432830931
P    4   1.00
    301.86445103            -0.35271226558D-02
      7.8265880455           0.49062342009
      3.9718699429           0.58993778863
      2.0434455994           0.22431999653
P    3   1.00
      3.0206586049          -0.45894143382D-01
      1.5399070185           0.22608423905
      0.68956994737          0.65278925439
P    1   1.00
      0.27321141746          1.0000000000
P    1   1.00
      0.94210833607D-01      1.0000000000
P    1   1.00
      0.38623978525D-01      1.0000000000
D    6   1.00
   1844.7814682              0.27871573414D-02
    527.76862601             0.21502263613D-01
    198.48802324             0.97398372591D-01
     84.848163250            0.27301874739
     38.605610951            0.44077530105
     18.126277426            0.31353513996
D    3   1.00
     24.327558659            0.43274993682D-01
     12.866617783            0.19755692505
      7.1130943232           0.39095056285
D    1   1.00
      3.6185615081           1.0000000000
D    1   1.00
      1.6037544992           1.0000000000
D    1   1.00
      0.47027114517          1.0000000000
D    1   1.00
      0.12774649728          1.0000000000
D    1   1.00
      0.34700000000D-01      1.0000000000
F    5   1.00
    171.69748056             0.49321674004D-02
     58.758874336            0.33460197436D-01
     24.181400080            0.11575293621
     10.879946094            0.24114731797
      5.0028781306           0.31886369645
F    1   1.00
      2.2593141386           1.0000000000
F    1   1.00
      0.95842954854          1.0000000000
F    1   1.00
      0.35729266508          1.0000000000
G    1   1.00
      0.49850000000          1.0000000000
****
<-- 空行
<-- 空行

此任務第一次SCF收斂后得到的波函數也和之前用小核贗勢的時候一樣，提示不穩定，然后優化出了穩定的波函數。

大家如果做Mulliken布居分析，和之前一樣會發現是4個alpha單電子都在Ho上，但是Mulliken電荷如今是1.374，用小核贗勢時是2.282，看似相差不小，這倒不是因為電子結構相差多少，而主要在于Mulliken電荷對基組的敏感性很強，這點在《原子電荷計算方法的對比》（http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml）一文中我專門說過。如果用對基組敏感性很弱的Hirshfeld、ADCH等電荷，會發現兩種情況差不多。對當前全電子波函數算Mayer鍵級，雖然Ho-O的鍵級整體比之前用贗勢的情況有明顯增大，現在在0.3左右，但相對于一般的共價鍵的情況來說數值依然很小，這一方面是算出來的電子結構確實有些不同，另一方面是Mayer鍵級對基組也比較敏感。對當前波函數做AIM拓撲分析，BCP處的屬性相對于之前有一些定量改變，但Ho(III)-O相互作用主體是非共價作用的結論還是不變的。