使用Multiwfn做空穴-電子分析全面考察電子激發特征
2022-Mar-1注:本文介紹的功能已支持結合CP2K做TDDFT計算研究周期性體系的電子激發,參見《使用CP2K結合Multiwfn對周期性體系模擬UV-Vis光譜和考察電子激發態》(http://www.shanxitv.org/634)。
使用Multiwfn做空穴-電子分析全面考察電子激發特征
文/Sobereva @北京科音
First release: 2018-Aug-31 Last update: 2023-Mar-18
1 前言
空穴-電子(hole-electron)分析是Multiwfn程序支持的一種非常強大、極為實用的考察電子激發特征的一套方法,它將電子激發過程描述為“空穴→電子”,從而可以以圖形化的方式非常直觀地考察電子從哪離開、到哪去,是局域激發、整體激發、電子轉移激發還是雜化特征的激發。還可以定量考察電子轉移距離、空穴與電子的分離程度、原子或片段對電子激發的貢獻、空穴與電子的庫侖吸引能等等。此分析可以用于CIS、TDHF、TDA-DFT和TDDFT方法做的電子激發任務。空穴-電子分析的最初靈感來自于筆者和同行鐘成的討論,并早在2013年就已經在Multiwfn中實現了,之后又經過不斷完善和擴展。到2022年已經有幾百篇已發表的SCI文章使用了空穴-電子分析,如Nature Catalysis (2023) DOI: 10.1038/s41929-023-00972-x, Nature Materials, 19, 1332 (2020)、J. Phys. Chem. Lett., 9, 4857 (2018)、J. Phys. Chem. C, 121, 8091 (2017)、J. Mater. Chem. C, 5, 5214 (2017)等,以及筆者的Phys. Chem. Chem. Phys., 24, 7466 (2022)等。在筆者不少博文里也涉及了空穴-電子分析,如《圖解電子激發的分類》(http://www.shanxitv.org/284)、《在Multiwfn中通過IFCT方法計算電子激發過程中任意片段間的電子轉移量》(http://www.shanxitv.org/433)等。
本文撰寫的目的是系統性地介紹一下空穴-電子分析,使更多人能了解到此方法的重要性,并充分應用于自己的研究當中。凡是仔細、認真閱讀本文的讀者,必定會感受到空穴-電子分析的強大。即便之前已經長期使用空穴-電子分析的人也請仔細閱讀本文,其中涉及了很多技巧,并介紹了空穴-電子分析框架在最新的Multiwfn中加入的各種新特征和相對于老版本的變動。筆者未來會專門寫一篇介紹空穴-電子分析的論文發表,在此文發表之前,如果你的研究中用了空穴-電子分析方法,請務必在引用Multiwfn原文的同時也引用筆者的此文:Carbon, 165, 461-467 (2020) DOI: 10.1016/j.carbon.2020.05.023。在這篇文章中筆者應用了空穴-電子分析研究了18碳環體系,并且在補充材料里對空穴-電子分析的原理做了簡要介紹,并與其它可以分析空穴、電子分布的方法做了對比。
除了空穴-電子分析外,本文對目前已經被不少文章使用的衡量電子激發特征的Λ和Δr指數的原理、與空穴-電子分析的關系以及在Multiwfn中的計算方法也作了介紹。看過本文后會明白這些指標已經沒有什么存在價值了,完全可以被空穴-電子分析框架里定義的更好的指標所取代。
本文內容對應于Multiwfn官網上的最新版本,如果發現本文內容或情況和你手里的Multiwfn不符,請先更新至最新版本。Multiwfn可以在其主頁http://www.shanxitv.org/multiwfn上免費下載。如果不了解Multiwfn,強烈建議參看《Multiwfn入門tips》(http://www.shanxitv.org/167)和《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)。除本文介紹的方法外,Multiwfn還支持一大堆極具價值的激發態分析方法,在此文里有匯總介紹,很建議一看:《Multiwfn支持的電子激發分析方法一覽》(http://www.shanxitv.org/437)。
2 空穴-電子分析的原理
空穴-電子分析原理的詳細介紹參看Multiwfn手冊3.21.1.1節。本節只是做一些基本性的介紹,有看不明白的請結合手冊看。
2.1 電子激發過程中空穴和電子的定義
對于CIS、TDHF、TDA-DFT和TDDFT,激發態波函數通過單激發組態函數的線性組合來描述,對這些方法不了解的話可參看《亂談激發態的計算方法》(http://sobereva.com/265)。對于CIS和TDA-DFT,每個組態函數各有個系數w;對于TDHF、TDDFT,每個組態函數既可作為激發組態而擁有系數w,也可以作為去激發組態而擁有系數w',這點在Multiwfn手冊3.21節開頭特意介紹了。經過推導,對于TDHF/TDDFT,空穴和電子的表達式可寫為以下形式。如果是CIS、TDA-DFT,則沒有w'那部分。
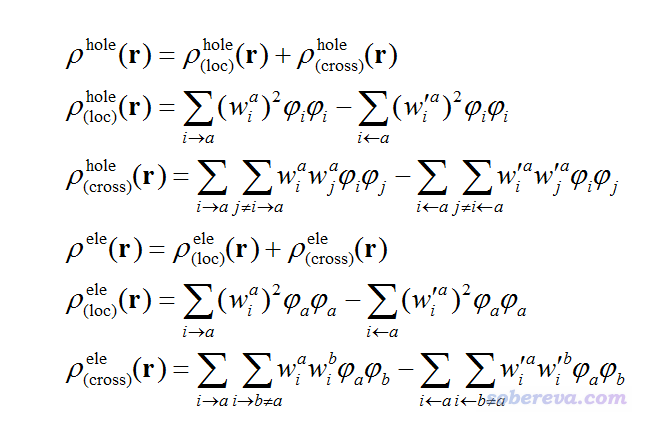
上式中,r是坐標矢量,φ是軌道波函數,i或j是占據軌道標號,a或b是空軌道標號。因此諸如∑i→a代表循環每一個激發組態,而∑i←a代表循環每一個去激發組態。空穴分布ρhole和電子分布ρele都分為局域項(local term)和交叉項(cross term)兩部分。局域項一般占主導,體現組態函數自身的貢獻,而交叉項也不可忽略,否則定量不準,它體現組態函數之間的耦合對空穴和電子分布的影響。
“空穴”和“電子”這兩個詞并不是Multiwfn里的空穴-電子分析獨創的,這兩個詞是抽象的概念,具體怎么定義并不唯一,應該說上面的這種定義是非常理想的,它滿足合理的空穴、電子定義所理應滿足的要求,即空穴和電子在全空間中積分值都為1(對應一個電子),而且處處為正。因此,上述方式定義的“空穴”的分布完美地描述了被激發的電子從哪里走,而“電子”的分布完美地描述被激發的那個電子去了哪。
實際上,倘若某個電子激發可以完美地由某一對軌道躍遷i→a所描述,換句話說這個組態函數的貢獻恰為100%(怎么算貢獻看《電子激發任務中軌道躍遷貢獻的計算》http://sobereva.com/230),那么φi和φa就可以直接理想地分別作為空穴和電子。而上面方式定義的空穴和電子,則分別相當于|φi|^2和|φa|^2的,可以視為是i和a軌道對應的電子密度(假設這倆軌道都是單占據情況)。因此,上面定義的電子和空穴是沒有相位信息的,因為對軌道波函數求了模方。由于實際算出來的電子激發態總是由很多組態函數共同參與,沒有哪一對軌道躍遷可以絕對完美地描述電子激發,因此為了能充分描述這種情況的電子和空穴,筆者和合作者才創造了上述電子和空穴的具體定義,它把所有軌道躍遷全都納入了考慮,可以理想、全面、充分地展現電子激發的特征。
很多人都知道NTO(自然躍遷軌道),筆者這兩篇文章也有過專門的介紹:《使用Multiwfn做自然躍遷軌道(NTO)分析》(http://sobereva.com/377)、《躍遷密度分析方法-自然躍遷軌道(NTO)簡介》(http://sobereva.com/91)。NTO通過對分子軌道進行酉變換,把分子軌道的躍遷轉化為NTO的躍遷來描述,此時很多情況電子激發就可以只用一個占據的NTO向一個非占據的NTO之間的躍遷來較理想的描述了,此時空穴和電子可以分別當做這兩個NTO的軌道波函數。NTO形式的空穴、電子和上述方式定義的空穴、電子各有利弊,NTO好處是保留了相位信息,這在討論的時候有時候更便于判斷空穴和電子對應什么類型軌道上,但是有很多情況,即便把電子激發變換成了NTO描述,還是沒有哪一對NTO的躍遷起到絕對主導作用(比如最大的一對NTO躍遷只貢獻80%),此時就必須用前面介紹的那種空穴、電子的定義,它對任何體系任何類型激發都是完美適用的。
2.2 空穴、電子分布的衍生量
基于上一節給出的Multiwfn中的空穴和電子的定義,可以定義幾個有用的衍生量。首先我們可以定義激發態與基態的密度差:Δρ=ρele-ρhole。這在下文簡寫為CDD (charge density difference)。
注意激發態密度有非弛豫(unrelaxed)和弛豫(relaxed)兩種。弛豫的激發態密度更為真實,與實際更為相符,但構造起來復雜耗時(需要利用Z-vector方法,耗時和算一次激發態受力相仿佛);而非弛豫密度構造比較簡單,利用參考態軌道和組態系數就可以直接得到,可以認為是實際激發態密度的一階近似,物理意義上可以理解為電子激發的一瞬間,電子結構還沒來得及發生重排時的激發態密度。關于弛豫和非弛豫密度的更多信息見http://bbs.keinsci.com/thread-5738-1-1.html。之所以在這里提一下弛豫和非弛豫激發態密度的區別,是因為如上方式利用空穴和電子分布計算的CDD對應的是非弛豫的激發態密度與基態的密度差,而使用Multiwfn手冊4.18.3節或《使用Multiwfn作電子密度差圖》(http://sobereva.com/113)中的方式給出的是弛豫的激發態密度與基態的密度差,二者的差異從下圖描述的一個體系的一種電子激發中可見一斑:
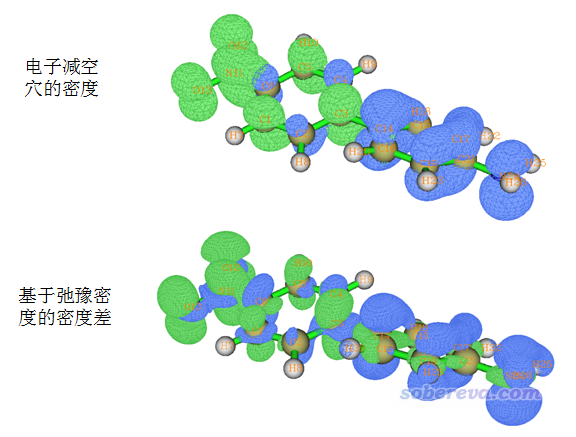
上面的CDD等值面圖中,綠色是正值部分,對應激發態相對于基態電子密度增加的地方,藍色是減小的地方。此圖所示的激發是具有電荷轉移特征的pi-pi*激發,因為從輸出的組態信息上看只有pi軌道參與。圖的上方是Multiwfn的空穴-電子分析給出的CDD,可見確實電子和空穴的等值面在共軛平面上都是有節面的,體現出純粹的pi激發特征。然而下方的基于弛豫的激發態密度得到的CDD圖上卻同時體現了一丁點sigma電子特征,這是因為pi電子被激發后,由于電子間的相互作用勢發生了改變,sigma軌道上的電子也出現了相應的響應。雖說基于非弛豫的激發態密度對應的CDD在原理上沒有基于弛豫的激發態密度的那么嚴格,但是對于討論電子激發特征是足夠的(而且還避免了電子密度進一步弛豫對圖像所產生的“干擾”)。平時我們會看到大量的計算文章中直接用MO或者NTO來討論電子激發特征,實際上這種討論方式相當于已經假定了激發態電子結構可以靠非弛豫密度充分地描述的這個前提了。
接下來,我們定義描述電子與空穴分布之間重疊的函數
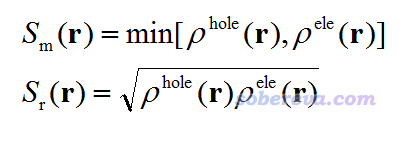
上面的Sm和Sr是描述重疊情況的兩種不同的定義,前者是取空穴和電子的最小值,后者是取幾何平均。兩種定義沒有絕對的優劣之分,都是合理的,容易證明Sr肯定大于Sm。我更傾向于用Sr這種定義,圖像效果更好,數學意義也稍微強一些,因此后文我們都用Sr函數來討論。通過繪制這兩個函數,我們可以清楚地了解到哪些區域電子和空穴重疊比較顯著。
2.3 分子軌道、原子、片段、基函數對空穴和電子的貢獻
筆者將分子軌道對空穴和電子的貢獻定義為以下形式,i和a是軌道標號。利用這樣的數據可以立刻知道哪些分子軌道對躍遷起到重要作用,并且便于定量分析討論
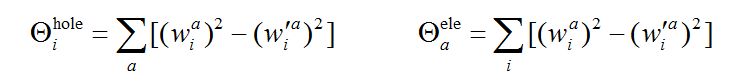
通過使用類似Mulliken方式的劃分,可以按照下式計算原子和基函數對空穴和電子的貢獻,A是原子標號,μ和ν是基函數標號,S是重疊矩陣,C是分子軌道展開系數矩陣
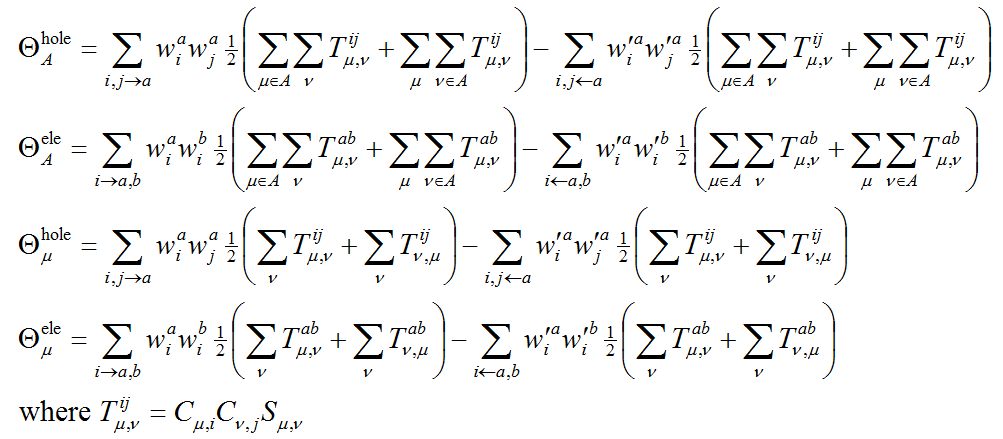
進一步,筆者定義了原子、片段對電子和空穴間差值(即CDD)的貢獻,以及在原子、片段空間內電子與空穴的重疊量:
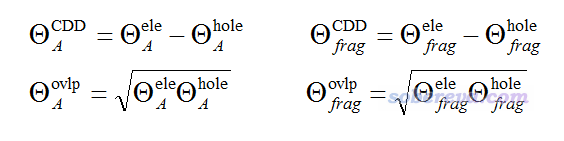
注意,以這種方式定義的原子/片段內的空穴與電子的重疊程度是不可加和的,比如在A原子和在B原子內重疊程度的加和不等于由A、B兩個原子組成的片段內的重疊程度。類似地,還可以計算對應某基函數的空穴和片段的重疊量,以及基函數對空穴和電子間差值的貢獻,就是把上面式子中原子標號改成基函數標號即可。
Multiwfn還直接支持通過Hirshfeld劃分計算原子/片段對空穴和電子的貢獻。
為了更便于考察,Multiwfn還支持把原子或片段對空穴、電子以及二者的重疊的貢獻通過填色圖形式展現,使得討論起來更為直觀,也便于在論文中把許多激發態的情況放到一起來對比,后面我們就會看到例子。
2.4 空穴和電子在全空間中分布特征的定量描述
為了便于通過一些定量數值衡量和討論電子激發特征,筆者定義了Sm和Sr指數,即Sm和Sr函數在全空間進行積分:
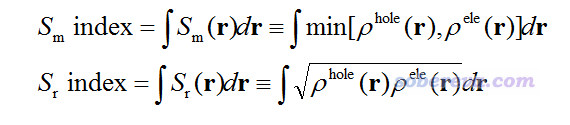
這兩個指數越大,說明空穴和電子的重疊程度越高;數值越小,說明空穴和電子的分離越顯著。Sr指數肯定大于Sm指數。這兩個指數的值域都是[0,1],1就代表空穴和電子完美重合,0就代表沒有絲毫交疊。
筆者還定義了衡量空穴和電子質心之間距離的D指數:
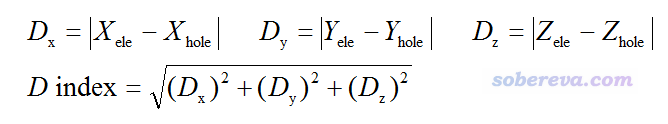
其中諸如X_hole指的是空穴的質心的X坐標,可以通過把ρhole函數乘上x坐標變量在全空間積分得到。所謂的質心就相當于函數整體分布的最中心、最具有代表性的那個點。
值得一提的是,激發態偶極矩相對于基態偶極矩的變化可以用空穴和電子質心的差值來直接計算。例如X分量的變化等于-(X_ele-X_hole),括號前頭有個負號是因為電子帶負電。
J. Chem. Theory Comput., 7, 2498 (2011)文章提出了基于密度差對電子激發特征進行分析的一系列指標,筆者發現這些指標也可以很好地挪用到空穴和電子特征的分析上(但很多指標的原始定義不理想或者缺乏普適性,我做了修改)。首先,對空穴和電子都可以定義σ,它的x,y,z三個分量相當于空穴或電子在x,y,z方向上分布的方均根偏差(RMSD),體現了分布廣度或者說彌散程度。比如σ對于空穴的x分量定義為
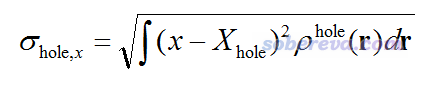
σ的模,即三個分量平方和開根號,筆者稱之為σ指數,衡量的是空穴或電子的整體分布廣度。
然后可以定義以下量
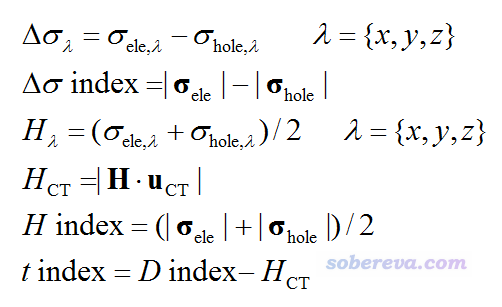
下面依次介紹下這些量的用途
Δσ_λ:衡量在λ方向上電子與空穴的空間分布廣度之差。
Δσ指數:體現的是電子與空穴的總體空間分布廣度之差。
H_λ:衡量在λ方向上空穴和電子的平均延展程度。
H_CT:衡量在CT方向上空穴和電子的平均延展程度。式中的粗體H就是H_x、H_y、H_z合在一起寫成的矢量,粗體u_CT是CT方向上的單位矢量,利用電子和空穴的質心位置可直接得到。
H指數:體現的是電子與空穴的總體平均分布廣度
t指數:衡量空穴和電子的分離程度。t指數>0就暗示由于CT使得空穴和電子分離較為充分,因為空穴和電子的質心距離較遠,同時它們在此方向上的平均延展程度相對來說又不是那么高。t指數<0就可以認為在CT方向上空穴和電子沒有顯著分離,因為此時空穴和電子的質心距離相對于它們的平均延展程度來說沒有那么大。
在《圖解電子激發的分類》(http://sobereva.com/284)中介紹了怎么判斷電子激發類型,常見的就是LE(局域激發)、CT(電荷轉移激發),另外還有里德堡激發等。根據筆者的研究經驗,利用上述指數,對電子激發類型一般可按照如下方式進行區分。
·局域激發(或整體激發):D指數小,Sr較大,t指數明顯為負,Δσ指數不大。這種激發的空穴和電子主要分布范圍很接近,重疊程度顯然也低不了,空穴和電子分布沒有明顯分離,而且分布廣度相仿佛
·單方向電荷轉移激發:D指數大,其它指標大小不一定。既然是CT激發顯然電子和空穴的距離必須大,而空穴和電子的重疊程度則可大可小,重疊大的時候說明電子和空穴分離尚不充分,而重疊小的時候說明電子和空穴分布已經高度分離了
·中心對稱的電荷轉移激發:有的體系電子激發時電荷轉移可以往多個方向進行,中心對稱的電荷轉移激發是理想化的情況,應具有的特點是D指數小,Δσ指數很大
·里德堡激發:D和Sr指數都不大,Δσ指數很大。這種激發的空穴和質心距離相差一般不顯著,但是電子分布范圍遠比空穴分布范圍彌散,因此重疊度不會太高
以上判斷方式對一般情況都是適用的,但也不排除遇到極個別反例的情況。可以在寫論文的時候把一堆激發態的各種指數以列表方式給出來,但至少也應當同時考察一下空穴和電子分布圖,這樣在討論時心里明顯更有數、更放心,而不會被數字蒙在鼓里。
另外,別去苛求定義個諸如“D大于xxx就證明是電荷轉移激發”這種判斷標準,一刀切是使不得的。應該算作哪種激發,應當將各種指數還有空穴、電子分布圖結合起來分析判斷。另外,有的電子激發本身就是諸如CT和LE激發高度混合的模式,非要搞個嚴格標準來劃分成要么CT要么LE一點意思也沒有,也很有誤導性。
筆者還定義了空穴離域指數(hole delocalization index, HDI)和電子離域指數(electron delocalization index, EDI),如下所示。HDI(EDI)數值越小,說明空穴(電子)離域程度越高,即分布的均勻程度越大、攤得越開。這兩個量在定義上與筆者定義的軌道離域指數有類似之處,見《通過軌道離域指數(ODI)衡量軌道的空間離域程度》(http://www.shanxitv.org/525)。
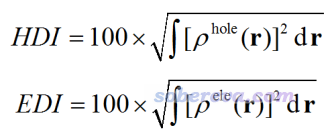
注:雖然|σ_hole|(|σ_ele|)越大往往也能暗示空穴(電子)的分布均勻程度越大,但對于空穴(電子)集中分布在多個區域的時候,就不能體現這點了,因為此指數假定空穴(電子)的主體分布能被單一高斯函數近似描述。而HDI、EDI則是普適的。
2.5 空穴、電子分布的平滑化描述
計算出前面提到空穴和電子的σ、質心位置后,根據J. Chem. Theory Comput., 7, 2498 (2011)的思路,筆者定義了可以把空穴和電子分布平滑化描述的Chole和Cele:
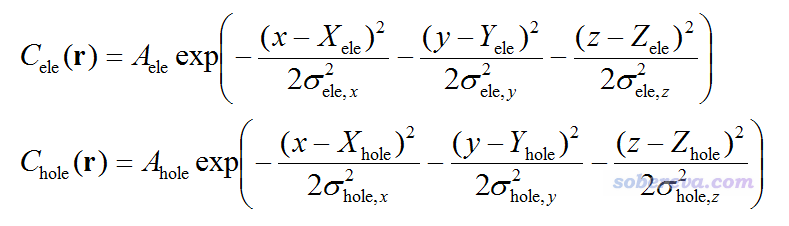
上式中A是歸一化系數,使得Cele和Chole全空間積分都為1。x,y,z是坐標矢量r的三個笛卡爾分量。如果你觀看Cele或Chole等值面圖,它們的正中心位置就恰好是質心位置。
定義Chole和Cele的意義在于,空穴和電子的分布往往比較復雜,等值面圖節面多,往往空穴和電子分布還相互交替,給圖形化考察帶來不便。而Chole和Cele等于把空穴和電子的分布等效地用高斯函數描述,抹去了分布細節,此時空穴和電子的等值面圖變成了橢圓形狀,在圖形化考察時明顯更為清楚、直觀。如果Chole或Cele等值面看起來比較接近圓形,說明空穴或電子在各個方向分布的延展程度比較相近;如果等值面看起來是明顯的橢圓,就說明在長軸方向上延展程度比其它方向上高得多;如果等值面圖是個扁圓,則說明在最短軸方向上延展程度都比其它方向上低得多。
2.6 空穴-電子間的庫侖吸引能(激子結合能)
電子是帶負電的,而電子離開的地方,即空穴,相應地帶正電,因此電子和空穴之間有庫侖吸引能,也被叫做激子結合能(exciton binding energy),可根據簡單庫侖公式計算,如下所示
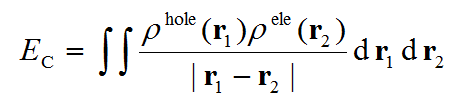
有不少文章通過上式計算并討論了激子結合能,比如J. Chem. Phys., 143, 244905 (2015)、J. Phys. Chem. C, 121, 17088 (2017),但是他們是把本征值最大的占據和非占據NTO對應的密度作為上式中空穴和電子,顯然沒有Multiwfn里這種空穴和電子定義那么理想,因為很多情況下貢獻最大的一對NTO躍遷對電子激發產生的貢獻往往遠到不了100%,偏差大到根本不可忽略,此時這樣算的激子結合能也不準。
Multiwfn根據上式計算激子結合能的時候目前用的是基于均勻分布的格點方式算的,哪怕格點數不是特別多的時候耗時也還是很高的,建議用性能較好的服務器計算。而且耗時和格點數的二次方呈正比,而和格點間距六次方成反比。格點間距太大,則格點質量比較糙,雖然耗時低,但計算精度差;格點間距太小,精度好,但耗時會很高。因此格點間距應恰當選取,適當時候可以做計算結果隨格點間距的收斂性測試,看什么時候結果基本不隨格點數增加有明顯變化,那么此時的格點數就夠用了。
另外,激子結合能還有一種定義,就是垂直電離能(VIP)減去垂直電子親和能(VEA)再減去optical gap(最低電子激發能)。這種定義和上面那種定義在理論上和實際數值上相差較大,沒有顯著聯系。
2.7 Ghost-hunter指數
Ghost-hunter指數本身不屬于空穴-電子分析范疇,但由于利用到前述的D指數,而且Multiwfn也會在空穴-電子分析過程中輸出這個指數,所以這里順帶提一下。
純泛函和低HF成份的雜化泛函對大共軛體系很可能出現ghost激發態,這是由于泛函的自相互作用誤差(SIE)問題導致的虛假的電荷轉移激發態。這些激發態的激發能很低,振子強度接近0,其存在會浪費計算量,還會妨礙正確判斷、討論感興趣的激發態(比如初學者可能會把ghost態誤當成了S1態去討論熒光發射特征)。一般為了避免ghost態出現,可以用高HF成份泛函如M06-2X,或者長程校正泛函如wB97XD,或者長程區域HF成份很高的泛函如CAM-B3LYP來避免。為了判斷當前TDDFT計算是否可能存在ghost態,J. Comput. Chem., 38, 2151 (2017)一文提出了ghost-hunter指數。筆者認為原文的定義不是特別理想和嚴格,而且存在錯誤,在Multiwfn的空穴-電子分析模塊中計算ghost-hunter指數時用的是筆者自己在原始定義基礎上稍作修改的定義:
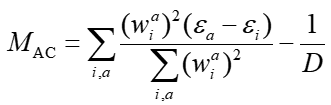
此式中,ε是分子軌道能量,i和a對應占據和非占據軌道,D就是前面提到過的空穴和電子質心之間的距離。ghost-hunter指數用M_AC符號表示,其對應的全稱是Mulliken averaged configuration。JCC文章認為,ghost-hunter指數是電荷轉移激發的激發能的理論下限,如果TDDFT算出來的某個態的激發能低于相應的ghost-hunter指數,這個態就算ghost態,反之就不算ghost態。這種判斷方式有物理意義和合理性,但是根據筆者的實際測試發現,這種判斷ghost態的標準往往太過激了。有時算出的激發能低于ghost-hunter指數一些,但憑基本理論知識可以判斷出實際上這并不是ghost態。所以ghost-hunter指數僅供參考,頂多也就是當做判斷ghost態的一個必要而非充分條件,千萬別太盲目用它說事!如果你用的是諸如CAM-B3LYP或wB97XD這種長程區域HF成份較高或100%的泛函,其實根本不需要擔心出現ghost態的問題,就算ghost-hunter指數判斷成是ghost態也不要太當回事(尤其是激發能不是很低,且振子強度也不是特別接近0的情況,本來就不可能是ghost態)。
注意,JCC原文里計算ghost-hunter指數是基于昂貴的弛豫的激發態密度與基態密度差所計算出的D指數算的ghost-hunter指數,但在Multiwfn的空穴-電子分析模塊里則是基于空穴和電子分布得到的D算的ghost-hunter指數,因此和原文的做法是存在定量差異的。Multiwfn中的這種實現是絕對合理的,可以放心使用。如果就是想基于弛豫的激發態密度與基態密度差對應的D來計算ghost-hunter指數,應該利用Multiwfn的基于密度差的電荷轉移分析功能自行計算D,詳見手冊3.21.3節的介紹和4.18.3節的例子。另外注意,ghost-hunter指數只適合判斷單方向的CT激發,不能用于判斷多方向CT激發是否有ghost態的可能。
3 空穴-電子分析在Multiwfn中的使用簡介
3.1 輸入文件
Multiwfn主功能18中的子功能1用于實現空穴-電子分析(還能實現躍遷密度、躍遷偶極矩密度分析,本文暫不討論)。此分析需要以下兩類文件,更具體說明參見Multiwfn手冊3.21節開頭。
1 記錄了參考態波函數的文件,是剛啟動Multiwfn時就需要載入的
2 記錄了激發態組態系數的文件,是進入空穴-電子分析功能時需要載入的
簡單來說,對于Gaussian用戶,要做空穴-電子分析一般就用TDDFT算激發態即可(不常用的CIS、TDHF、TDA-DFT也支持),閉殼層和開殼層參考態都支持,對單個結構做TDDFT以及對激發態用TDDFT做優化都可以(對于后者,分析的是最后一步結構的情況)。計算時候必須帶IOp(9/40=4)關鍵詞使得絕對值大于1E-4的組態系數都輸出出來。把算完得到的chk轉換為fch文件后就可以作為第1類文件,而Gaussian輸出文件可作為第2類文件使用。
Multiwfn做空穴-電子分析最主要的一環就是計算空穴和電子的格點數據,從而能夠可視化它們的分布,以及計算D、Sr/Sm、H、t等指數。對于較大體系,基于IOp(9/40=4)的輸出文件計算空穴和電子的格點數據耗時往往還是挺高的,為了節約時間,可以改為使用IOp(9/40=3)關鍵詞,這樣輸出的組態系數會少一些,顯然空穴-電子分析的耗時就會降低不少,但代價是計算精度會有所損失,不過好在損失程度一般來說小到可以忽略。默認情況下Gaussian用的是IOp(9/40=1),此時空穴-電子分析誤差就太大而根本無法接受了。
Multiwfn支持的一大堆電子激發分析,也包括此文介紹的空穴-電子分析,絕不僅限于Gaussian用戶能用,諸如GAMESS-US、Firefly、ORCA等用戶也可以用,詳見手冊3.21節開頭的說明。很值得一提的是ORCA支持的sTDA和sTDDFT的任務的輸出文件結合molden文件也可以用于當前分析。sTDA和sTDDFT分別是對TDA-DFT和TDDFT的高度簡化,只要基態DFT軌道算出來了,則激發態就可以用這兩種方法以近乎為0的耗時計算出來,因此Multiwfn的空穴-電子分析甚至可以用于超過500個原子的情況(因為DFT單點是可以算得動的)。
3.2 基本操作
進入空穴-電子分析功能后,會列出程序識別出的所有激發態的簡要信息,并讓你選擇要考察的激發態。如果分析過之后還要分析其它態的話,先退出空穴-電子分析,然后再重新進入此功能并且選擇其它激發態即可。在空穴-電子分析主界面里,有這些選項:
(1)計算空穴、電子、CDD、Sr、Sm、Chole、Cele以及躍遷密度、躍遷偶極矩等函數的格點數據。選這個選項后,先要對格點進行設定,相當于把體系套入一個矩形盒子里,盒子邊緣與體系邊緣原子有一定距離,要計算的格點均勻分布在這個盒子里。有了格點數據,才能進而可視化各種函數、通過格點積分方法計算各種指數。一般來說,小體系建議選中等質量格點(對應約512000個點),好幾十原子的中等體系建議選高質量格點(對應約1728000個點);若是上百原子的大體系,1728000個點的情況下格點間距都可能偏大導致圖像粗糙、各種指數計算不很準確,此時建議通過直接輸入格點間距的模式設定恰當的格點間距(一般0.25~0.3 Bohr可以達到精度和耗時的權衡)。格點數據計算完了之后,前面提及的各種基于空穴和電子分布定義的定量指標以及其它一些指標如ghost-hunter指數都會輸出出來。之后會看到后處理菜單,在里面可以觀看各種函數的等值面圖,也可以將它們導出成.cub文件便于之后在VMD等第三方程序里作圖獲得更好圖像效果。后處理菜單還有相應的選項用于計算空穴和電子之間的庫侖吸引能。
(2)輸出分子軌道對空穴和電子的貢獻。由于分子軌道數目太多,全輸出的話太占屏幕,因此程序會讓你輸入個閾值,只有對空穴或電子貢獻大于這個閾值的軌道才會被顯示出來。
(3)輸出原子或片段對空穴和電子的貢獻并且繪制成填色圖。進入此功能后,先選擇計算原子對空穴、電子貢獻的方法,然后屏幕上馬上輸出各個原子對空穴、電子以及Sr指數的貢獻百分比。之后會出現個菜單,用相應選項可以把貢獻值導出到文本文件里、把原子對空穴/電子/Sr指數的貢獻繪制成熱圖(heat map,即填色矩陣圖)、調節作圖選項。若選擇-1就可以定義片段,片段可以直接輸入,也可以從你指定的文本文件中讀取(此文件里每個片段定義占一行,內容比如1,5-10,12,19,可以有無數個片段),之后屏幕上馬上就會輸出各個片段對空穴、電子以及Sr指數的貢獻百分比。然后再用相應選項繪制熱圖的時候,橫坐標就不再是原子序號了,而是片段序號。
計算原子對空穴、電子貢獻的方法可以選擇Mulliken和Hirshfeld兩種(見下文)。Mulliken方式計算的耗時極低,但是計算激發態時候用的基組絕對不能帶彌散函數,否則結果將毫無意義。另外,由于Mulliken劃分形式的理論缺陷,有的原子對空穴或電子的貢獻有可能為負值,這種情況就把貢獻視為0就完了,這樣的原子的Sr指數會被Multiwfn自動當成0。但如果負值很明顯,比如超過-3%,那么當前的結果就很不可靠了。如果由于特殊原因不得不用彌散函數(比如計算陰離子體系的激發態或者里德堡激發),或者用Mulliken方式計算原子對空穴和電子的貢獻時出現特別顯著的負值,那么建議選擇Hirshfeld方式計算,這明顯更昂貴,但是更可靠,非常普適。
順帶一提,Multiwfn還能基于Becke或Hirshfeld-I等方式計算原子或片段對空穴/電子的貢獻,但需要手動操作,由于步驟略多且比起Hirshfeld劃分沒明顯額外好處,故一般沒必要用:先用空穴-電子分析模塊的選項1計算空穴和電子的格點數據,然后把格點數據導出為cub文件。然后把settings.ini里的iuserfunc設為-1(此時用戶自定義函數將對應于基于格點數據插值產生的函數),啟動Multiwfn并載入電子或空穴的cub文件,進入主功能15(模糊空間分析),先利用選項-1選擇要用的劃分方式,然后選選項1(在各個原子模糊空間內積分特定函數),被積函數選擇用戶自定義函數,之后各個原子的貢獻值就輸出了。如果要計算某個片段貢獻的話,在模糊空間分析模塊中選擇選項1之前先選選項-5來定義片段即可,之后子功能1計算出來的所有原子加和值就對應了你定義的片段的貢獻量。
(4)輸出基函數對空穴和電子的貢獻。輸入一個閾值后,對空穴或電子貢獻超過這個閾值的基函數就會被輸出。這對于考察哪些原子軌道顯著參與了空穴和電子非常有用。只要搞清楚基函數與原子軌道間的對應關系,就可以通過把基函數對空穴/電子貢獻數值加和得到原子軌道對空穴/電子的貢獻。如果不知道對應關系怎么判斷,參看《利用布居分析判斷基函數與原子軌道的對應關系》(http://sobereva.com/418)。
Multiwfn里有很多選項,幾乎都是光看屏幕上的提示就知道怎么用、是什么含義、該輸入什么,這里就不具體說了,請睜大眼睛看清楚屏幕上的各種提示、仔細理解提示的含義,若還有不懂的請仔細閱讀本文、手冊相關章節并且自行嘗試。
4 空穴-電子分析實例
下面將通過三個具有代表性的體系演示Multiwfn的空穴-電子模塊的使用,一個是D-pi-A體系,一個是配合物體系,一個是里德堡激發的研究。如果對Gaussian的TDDFT計算不熟悉,務必參看《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》(http://sobereva.com/314)。本文例子的輸入輸出文件皆可在此下載:http://sobereva.com/attach/434/file.rar。本文使用的是Gaussian16 A.03版。
4.1 D-pi-A體系:NH2-biphenyl-NO2
首先我們對NH2-biphenyl-NO2體系的幾個激發態用空穴-電子分析框架里的方法進行電子激發特征的討論。此體系結構如下,NH2是電子給體(Donor)基團,聯苯起到pi橋作用,NO2是電子受體(Acceptor)基團。
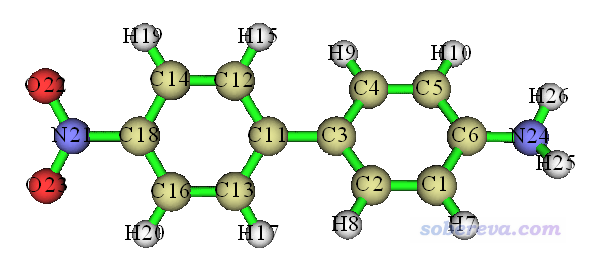
首先對此體系在常用的B3LYP/6-31G*級別下進行優化,然后用以下設定做TDDFT計算,將得到5個單重態激發態。IOp(9/40=4)如前所述必須要加上。
%chk=D-pi-A.chk
# CAM-B3LYP/6-31g(d) TD(nstates=5) IOp(9/40=4)
計算完畢后將D-pi-A.chk轉換為D-pi-A.fch,不會轉換的話看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://sobereva.com/379)。用CAM-B3LYP是因為此泛函做TDDFT描述電荷轉移激發比較不錯,當前體系有一些激發態是電荷轉移激發態。普通有機體系用6-31G*做TDDFT就足矣得到合理的結果。
啟動Multiwfn,依次輸入
D-pi-A.fchk //首先載入含有參考態波函數信息的文件
18 //電子激發分析
1 //空穴-電子分析
D-pi-A.out //Gaussian輸出文件,里面含有空穴-電子分析需要的組態系數信息
1 //首先我們分析基態(S0)到第1激發態(S1)的電子激發特征
1 //考察空穴、電子等函數的圖形及各種指數
2 //當前體系不大,用中等質量格點就夠了
此時屏幕上輸出了大量信息,如下所示。凡是涉及到積分得到的指數,比如D、Sr等,都是通過均勻格點積分得到的,顯然格點質量越高(間距越小),數值誤差會越小。
Integral of hole: 1.000343
Integral of electron: 0.999793
Integral of transition density: -0.000033
Transition dipole moment in X/Y/Z: 0.444063 -0.000186 -0.001753 a.u.
Sm index (integral of Sm function): 0.27369 a.u.
Sr index (integral of Sr function): 0.51896 a.u.
Centroid of hole in X/Y/Z: -4.531729 0.000425 0.003252 Angstrom
Centroid of electron in X/Y/Z: -4.010033 0.001760 0.002643 Angstrom
D_x: 0.522 D_y: 0.001 D_z: 0.001 D index: 0.522 Angstrom
Variation of dipole moment with respect to ground state:
X: -0.985930 Y: -0.002523 Z: 0.001150 Norm: 0.985934 a.u.
RMSD of hole in X/Y/Z: 1.443 1.160 0.437 Norm: 1.902 Angstrom
RMSD of electron in X/Y/Z: 1.596 0.974 0.634 Norm: 1.974 Angstrom
Difference between RMSD of hole and electron (delta sigma):
X: 0.153 Y: -0.186 Z: 0.197 Overall: 0.072 Angstrom
H_x: 1.520 H_y: 1.067 H_z: 0.536 H_CT: 1.520 H index: 1.938 Angstrom
t index: -0.998 Angstrom
Hole delocalization index (HDI): 22.68
Electron delocalization index (EDI): 17.11
Ghost-hunter index: -18.831 eV, 1st term: 8.771 eV, 2nd term: 27.601 eV
Excitation energy of this state: 3.907 eV
Integral of hole和Integral of electron分別是空穴和電子在全空間的積分值,理論上應該恰好是1.0,但由于數值積分終究有誤差,所以我們算出來的稍微偏離1.0,但由于偏離極小,因此對于當前體系當前的激發態來說,我們用的格點設定是合適的。如果發現偏離1.0非常大,那么得到的各種指數也都會不可靠,可能性有三:(1)忘了用IOp(9/40=3或4) (2)格點質量太低 (3)盒子的延展距離不夠大,導致在空穴/電子有明顯分布的區域沒有被格點覆蓋(尤其是考察里德堡激發時,默認的延展距離肯定不夠大)。對后兩種情況,在格點設定的界面里用相應選項進行調整即可。
上面輸出的其余部分依次是:躍遷密度在全空間的積分(理想值為0)、躍遷電偶極矩、Sm和Sr指數、空穴和電子的質心坐標、Dλ和D指數、激發態偶極矩相對于基態偶極矩的變化的X/Y/Z分量和模、空穴和電子的RMSD、空穴和電子的RMSD在X/Y/Z方向的差值(Δσ_λ)以及Δσ指數、H_λ和H_CT和H指數、t指數、空穴和電子離域指數、Ghost-hunter指數、激發能。Ghost-hunter index后面的1st term和2nd term后面的兩個值分別是Ghost-hunter指數表達式中的第一項(依賴組態系數和軌道能量的部分)和第二項(1/D),二者之差就是Ghost-hunter index。最后給出的激發能是從Gaussian輸出文件里直接讀的。
上面輸出的躍遷偶極矩是利用均勻格點積分得到的,從Gaussian輸出文件里也可以直接讀到,X/Y/Z三個分量為0.4427、-0.0005、-0.0012 a.u.,這和Multiwfn輸出的0.444063、-0.000186、-0.001753 a.u.極為相近,這也進一步表明當前的積分格點設置是合理的。
當前S0->S1這個激發,從上面的輸出中看到D指數才0.522埃,還不到半個C-C鍵的長度,明顯算是個很小的值。而Sr指數達到0.519(上限值為1.0),相當于空穴和電子有一半多一點的分布特征都已經完美重合上,故已經算很大了。所以,光從Sr和D,我們就已經能判斷這應該是一個LE激發。我們再看t指數,總值為-0.998,明顯小于0,這意味著空穴和電子的分布沒有顯著的分離,同樣也暗示了這應該是個LE激發。
現在屏幕上會看到后處理菜單,每個選項的含義都不言自明,請讀者仔細瀏覽一遍每個選項。這里我們選擇3,會同時看到空穴和電子的分布,如下圖的上半部分所示。然后關閉圖形窗口,選擇8來同時觀看Chole和Cele,如下圖的下半部分所示,為了看著清楚用了透明風格(圖形窗口上方有菜單可以設置顯示風格)。圖中綠色代表電子分布,藍色代表空穴分布。繪制的時候等值面數值(isovalue)都是設的0.005,設多大合適沒有確切標準,應該反復調節,看什么時候對應的等值面圖最能把當前電子激發的主體特征充分展現出來并且便于我們討論(提醒:對于Chole和Cele分布得極其廣闊的情況,它們的等值面在默認的isovalue下是看不到的,必須自己逐漸一點點減小isovalue直到能看得到為止)。
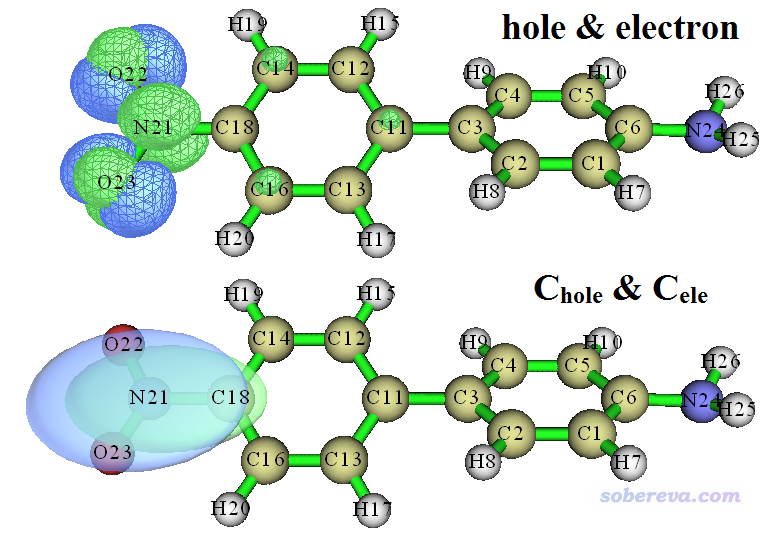
由上圖可見,空穴和電子幾乎只出現在硝基部分,因此毫無疑問S0->S1是局域激發,驗證了我們基于D、Sr、t指數所下的結論。Chole和Cele的圖形看上去顯然更直觀一些,非常圓滑,沒有空穴和電子分布圖那么多節面。另外,根據上面的空穴圖,空穴看起來是由氧的孤對電子軌道構成的,因為在每個氧兩側各有一個瓣,而且沒用于成鍵;而從電子圖上看,電子在NO2的平面上有個節面,因此電子分布應當是由pi*軌道構成的,故我們可以將S0->S1指認為n->pi*特征的局域激發。
我們接下來看一下空穴和電子的重疊函數。在當前的圖形窗口上點Return,在后處理菜單選選項4,然后選2,就顯示出了Sr函數圖,如下圖上半部分所示。關閉窗口,選擇7,就顯示出了激發態與基態間的密度差(CDD)圖,如下圖下半部分所示,綠色和藍色分別對應激發態密度相對于基態密度增加和減少的部分。繪制這兩個圖的時候用的等值面數值都是0.005。
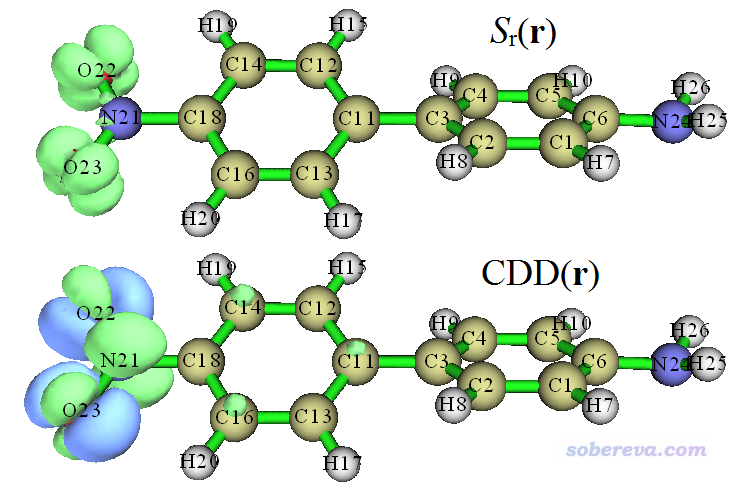
從Sr圖上,可以清楚看出空穴和電子在哪些地方有顯著交疊。如上圖所示,每個氧周圍有四個空穴與電子高度交疊的區域,對照之前的空穴和電子等值面圖就很容易明白Sr圖形為什么是這樣。上面的CDD圖和之前展示的把空穴與電子同時顯示在一起的圖(簡稱為“空穴&電子圖”)比較像,但是也存在差異,關鍵差異就在于CDD把電子和空穴求差,展現的是二者在交疊區域已經發生過抵消的圖;而空穴&電子圖當中則是可以看到空穴與電子之間的相互交疊特征的。我認為空穴&電子圖比CDD明顯更適合考察電子激發的內在特點,因為它直接展現出了未經抵消過的空穴和電子的原始分布特征。
我們若在后處理菜單中選擇18,程序就會開始計算空穴-電子之間的庫侖吸引能,計算較為耗時,輸出為:
Coulomb attractive energy: 0.287031 a.u. ( 7.810524 eV )
接下來,再演示一下計算軌道對空穴和電子的貢獻。在后處理菜單選擇0,就退回到了電子-空穴分析界面,然后選擇2,再輸入一個輸出閾值,這里輸入1,代表把對空穴或者電子貢獻超過1%的軌道輸出。此時屏幕上馬上看到以下內容:
MO 52, Occ: 2.00000 Hole: 96.207 % Electron: 0.000 %
MO 56, Occ: 2.00000 Hole: 3.415 % Electron: 0.000 %
MO 57, Occ: 0.00000 Hole: 0.000 % Electron: 85.411 %
MO 59, Occ: 0.00000 Hole: 0.000 % Electron: 12.222 %
MO 61, Occ: 0.00000 Hole: 0.000 % Electron: 2.163 %
Sum of hole: 100.001 % Sum of electron: 100.001 %
由數據可見,MO52對空穴產生絕對主導,貢獻達到96.2%,而電子則主要由MO57構成,貢獻達到85.4%。這說明,如果你只通過MO52和MO57這兩個軌道來說事,雖然能對這個電子激發予以定性的描述,但還是有不可忽略的偏差。上面Sum of hole和Sum of electron分別是所有軌道對空穴和電子的貢獻的總和(包括屏幕上沒有輸出的項),顯然理應為精確的100%,但可見當前輸出值有個0.001%的誤差,完全可以忽略,這誤差來自于Gaussian輸出文件里并沒有輸出所有的組態,我們通過IOp(9/40=4)只要求了組態系數絕對值大于0.0001的才被輸出。
我們再看看原子和片段對空穴和電子的貢獻。在電子-空穴分析界面里選擇3,然后選擇1用Mulliken劃分方式,之后馬上看到以下輸出:
The number of non-hydrogen atoms: 16
Contribution of each non-hydrogen atom to hole and electron:
1(C ) Hole: 0.19 % Electron: 0.02 % Overlap: 0.07 % Diff.: -0.17 %
2(C ) Hole: 0.18 % Electron: 0.48 % Overlap: 0.30 % Diff.: 0.30 %
3(C ) Hole: 0.59 % Electron: 0.13 % Overlap: 0.28 % Diff.: -0.46 %
4(C ) Hole: 0.18 % Electron: 0.49 % Overlap: 0.30 % Diff.: 0.32 %
5(C ) Hole: 0.19 % Electron: 0.02 % Overlap: 0.06 % Diff.: -0.18 %
6(C ) Hole: 0.31 % Electron: 0.37 % Overlap: 0.34 % Diff.: 0.06 %
11(C ) Hole: 0.15 % Electron: 4.17 % Overlap: 0.78 % Diff.: 4.03 %
12(C ) Hole: 0.41 % Electron: 0.14 % Overlap: 0.24 % Diff.: -0.26 %
13(C ) Hole: 0.37 % Electron: 0.14 % Overlap: 0.23 % Diff.: -0.23 %
14(C ) Hole: 0.94 % Electron: 5.03 % Overlap: 2.18 % Diff.: 4.09 %
16(C ) Hole: 0.92 % Electron: 5.01 % Overlap: 2.15 % Diff.: 4.09 %
18(C ) Hole: -0.01 % Electron: 1.16 % Overlap: 0.00 % Diff.: 1.17 %
21(N ) Hole: 2.39 % Electron: 33.90 % Overlap: 9.00 % Diff.: 31.52 %
22(O ) Hole: 46.18 % Electron: 24.38 % Overlap: 33.55 % Diff.: -21.80 %
23(O ) Hole: 46.12 % Electron: 24.39 % Overlap: 33.54 % Diff.: -21.73 %
24(N ) Hole: 0.46 % Electron: 0.15 % Overlap: 0.26 % Diff.: -0.32 %
由于氫原子一般不怎么參與電子激發,所以上面只輸出了非氫原子的信息,包括原子對空穴、電子、空穴與電子的重疊、電子與空穴的差值(即CDD)的貢獻,公式在本文2.3節已經介紹了。硝基上的原子序號是21、22、23,由數據可見,硝基的氧對空穴起了主導貢獻,兩個氧加起來貢獻了92%。而電子分布的離域特征相對更強一些,硝基上的三個原子一共貢獻了大約83%,剩下的大多是聯苯上的原子貢獻的。雖然通過考察空穴、電子等值面圖就可以考察它們的分布特征,但是圖像明顯依賴于等值面選取,沒法僅通過一張圖就全面展現所有區域的空穴和電子分布特征。而如上給出的原子的定量貢獻值,則是較確切、嚴格的。21N、22O和23O的Diff.加和約為-12%,體現出在硝基區域密度差的積分值是負值,即硝基部分是失電子的,有一部分轉移到了聯苯上(如果想考察具體轉移量,建議用Multiwfn中的IFCT方法,見http://www.shanxitv.org/433)。
我們還可以把原子的貢獻值繪制成熱圖。在當前菜單里先選擇4然后輸入1,把橫坐標步長間隔改為1,然后選擇1 Plot hole/electron composition as heat map,就會馬上看到以下圖像

圖中橫坐標是非氫原子序號,從1開始連續排,此圖通過顏色描述了各個非氫原子對空穴、電子以及二者重疊的貢獻大小(諸如0.4就代表40%)。根據前面給出的非氫原子對空穴/電子的貢獻數值列表,我們可以知道諸如圖中橫坐標為16的位置對應的實際上是N24原子。為了令圖的橫坐標和原子位置對應起來更方便,大家可以把fch/gjf/out文件用gview打開,進入Edit - Atom List,選Edit - Reorder - All atoms: Hydrogens Last,此時gview顯示的就是以下圖像,所有氫原子的序號都被放到非氫原子后頭了,因此圖中非氫原子的序號就和Multiwfn繪制的原子對空穴/電子貢獻的熱圖的橫坐標直接對應了。
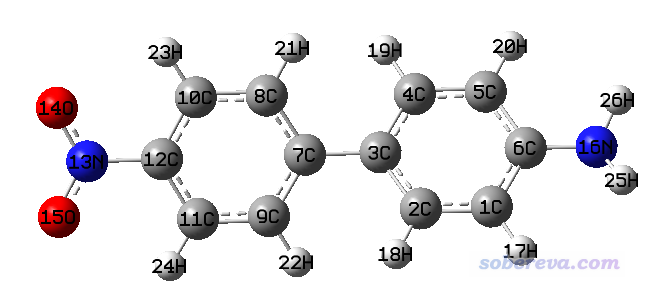
和gview顯示的序號一對照就知道,熱圖橫坐標的13、14、15的位置對應硝基的氮和兩個氧原子,16對應氨基的氮,其余的都是聯苯上的碳。熱圖的hole那一行非常直觀地體現出,空穴幾乎完全是硝基的氧貢獻的,因此相應矩陣元是紅色,對應很大數值。電子主要也是由硝基貢獻,但其它區域也有不可忽視的貢獻,因此熱圖的electron那一行在13~15以外一些區域呈現了藍色。熱圖的overlap那一行的顏色傳達的信息是電子和空穴在硝基氧上有顯著重疊(這和Sr函數等值面圖看到的現象一致),而在體系其它區域的重疊則遠沒有這么顯著。
在空穴/電子的成分分析界面里還有很多選項,可以調節熱圖的作圖效果、把圖像保存成圖片文件、切換是否把氫原子也納入熱圖,還可以把數據導出成he_atm.txt,以便之后自行在Origin等程序里繪制。這些選項就不一一說明了,請自行嘗試。其中有個選項-1很重要,通過它可以載入片段定義,從而輸出片段對空穴和電子的貢獻,之后還能繪制基于片段的熱圖,這使得討論明顯更為方便。此處我們把體系按照以下示意的方式劃分為四個片段
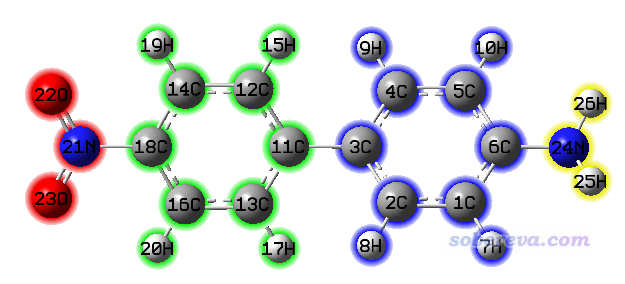
選擇選項-1,然后依次輸入
4 //定義四個片段(如果此處輸入0,將從指定的文本文件里讀取片段定義)
21-23 //片段1(硝基)的原子序號
11-20 //片段2(挨著硝基的苯)的原子序號
1-10 //片段3(挨著氨基的苯)的原子序號
24-26 //片段4(氨基)的原子序號
馬上看到了如下輸出
Contribution of each fragment to hole and electron:
# 1 Hole: 94.68 % Electron: 82.67 % Overlap: 88.47 % Diff.: -12.01 %
# 2 Hole: 3.20 % Electron: 15.67 % Overlap: 7.09 % Diff.: 12.47 %
# 3 Hole: 1.64 % Electron: 1.53 % Overlap: 1.59 % Diff.: -0.12 %
# 4 Hole: 0.47 % Electron: 0.13 % Overlap: 0.25 % Diff.: -0.34 %
基于片段給出的貢獻數據比基于原子給出的貢獻數據明顯清晰、易于討論得多。數據體現空穴有94.68%都在硝基上,而電子有82.67%在硝基上,其次有15.67%在挨著硝基的苯環上。在硝基上空穴與電子重疊有88.47%的程度。由于硝基上Diff.為-12.01%,當前考察的又是單電子激發,因此可以說硝基上的電子在電子激發過程中減少了0.1201個,這部分電子基本都跑到挨著硝基的苯環上了,由數據可見這個區域增加了0.1247個電子。然后,若想把上述數值展現得更直觀,我們可以選選項1繪制熱圖,此時的橫坐標已對應于片段編號了,如下所示:
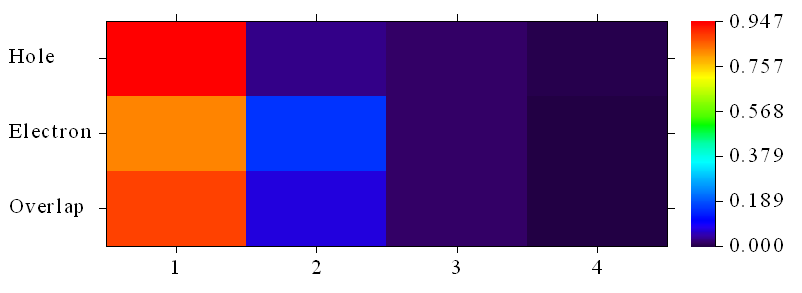
由圖明顯可見電子的分布廣度大于空穴的。
到此,對NH2-biphenyl-NO2這個體系的S0->S1激發的空穴-電子框架中的各種分析已經完整做了一遍。如果想再分析其它激發態,通過選項0退回到主功能18的菜單中,再次進入空穴-電子分析功能,然后選擇相應激發態即可。這里我們把這個體系所有算出來的5個激發態的D、Sr、H、t指數以及空穴-電子庫侖吸引能放在一起對照。之前還沒討論過的空穴離域指數(HDI)和電子離域指數(EDI)也一并給出了:
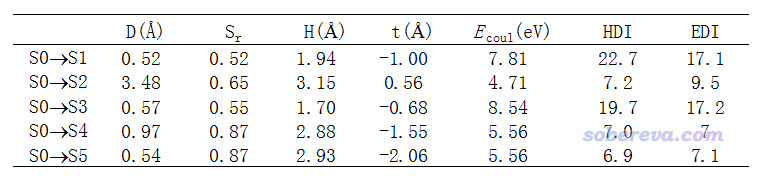
下面是所有這些激發的空穴&電子圖、Chole&Cele圖,以及Sr函數圖,繪制時候等值面數值用的都是0.003。可以看到Chole&Cele圖總是可以把空穴&電子圖蘊含的主體特征以更清晰直觀的方式展現出來,盡管丟失了很多細節,因此沒法判斷電子激發具體類型,比如是n->pi*還是pi-pi*等等。
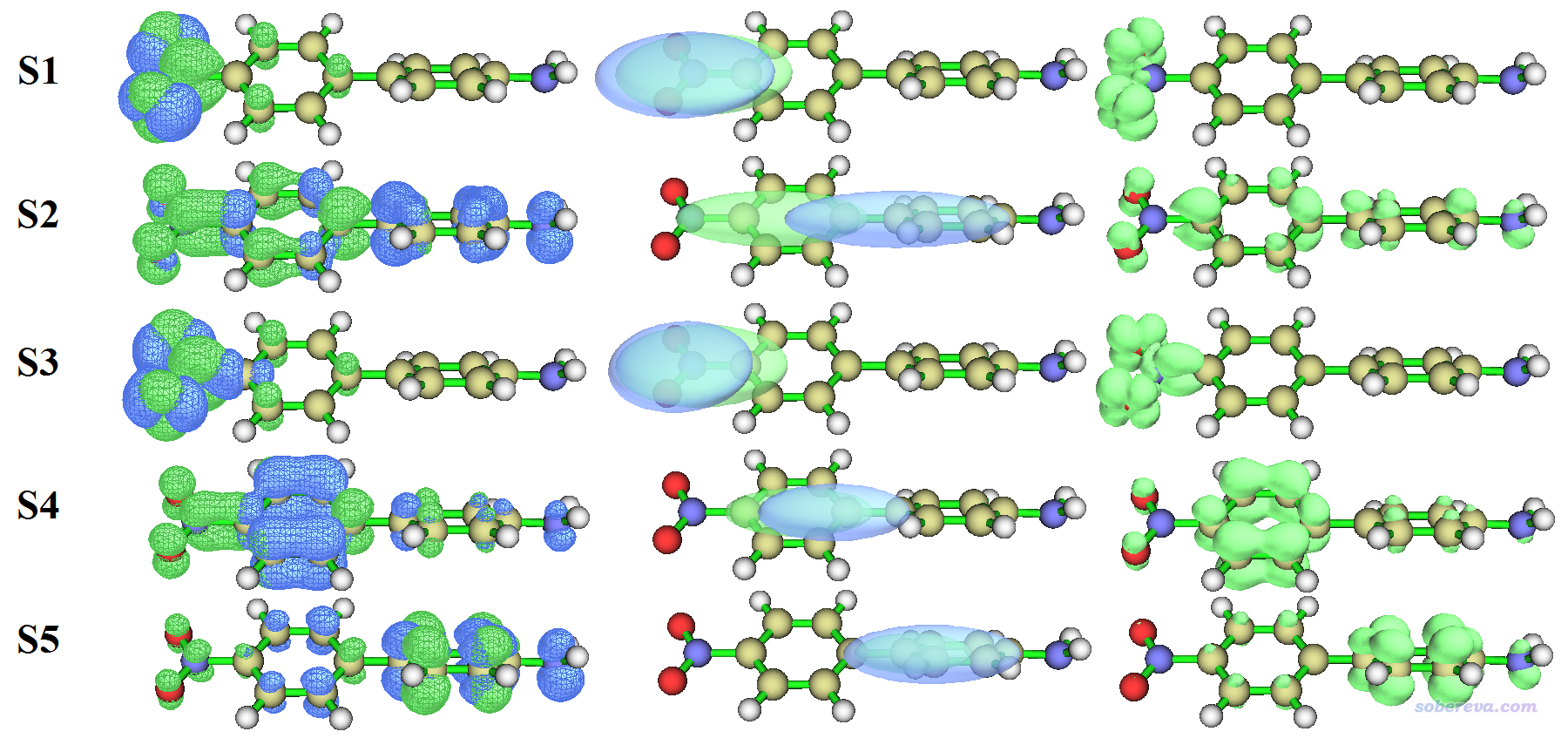
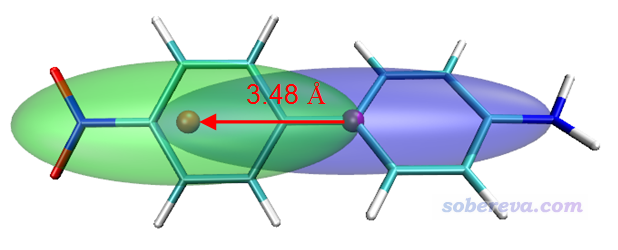
我們將指數和圖形結合來看,首先看電荷轉移距離。從D指數來看,只有S0->S2數值很大,高達3.48埃,明顯可以認為是電荷轉移激發,確實從Chole&Cele圖上也看到藍色和綠色等值面的中心(分別對應空穴和電子的質心位置)離得比較遠,而其它電子激發的藍色和綠色等值面中心相距都很近,明顯只能算是局域激發。
再看Sr指數,我們看到所有激發態的Sr指數都比較大,特別是S0->S4和S0->S5特別大,高達0.87,結合Sr函數圖和空穴&電子圖我們可以知道原因在于這兩種激發都是苯環上的高度局域的pi-pi*激發。雖然S0->S1也是高度局域的激發,但是它的Sr(0.52)甚至比S0->S2那種CT激發的Sr(0.65)還小,這是因為前面說過S0->S1體現的是n->pi*特征,由于孤對電子分布主體在NO2平面上,而pi*在NO2平面上是節面,因此S0->S1的Sr不算特別大,但也絕對算不上小。
再看H指數,反映了空穴和電子的平均分布廣度。從空穴&電子圖上可以看出,S0->S1和S0->S3激發的空穴和電子主體都分布在NO2那一小塊地方,因此H指數不大;而S0到S2、S4、S5的激發對應的空穴和電子的分布范圍都比較廣(在0.003等值面下,等值面甚至在整個體系各處都能看得到),因此H指數相對較大。從t指數上看,只有S0->S2的t指數為輕微的正值,表明空穴和電子分離較為明顯,因此更有理由把S0->S2認為是CT激發。而S0向其它激發態的激發對應的t都為顯著的負值,暗示電子與空穴分離度很低。
結合以上圖形和數據,我們可以對基態到5個激發態的特征進行確切的指認:
S0->S1:硝基上n-pi*局域激發
S0->S2:氨基到硝基方向上的pi-pi*電荷轉移激發
S0->S3:同S0->S1
S0->S4:發生在與硝基相連的苯環上的pi-pi*局域激發
S0->S5:發生在與氨基相連的苯環上的pi-pi*局域激發
上面給出的空穴-電子庫侖吸引能和電子激發特征有密切關聯,對其影響最大的是D。容易理解,D越大,空穴和電子主體分布越遠,因此空穴和電子的庫侖相互作用應當更弱。從數據看,確實S0->S2這個唯一的CT激發的空穴-電子庫侖吸引能的大小是所有5個電子激發中最小的,為4.71 eV。而S0->S1和S0->S3的激發,一方面D非常小,另一方面從H指數上看其空穴和電子分布的空間范圍又非常窄,可想而知憋在這一小塊地方的空穴和電子之間的庫侖吸引會非常強,從前面的表中來看確實如此,它們的空穴-電子庫侖吸引能是最大的(7.81和8.54 eV)。
將HDI、EDI分別與空穴、電子等值面進行對比,我們可以看到這兩個指數確實能很好地區分不同激發態的空穴和電子的空間離域程度的高低。比如對于S0->S1和S0->S3激發,從等值面圖上可見,它們的空穴和電子分布都是高度局域在硝基部分的,因此HDI和EDI都是相對較大的數值。而S0到其它三個激發態的躍遷的HDI和EDI都小得多,表明它們的空穴和電子都有明顯的離域特征,確實從等值面圖上也能看出這一點。因此HDI、EDI在定量化討論空穴和電子分布的離域程度方面很有價值、很靠譜。
這里也把所有5個激發態對應的片段對空穴、電子和二者重疊的貢獻的熱圖合在一起給出。是在Multiwfn輸出的五個激發態的圖像的基礎上稍微做了些拼接。圖中左上角示意了對片段的劃分。為了便于橫向對比,所有激發態的這個圖的色彩刻度統一設為了0.0~1.0。
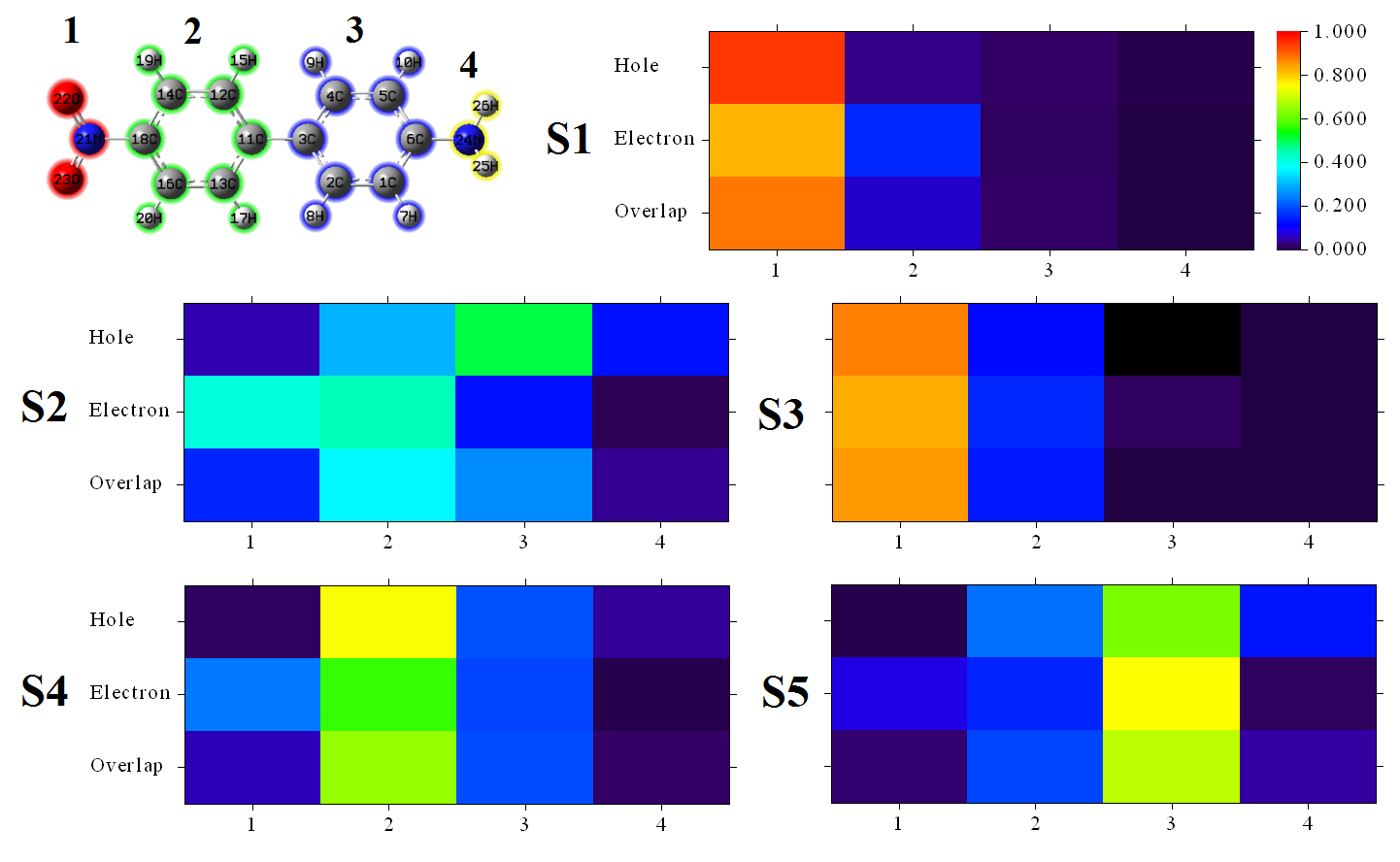
從這個圖上,看一下空穴和電子對應的行上的色彩鮮明的區域,就馬上知道電子是從哪轉移到哪的,比如從S0->S2的圖一看就知道被激發的電子主要來自片段3(靠近氨基的苯),大部分轉移到了片段1(硝基),少部分轉移到了片段2(靠近硝基的苯);其空穴和電子重疊區域比較分散,在片段2處重疊程度相對而言最高。再比如從S0->S4的圖上可看出被激發的電子是片段2的,激發后大部分還是留在片段2,但是也有一部分跑到了片段1,而空穴和電子的重疊在片段2上顯著高于其它部分。
這個NH2-biphenyl-NO2體系在《在Multiwfn中通過IFCT方法計算電子激發過程中任意片段間的電子轉移量》(http://sobereva.com/433)中也做了分析,文中將IFCT方法和空穴-電子分析相結合,在定量層面上透徹考察了電子激發過程中片段間電子轉移量,這是很有價值的信息,此文大家務必要看。
在空穴-電子分析的后處理菜單有很多選項可以把各種函數導出成cube文件,之后可以在免費的VMD程序(http://www.ks.uiuc.edu/Research/vmd/)里繪圖以獲得更好效果,筆者錄了一段視頻以演示具體操作,請大家觀看:《使用Multiwfn和VMD對配合物激發態繪制空穴-電子等值面圖》(https://www.bilibili.com/video/av28242597)。明顯更為理想的做法是利用筆者寫的VMD腳本來將空穴和電子繪制到一起,見《在VMD里將cube文件瞬間繪制成效果極佳的等值面圖的方法》(http://www.shanxitv.org/483),操作簡單至極,比手動在VMD里點擊各個選項來操作簡單得多,而且圖像效果極佳,如下所示(對應本例的S0-S4躍遷):
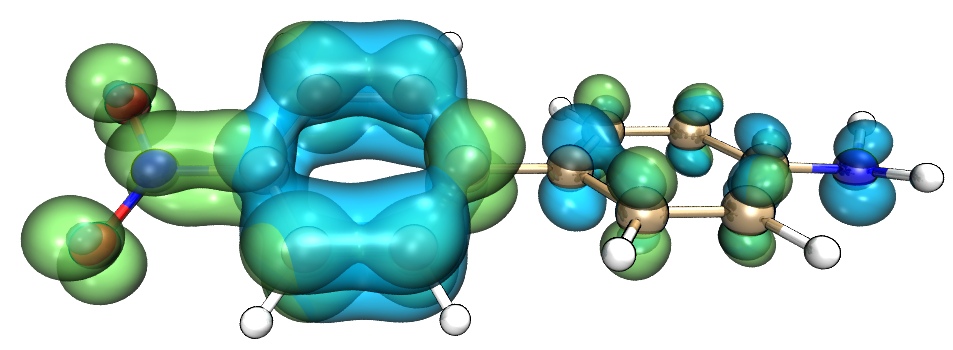
下圖是筆者在《一篇最全面、系統的研究新穎獨特的18碳環的理論文章》(http://www.shanxitv.org/524)對電子結構非常特殊的18碳環體系的S0->S1的激發用Multiwfn+VMD得到的空穴-電子等值面圖,可見非常漂亮,在此文中利用了這種分析對18碳環的電子激發特征做了透徹的分析,十分建議一讀!

另外,還可以在VMD里面利用繪圖命令在Chole&Cele的圖像上把質心位置標出來,使圖像上的信息更豐富。具體來說就是先在VMD里按如上方法把Chole&Cele的等值面圖繪制出來后,在VMD窗口中輸入類似以下命令
draw color purple
draw sphere {1.411500 -0.007015 -0.025494} radius 0.25 resolution 20
draw color orange
draw sphere {-2.069784 -0.000346 -0.000830} radius 0.25 resolution 20
這里draw color代表設定接下來繪制的物體的顏色,draw sphere用來在指定位置繪制半徑為radius的圓球。對于當前體系的S0->S2激發,對應的Chole&Cele的等值面如下,紫色和橙色圓球分別是空穴和電子的質心。為了更便于它人理解,還自行畫了個箭頭上去表示電子轉移方向,同時標注上了D指數。
4.2 配合物體系:Ru(bpy3)2+陽離子在水環境中
下面我們通過空穴-電子分析考察一下下面這個Ru(bpy3)2+陽離子配合物在水中的幾個激發態。
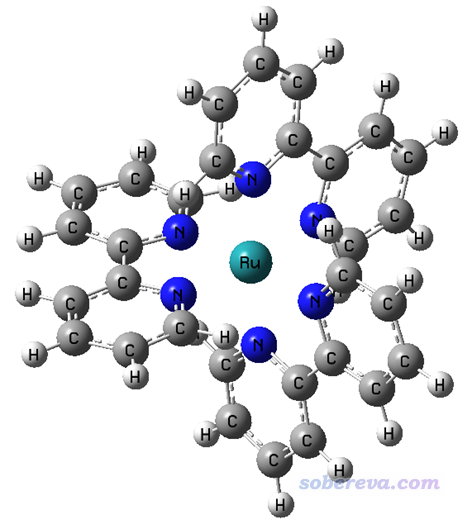
相應的Gaussian輸入文件在本文的文件包里,從中可見關鍵詞是
B3LYP/genecp TD(nstates=50) scrf IOp(9/40=3)
這里寫scrf就代表用Gaussian16默認的IEFPCM隱式溶劑描述水環境。由于此體系比較大,而且一次算50個激發態,為了避免計算空穴-電子分析耗時太高,以及避免輸出文件太大,這里用的是IOp(9/40=3),實際上此時的空穴-電子分析精度已經完全夠了。此例對配體用的6-311G*,對Ru用的SDD贗勢基組。
我們隨便選取幾個激發態使用Multiwfn做空穴-電子分析,結果如下

表中的D指數都非常小,而Sr指數都很大,這主要是因為當前體系是個對稱體系。表中的MLCT(%)是指metal-ligand charge transfer(金屬向配體電荷轉移)百分比。之前在《電子激發過程中片段間電荷轉移百分比的計算》(http://sobereva.com/398)里專門討論過怎么算,實際上利用空穴-電子分析的數據也可以算,而且很理想,就是將金屬在空穴中的百分比(即hole(Ru%))減去金屬在電子中的百分比(ele(Ru%))。注意,確切來說,這種方式得到的是凈MLCT量,里面已經和LMCT量(配體向金屬電荷轉移量)做了一定抵消。
下面是相應的空穴&電子圖,等值面數值都是0.002。由于S0->S24躍遷的空穴和電子分布區域有很大重疊,導致電子在金屬部分被空穴的等值面遮蓋,為了看得清楚,這里把空穴和電子的等值面單獨給出(在空穴-電子分析后處理菜單里有選項單獨顯示二者。單獨顯示空穴的時候等值面是綠色的,如果你把等值面數值改為負值,等值面就變成了藍色了)
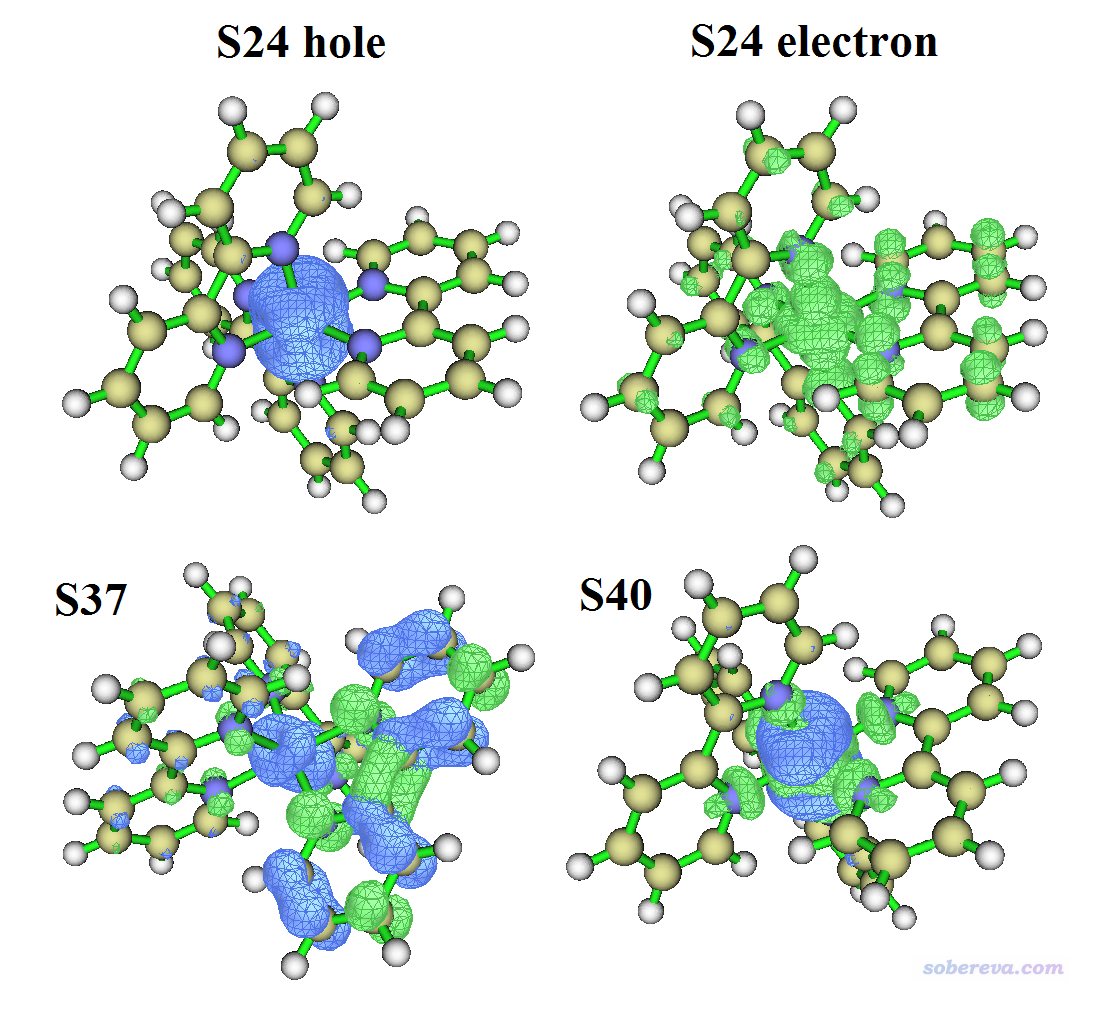
將圖形和定量數據結合可以很明顯看出,S0->S24激發既有metal-centered (MC)特征,即金屬上的電子激發到金屬自己的空軌道上,同時也有很高的MLCT成份。正如空穴&電子等值面圖所示,空穴的等值面主體是在金屬上,而電子的等值面則能看出有很大一部分跑到配體上去了。我們算出來的MLCT特征百分比為77.3-19.6=57.7%,應當說和空穴-電子等值面圖傳達的信息非常相符。注:空穴在配體上其實也有不可忽視的分布量,為100%-77.3%=22.7%,之所以空穴圖上沒看到,是因為空穴的分布在配體上攤得非常開,密度處處都不大,因此只有把等值面數值設得更小,比如0.0005,才能清楚看到空穴在配體上的分布。
再看S0->S37,從等值面圖可見空穴和電子的主體都在一個配體上,因此毫無疑問這是個LC (ligand-centered)激發,是這個配體的pi電子激發到它自己的pi*軌道上。由于空穴在金屬上也能看到一些分布,因此也有點MLCT特征,算出來是8.1%。
最后再看S0->S40,從空穴圖形和表格里的空穴在金屬上的百分比上看,空穴的分布特征和S0->S24別無二致,但電子在配體上的分布量明顯沒有S0->S24那么大,也就是有一定分布在和Ru直接配位的四個氮上,因此S0->S40的MLCT特征明顯弱于S0->S24,而相反,它的MC特征肯定比S0->S24的要大得多。
順帶一提,對這種配合物體系,你若想把MLCT、LMCT、LLCT、MC、LC特征具體數值全都分別得到的話應當用Multiwfn的IFCT分析,見《在Multiwfn中通過IFCT方法計算電子激發過程中任意片段間的電子轉移量》(http://sobereva.com/433)。
我們已經知道,S0激發到S24和S40的過程中電子主要來自Ru原子,但如何判斷被激發的是Ru的哪個原子軌道的電子?雖然從空穴的等值面圖上也多多少少能判斷出來,但還是有一些主觀性。為了弄清楚這點,我們可以計算基函數對空穴和電子的貢獻。例如進入空穴-電子分析功能后選擇第40個激發態后,我們選4 Show basis function contribution to hole and electron,然后輸入一個輸出閾值,比如輸入2,此時屏幕上就出現了對空穴或電子貢獻超過2%的各個基函數信息:
Basis Type Atom Shell Hole Electron Overlap Diff.
22 D 0 1(Ru) 12 23.81 % 0.00 % 0.33 % -23.81 %
23 D+1 1(Ru) 12 8.90 % 13.63 % 11.01 % 4.72 %
24 D-1 1(Ru) 12 9.06 % 25.12 % 15.09 % 16.05 %
25 D+2 1(Ru) 12 13.96 % 6.94 % 9.84 % -7.02 %
26 D-2 1(Ru) 12 14.06 % 15.57 % 14.80 % 1.51 %
27 D 0 1(Ru) 13 3.66 % 0.00 % 0.06 % -3.66 %
30 D+2 1(Ru) 13 2.32 % -0.01 % 0.00 % -2.32 %
31 D-2 1(Ru) 13 2.33 % -0.03 % 0.00 % -2.35 %
Sum of above printed terms: 78.10 % 61.22 % 16.88 %
由數據可見,對空穴產生主要貢獻的都是Ru的D基函數,我們當前用的SDD贗勢基組對Ru只描述了它的4s,4p,4d,5s電子,因此S0->S40躍遷時被激發的電子絕大部分都是Ru的4d軌道上的電子。在Ru原子上,對電子有貢獻的也都是D基函數,因此S0->S40中的MC成份對應的是Ru上面的d-d激發,這是由于Ru與配體配位后,d軌道能級發生分裂,因此出現了占據的d軌道的電子被激發到了非占據的d軌道的現象。(判斷被激發的電子所屬軌道其實也不是只有上述這一種做法,比如也可以用Multiwfn做NTO分析,然后用Multiwfn的軌道成份分析功能去考察本征值最大的那個占據的NTO的成份或者直接觀察NTO圖形。但如前所述,如果當前研究的電子激發沒法很好地通過一對NTO描述,這種做法就不靈了,而空穴-電子分析則沒有任何局限性)。
4.3 里德堡激發例子:甲醛
里德堡激發就是電子從價層占據軌道激發到彌散程度非常高的里德堡軌道的情況,在《圖解電子激發的分類》(http://sobereva.com/284)中已經介紹過。這里以甲醛為例,示例一下通過空穴-電子分析考察里德堡激發的情況。計算里德堡激發的基組必須帶有充分的彌散函數,而且應該用較高HF成份,至少是長程區域有較高HF成份的泛函,所以此例用的關鍵詞為CAM-B3LYP/aug-cc-pVTZ IOp(9/40=4) TD(nstates=10)。相應的Gaussian輸入輸出文件都在本文的文件包里。
我們按照前述過程,照常做電子-空穴分析。注意,設定格點的那一步,必須選擇-10 Set extension distance of grid range for mode 1~4來修改格點數據邊界相對于分子邊緣原子的延展距離,然后輸入一個較大的值,比如10 Bohr。因為目前版本默認的延展距離對于里德堡激發的分析來說太小,會導致里德堡軌道十分彌散的特征有很大一部分會被截斷。
當前總共算了10個激發態,下圖中把其中一些有代表性的激發態的分析結果列了出來。前四個圖都是空穴&電子圖,最后兩個圖是S0->S3激發主要牽扯到的分子軌道圖。
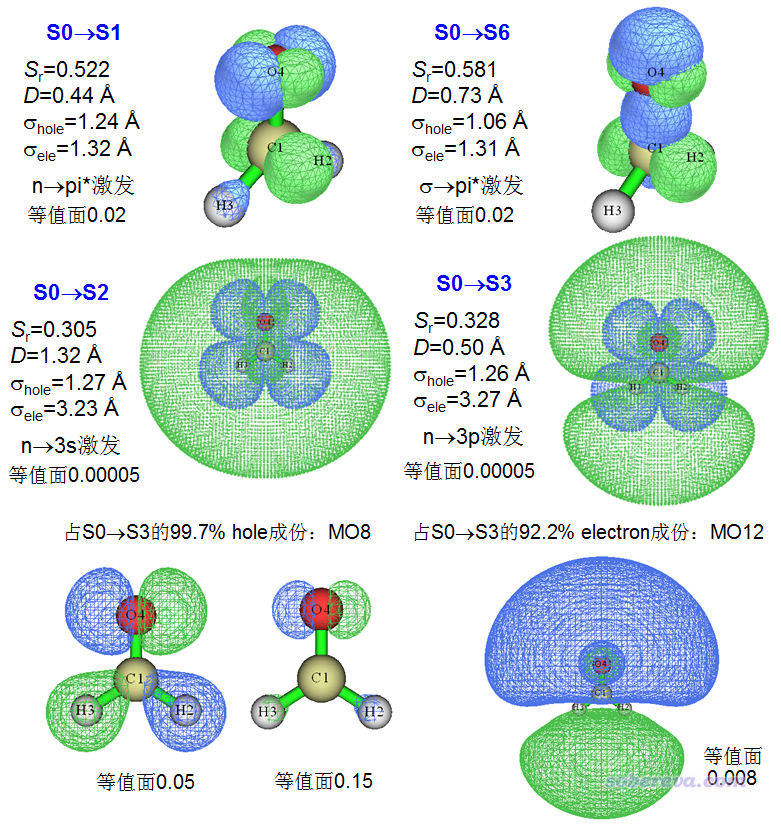
由圖可見,S0->S1和S0->S6都是普通價層激發。像這樣很小體系就無所謂局域激發和CT激發了,空穴和電子分布都有很大重疊,Sr都不算小。而且從σhole和σele指數來看,它們的空穴和電子的分布廣度也差不多。根據空穴和電子的等值面形狀,可以很容易想到主導的軌道是什么類型的,電子激發的主要特征也因此可以容易地指認。比如這兩個電子激發的電子分布都是在C和O的分子平面兩側各有一個瓣,可想而知只有pi*軌道波函數對應的模的平方才有這種分布特征。如果感覺實在判斷不出來,可以考察主導的MO的軌道等值面圖來幫助判斷。
上圖的S0->S2和S0->S3一看空穴&電子等值面圖就知道肯定是個里德堡激發,因為圖上顯示電子分布范圍非常大,已經顯著出現在了分子外圍區域,且遠遠超過空穴的分布范圍。這點也直接體現在電子的σ非常大,是空穴的σ的近三倍。從Sr上也體現出,由于空穴和電子的分布范圍差異較大,Sr的數值比較小,顯著小于S0->S1和S0->S6這樣普通價層激發的情況。注意,上圖中顯示里德堡激發的空穴&電子圖用的等值面數值很小,只有0.00005,這是因為這類激發的電子分布非常彌散,攤得非常開,如果等值面數值不這么小的話,就看不到電子對應的很彌散的等值面(可能有人覺得,對于價層激發,等值面數值用這么小的話電子的等值面照樣也會很彌散,與里德堡激發不容易區分開。但別忘了,對于普通價層激發,當你把等值面數值設得很小的時候,空穴的等值面也會同時變得非常彌散,而里德堡激發的電子的等值面彌散程度總會遠高于空穴的)。這倆里德堡激發的D指數不大,這從等值面圖上也可以大致看出,確實空穴和電子的質心位置相差不是很大。本例體現出前面提到的里德堡激發應具備的特征是:D和S都不大,而電子的σ指數遠大于空穴的。
實際上電子離域指數EDI也能充分區分價層激發和里德堡激發。價層激發S0->S1的HDI=24.8、EDI=17.0,而里德堡激發S0->S2的HDI=23.7、EDI=3.0,另一個里德堡激發S0->S3的HDI=23.9、EDI=2.8。可見里德堡激發的EDI遠遠小于價層激發。
了解里德堡激發的人,從上面給出的S0->S3的空穴&電子等值面圖上已經可以指認出激發類型了。如果判斷不出來,也可以讓Multiwfn輸出對空穴和電子貢獻最大的MO,根據MO圖形的相位,可以更容易地判斷。此激發的空穴的幾乎全部成分的是MO8,從上圖左下角的0.05等值面圖來看,既有氧的孤對電子特征,也有C-H sigma鍵特征。碰到這種難以指認的情況,可以嘗試增大等值面數值,增大到0.15之后,可以看到等值面只剩下氧的孤對電子特征了,因此MO8最主體的特征就是氧的孤對電子。對S0->S3的電子貢獻最大的是MO12,達到92.2%,可以說是絕對主導了。從其軌道圖形可見(用了較小等值面數值以使其彌散特征可以充分展現),它在分子兩側有相位相反的兩個瓣,類似p原子軌道特征,而當前分子的占據的原子軌道當中最高主量子數為2,因此MO12可以說是3p軌道。故S0->S3可以指認為n->3p型里德堡激發。而S0->S2則應指認為n->3s型里德堡激發,因為其電子分布接近球形,必然主要是s型這種幾乎球對稱的里德堡軌道主要貢獻的。
5 技巧:通過腳本批量做空穴-電子分析得到一批激發態的各種指數
將Multiwfn和Linux的shell腳本結合使用,可以輕易實現一條命令就把所有激發態的各種指數全都算出來的目的。比如,我們想把4.1節的那個D-pi-A體系的S0->S1,S2,S3激發態的各種指數全都一次性算出來,那么創建一個文本文件,比如叫batch.sh,然后把以下內容拷進去(此文件在本文的文件包里也有):
#!/bin/bash
cat << EOF > calcall.txt
18
1
D-pi-A.out
EOF
for ((i=1;i<=3;i=i+1)) #Range of excited states
do
cat << EOF >> calcall.txt
$i
1
2
0
0
1
EOF
done
./Multiwfn D-pi-A.fchk < calcall.txt |tee out.txt #Running command
rm ./calcall.txt ./result.txt -f
grep "Sr index" ./out.txt |nl >> result.txt;echo >> result.txt
grep "D index" ./out.txt |nl >> result.txt;echo >> result.txt
grep "RMSD of hole in" ./out.txt |nl >> result.txt;echo >> result.txt
grep "RMSD of electron in" ./out.txt |nl >> result.txt;echo >> result.txt
grep "H index" ./out.txt |nl >> result.txt;echo >> result.txt
grep "t index" ./out.txt |nl >> result.txt
echo
echo "Finished!"
這個腳本在《詳談Multiwfn的命令行方式運行和批量運行的方法》(http://www.shanxitv.org/612)中專門做了特別詳細的介紹。簡單來說,就是先產生一個calcall.txt文件,這里面包含了在Multiwfn里對S0->S1、S0->S2、S0->S3的空穴-電子分析所需要敲入的全部指令,其中利用到了循環,for ((i=1;i<=3;i=i+1))這個地方的i=1就是第一個激發態的序號,i<=3對應的是最后一個要算的激發態的序號。然后,腳本通過silent方式調用Multiwfn進行計算,輸出文件out.txt里包含了Multiwfn的所有輸出信息。最后用grep命令把感興趣的信息從里面全都提取出來并寫入到result.txt里。|nl用來對每批提取的信息加行號,便于與激發態序號對應(假設算的第一個態是第1激發態的話)。
把batch.sh、D-pi-A.fchk、D-pi-A.out都拷到Multiwfn所在目錄下,然后在終端里進入此目錄,運行chmod +x ./batch.sh給這個腳本加可執行權限,然后輸入./batch.sh運行此腳本。運算過程中Multiwfn的運行狀態也會在屏幕上顯示,最后屏幕上出現Finished!的時候就算完了。然后打開當前目錄下新生成的result.txt,內容如下
1 Sr index (integral of Sr function): 0.51896 a.u.
2 Sr index (integral of Sr function): 0.64906 a.u.
3 Sr index (integral of Sr function): 0.54538 a.u.
1 D_x: 0.522 D_y: 0.001 D_z: 0.001 D index: 0.522 Angstrom
2 D_x: 3.481 D_y: 0.007 D_z: 0.025 D index: 3.481 Angstrom
3 D_x: 0.574 D_y: 0.001 D_z: 0.001 D index: 0.574 Angstrom
1 RMSD of hole in X/Y/Z: 1.443 1.160 0.437 Norm: 1.902 Angstrom
2 RMSD of hole in X/Y/Z: 3.055 0.826 0.740 Norm: 3.251 Angstrom
3 RMSD of hole in X/Y/Z: 0.984 1.032 0.416 Norm: 1.486 Angstrom
略...
可見,感興趣的信息都提取出來了。大家可以根據實際需要自己修改腳本,比如可修改里面積分格點質量的設定(目前的是中等質量格點,要改的話改$i下面第二行)、對延展距離進行設定等。使用腳本實在超級方便!
如果想把每個激發態的各種格點數據分別導出也很容易。比如我們想得到每個態的密度差格點數據CDD.cub,就將上面的從$i到EOF部分的內容改為
$i
1
2
0
-1 <---- 讓導出的格點數據文件名末尾加上當前的激發態的序號
15 <---- 導出密度差格點數據
0
1
EOF
運行腳本后,比如第5個激發態的密度差格點數據就是當前目錄下的CDD_00005.cub。
6 關于Δr指數
Δr指數雖然和空穴-電子分析在計算形式上沒直接關系,但是和此文討論的問題有較大聯系,因此這里專門提一下,詳細說明見Multiwfn手冊3.21.4節。Δr是Adamo等人在J. Chem. Theory Comput., 9, 3118 (2013)中提出的,定義如下
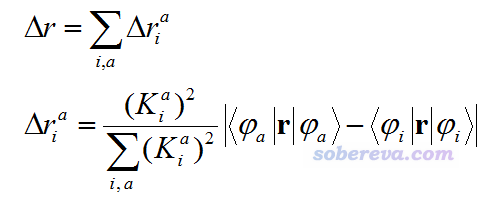
其中的K=w+w',即激發組態和去激發組態系數之和。Δr被原作者用來考察CT程度,被認為Δr越大CT程度越高。從定義上看,Δr指數的思想是每一對軌道躍遷的質心距離做權重加和,式中諸如<φ_a|r|φ_a>就相當于a軌道的質心位置,而|<φ_a|r|φ_a>-<φ_i|r|φ_i>|就相當于i與a軌道間躍遷對應的軌道質心距離,而前頭的K^2/∑K^2項就相當于i-a軌道躍遷在電子激發中的權重。
從物理意義上看,其實Δr指數和D指數比較接近,本質上都是衡量空穴和電子的質心距離,但D指數的計算形式是嚴格的,而Δr指數的物理意義則沒那么好,而且也沒考慮到組態函數之間的耦合,因此一般沒必要用Δr指數指數。當你發現D指數和Δr指數有明顯沖突的時候,也應當以D指數為準。但Δr指數有一個好處是計算非常快,而且在Multiwfn中可以一次對一大批激發態計算出來,都不需要利用腳本,而且Δr指數還可以分解為軌道躍遷的貢獻,這在上面的公式中已經體現了。
在Multiwfn中計算Δr指數指數所需的輸入文件和空穴-電子分析完全一樣。比如對4.1節的D-pi-A體系,要計算Δr指數,就在Multiwfn啟動后輸入如下命令:
D-pi-A.fchk
18
4 //計算Δr指數
D-pi-A.out
1-5 //要計算的激發態序號。1-5代表計算S0到所有5個激發態
結果如下,瞬間就算出來了,Δr單位是距離,以兩種單位分別輸出
Excited state 1: Delta_r = 4.607326 Bohr, 2.438092 Angstrom
Excited state 2: Delta_r = 9.456166 Bohr, 5.003988 Angstrom
Excited state 3: Delta_r = 4.075887 Bohr, 2.156867 Angstrom
Excited state 4: Delta_r = 3.940624 Bohr, 2.085289 Angstrom
Excited state 5: Delta_r = 2.776245 Bohr, 1.469126 Angstrom
通過對比可以發現,對當前體系,Δr和D指數確實存在正相關性,體現出二者的內在特征的相似性;而Δr和Sr指數則基本沒有相關性,畢竟它倆在定義上沒有明顯相似之處。
如果選擇要考察的激發態序號的時候只選擇了一個軌道,Multiwfn就可以把Δr分解為各個軌道對的貢獻,這在某些情況下可以把問題研究更得深入。例如對上述D-pi-A體系,選擇要考察的激發態序號的時候輸入4選擇激發態S4,然后屏幕上輸出Δr指數后會問你是否輸出軌道對的貢獻,此時輸入y,然后輸入顯示閾值,這里輸入0.01,程序就把對Δr指數貢獻超過0.01埃的都輸出出來了,如下所示:
#Pair Orbitals Coefficient Contribution (Bohr and Angstrom)
2516 52 57 -0.1175600 0.1053200 0.0557330
2517 52 59 -0.0438400 0.0364131 0.0192690
2592 53 57 0.1450600 0.2444716 0.1293688
2785 56 57 0.6318800 8.7878820 4.6503472
2787 56 59 -0.1128900 0.1361715 0.0720588
其中#Pair是相應軌道躍遷對應的單激發組態函數的序號,不用管。由數據可見,之所以S0->S2的Δr高達5.00埃,主要是因為56與57軌道之間的躍遷(顯然分別對應HOMO和LUMO)貢獻了多達4.65埃。
7 關于Λ指數
最早提出的,而且也是目前使用得很多的考察電子激發特征的指數是J. Chem. Phys. 128, 044118 (2008)中提出的Λ指數,Δr指數其實就是在上面做了雞毛蒜皮的修改。Λ指數和Δr指數形式極其相似,把Δr指數中的|<φ_a|r|φ_a>-<φ_i|r|φ_i>|項替換為∫|φ_a||φ_i|dr(相當于衡量a,i兩個軌道的重疊程度)就是Λ指數。Multiwfn中的主功能18的子功能14可以計算Λ指數,計算過程和Δr指數指數如出一轍,就不在這里示例了,手冊4.18.4節有例子,在手冊3.21.14節里有詳細說明。
Λ指數的計算比Δr更耗時,因為其中牽扯到的軌道波函數模的乘積的積分需要通過數值格點方式來積分。但Multiwfn中計算Λ指數的功能已經做了最大程度的優化,因此對大體系的實際耗時還是完全可以接受的。如果認為Δr是D的“劣化”版,那么可以將Λ指數視為是Sr指數的“劣化”版。從本質上看,Λ指數和Sr指數都是對空穴與電子重疊程度的體現,但Λ指數并沒有Sr指數在定義上那么嚴格,而且也忽視了組態間的耦合。凡是Λ指數和Sr指數存在沖突的情況,也都應當用Sr指數說事。
正如同D和Sr指數存在明顯的互補作用,對實際問題分析缺一不可,倘若你有特殊原因非要用Δr和Λ來說事,也不要只使用其一,最好結合使用,以便對電子激發特征了解得更全面。
還有其他一些人提出的各種各樣的表征電子激發的特征指數,比如J. Chem. Theory Comput., 10, 3896 (2014)提出的φs指數。由于Multiwfn里支持的考察電子激發特征的指數已經足夠充分了,已經可以把電子激發研究得極盡透徹了,因此我就不再打算在Multiwfn里加入亂七八糟沒多大用處的其它的指數了。
8 總結
本文全面、系統地介紹了Multiwfn中強大的空穴-電子分析功能,仔細閱讀過本文的讀者應該已經認識到這對于考察電子激發問題是必不可少的利器,可以把電子激發特征從各個角度一覽無余地剖析透徹,既能給出詳實的定量數據,又能給出漂亮的吸引眼球的圖像。本文雖然只用了三個簡單體系舉例,就已經討論出相當多的信息了,而且這還僅僅是Multiwfn支持的全部電子激發分析方法中的一部分。可見,經常研究電子激發問題的人,若充分靈活運用Multiwfn,特別是空穴-電子分析,還愁文章里沒得討論?