電子激發過程中片段間電荷轉移百分比的計算

電子激發過程中片段間電荷轉移百分比的計算

文/Sobereva @北京科音

First release: 2017-Dec-15   Last update: 2022-Mar-15

1 前言

電子激發過程往往伴隨著電子分布范圍的明顯轉移，在一些文獻里經常給出電子躍遷過程中某片段向另一個片段電荷轉移特征的百分比，CT%。比如對于配合物體系，很常見的躍遷模式是Metal-to-ligand charge transfer (MLCT，金屬向配體的電子轉移），許多研究此類體系的文章都給出基態向各個激發態的MLCT(%)。經常有人問怎么計算這個，其實很簡單，本文就以下圖所示的W(CO)4(phen)作為實例演示一下。本文提到幾種不同方法，如果你著急算出來的話，直接看第5節用IFCT分析即可，這是最簡單也最理想的，其它方法都可以不用考慮。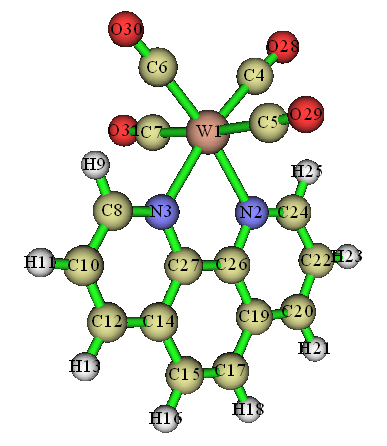

本文的計算和分析分別使用Gaussian 16 A.03和Multiwfn官網上的最新版本完成，后者可在其主頁http://www.shanxitv.org/multiwfn上免費下載，入門貼看《Multiwfn入門tips》（http://www.shanxitv.org/167）。文獻里常用“電荷轉移”這個詞，為了與習俗相同，下文也用這個詞，但為了避免誤解，這里明確一下：在本文中說A向B的電荷轉移，一律等價于說A向B的電子轉移。本文討論的都是單電子激發（TDDFT基本也只能描述這個），雙電子激發的情況不屬于本文范疇。

本文涉及的輸入輸出文件可以在這里打包下載：file.rar。結構已在B3LYP下對配體用6-31G*、對W用SDD優化過。

2 基于原子電荷計算電荷轉移百分比

設體系被分為兩個片段A、B，則電子激發過程中片段A向片段B的電荷轉移百分比可以這樣計算：
其中GS和EX分別代表基態和激發態，諸如q(A,EX)就代表某個激發態時片段A的電荷，它可以通過將這個片段里所有原子的原子電荷的加和得到。顯然，如果激發前后，片段A的電荷變化為0，則q(A→B)=0%；如果激發時片段A恰好把一個電子轉移給了其它區域，即片段B，那么q(A→B)=100%。如果算出來是負值，顯然就是代表電子激發時電子從片段B轉移給了片段A。

原子電荷的計算方法很多，見《原子電荷計算方法的對比》（http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml）。一般來說，用常用的ADCH、Mulliken、NPA、CHELPG電荷來計算電荷轉移百分比都可以，定量上肯定會有些差異。下面例子用的是筆者在J. Theor. Comput. Chem., 11, 163 (2012)提出的ADCH電荷，通過Multiwfn來計算。Multiwfn計算原子電荷時可以很方便地定義片段，片段電荷可以一下子就得到，免得手動去加和了。

W(CO)4(phen)的基態是單重態，首先對它進行計算，從而得到記錄基態波函數信息的S0.chk。輸入文件內容如下。考慮到此體系涉及電荷轉移激發，用了適合此類問題的CAM-B3LYP。注意基態和激發態用的計算級別必須相同，否則之后對兩個態間片段電荷求差將無意義。（本文用的是Gaussian16，默認是int=ultrafine，用這么高積分格點完全沒必要，所以額外寫了int=fine降低耗時）
%chk=S0.chk
#P CAM-B3LYP/genecp int=fine

B3LYP/6-31G* with SDD opted

0 1
[坐標]

C O N H
6-31G*
****
W
SDD
****

W
SDD


然后再做TDDFT電子激發計算，這里假設我們要考察第二單重激發態（S2）的電子分布情況，所以root=2，并且通過out=wfn density把S2的自然軌道寫到.wfn文件里（對這部分不懂的人看《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》http://www.shanxitv.org/314和《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》http://www.shanxitv.org/379）。輸入文件如下：
#P CAM-B3LYP/genecp int=fine out=wfn TD(root=2) density

B3LYP/6-31G* with SDD opted

0 1
[坐標]

C O N H
6-31G*
****
W
SDD
****

W
SDD

S2.wfn


下面，我們計算一下S0→S2的MLCT百分比。此時金屬自身就是一個片段，所以不需要在計算前先定義片段。先計算S0態的原子電荷，啟動Multiwfn，依次輸入
S0.fchk    //通過formchk將S0.chk轉換得到
7   //布居分析與原子電荷計算
11  //ADCH電荷
1  //用程序內置的球對稱化的自由原子密度
W的基態的ADCH電荷為-0.053069。

重新啟動Multiwfn，載入S2.wfn，之后的步驟同上，得到W的S2態的ADCH電荷為0.212891。因此，S0→S2的MLCT百分比為[0.212891-(-0.053069)]*100%=26.6%。

Gaussian輸出文件里默認輸出了Mulliken電荷（用Multiwfn也可以計算），基態時W是-0.214470，S2態是0.094357，對應MLCT百分比為30.9%。可見，雖然Mulliken電荷和ADCH電荷原理相差甚巨（后者可靠度通常更高），但計算的MLCT百分比倒是定性相符。不過如果用Hirshfeld電荷來計算，MLCT百分比只有16.7%，明顯偏低，筆者不太推薦用Hirshfeld電荷討論電荷轉移量問題。

我們可以把體系進行任意劃分，得到電子躍遷中兩個片段間的電荷轉移百分比。比如，我們把W(CO)4作為一個片段，phen作為另一個片段進行考察。先計算S0態的W(CO)4部分的原子電荷，啟動Multiwfn依次輸入
S0.fchk
7   //布居分析與原子電荷計算
-1  //定義片段
1,4-7,28-31   //W(CO)4部分的原子編號
11  //ADCH電荷
1   //用程序內置的球對稱化的自由原子密度
程序在輸出原子電荷之后，還輸出了片段電荷，為-0.490847。以相同的方式，對S2.wfn再做如上操作，得到S2態W(CO)4的片段電荷為0.020310。因此，此激發中W(CO)4→phen的百分比為51.1%。這數值明顯大于前面看到的MLCT百分比。因此暗示著，S0→S2的過程，不僅有W→phen的MLCT，還有顯著的(CO)4→phen的Ligand-to-ligand CT (LLCT)特征。但是，我們不能把(CO)4→phen的百分比簡單估計為51.1%減去前面得到的MLCT百分比26.6%，因為W和(CO)4之間也有電荷轉移。

為了更好地理解上面計算出的數據，我們可以用S2.wfn和S0.fchk對S2和S0之間繪制電子密度差圖，步驟在這里有詳細介紹：《使用Multiwfn作電子密度差圖》（http://www.shanxitv.org/113），結果如下。綠色和藍色分別代表電子激發后電子增加和減少的部分，等值面數值為0.004。

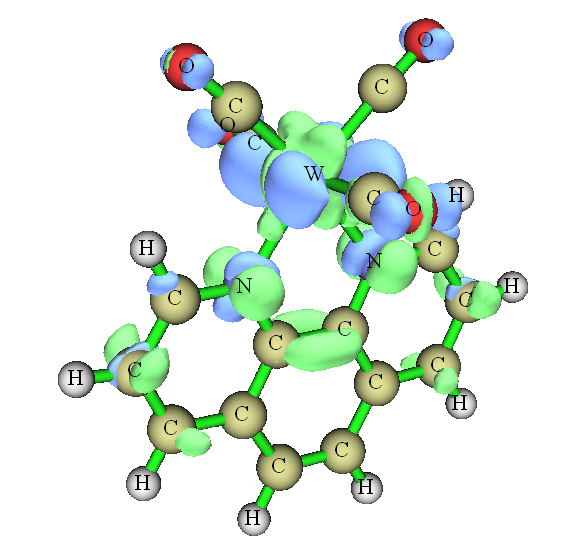
雖然從此圖上不太便于定量考察，但整體上可以看出，躍遷導致phen部分電子密度增加，而W和(CO)4部分電子密度都有所降低，這和前面的定量數據結論相符。

3 通過考察軌道成份計算電荷轉移百分比

上一節是從片段電荷量的凈變化角度進行考察，這一節通過軌道的角度考察電荷轉移百分比。一般我很不建議用這一節的做法，主要在于電子激發不可能被一對軌道躍遷完美地描述，因此不管考察哪一對軌道來計算電荷轉移百分比都不是嚴格的。即便借助NTO分析，貢獻最大的NTO軌道對的貢獻量偏離100%往往還是不可忽略的。因此本節的做法不是普適的，讀者了解一下就行了。

上面考察的S0→S2的激發，從Gaussian輸出文件看幾乎完全對應于MO80→MO83的激發，貢獻達到96.6%（不會算者看此文《電子激發任務中軌道躍遷貢獻的計算》http://www.shanxitv.org/230），因此也可以直接通過分析MO80和MO83的軌道成份來討論電荷轉移百分比。這兩個軌道圖形如下（等值面數值=0.05）：

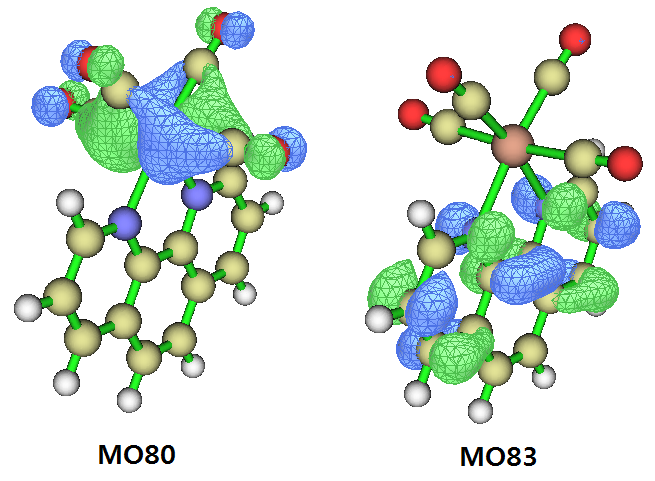
按照《談談軌道成份的計算方法》（http://www.shanxitv.org/131）里的步驟，我們用Multiwfn對S0.fchk記錄的軌道通過Hirshfeld方法進行軌道成分分析。MO80和MO83當中W的貢獻分別是47.1%和2.8%，因此，我們可以說此體系的MLCT百分比為47.1%-2.8%=44.3%（如果用Mulliken方式計算軌道成份，結果為60.7%-3.6%=57.1%）。

肯定有人深感困惑，上一節的方法算出來的MLCT百分比不算特別大，怎么這回算出來的結果這么大？差異實際上來自于非弛豫密度和弛豫密度的差別。按照Gaussian輸出文件里軌道躍遷和組態系數，直接構建的激發態密度叫做非弛豫密度(non-relaxed density)，這可視為實際激發態密度的最低階近似，或者可以認為這是電子激發一瞬間的激發態密度。而弛豫密度，姑且可以視為之后經過電子密度進一步重排，達到穩定狀態的密度，更接近實際情況。在Gaussian里，直接用density關鍵詞默認給出的激發態密度是弛豫密度，產生弛豫密度耗時是比較高的，比做普通TDDFT計算本身要高非常多。若我們將MO80和MO83的分布圖，與上一節繪制的基于弛豫的激發態密度得到的密度差圖進行對比，也可以看出弛豫和非弛豫密度的差別。MO83完全是在phen配體上，在W上沒有任何分布，而從基于弛豫密度的密度差圖上看，電子激發時W的附近有的地方電子密度降低，而有的地方密度則增加。因此考慮了激發態密度弛豫效應時，電子從W到phen的凈轉移量沒那么大。如果你想用上一節方式考察電荷轉移問題，但又想用非弛豫密度，那就把density后面寫上=rhoci即可（我的觀點是，基于弛豫密度和非弛豫密度討論都可以，至少同一篇文章里必須統一。不想花額外時間產生弛豫密度就通過非弛豫密度下的原子電荷、密度差討論，或者通過軌道討論）。

我們還可以考察(CO)4到phen的LLCT百分比。我們需要計算一下MO80中(CO)4的成份。令Multiwfn載入S0.fchk，然后執行下述操作即可：
8  //軌道成份分析
8  //Hirshfeld方式計算軌道成份
1
-9  //定義片段
4-7,28-31
80  //軌道編號
得到(CO)4對MO80貢獻為47.2%。然后輸入83，得到(CO)4對MO83貢獻為5.8%。因此，S0→S2的激發中(CO)4→W(phen)的特征百分比是47.2%-5.8%=41.4%。由于W在MO83中的貢獻僅有2.8%，可忽略不計，因此，我們可認為(CO)4→(phen)的LLCT百分比大約是41%。（我們不能簡單地從41.4%中減去2.8%作為準確的LLCT百分比，因為MO83中W的2.8%對應的電子也可以是來自于W自身的）

通過軌道方式討論S0→S2比較容易，因為此時只有一對MO產生了不可忽視的貢獻。但是，很多電子態的躍遷需要通過多對MO躍遷才能較好描述，這就得考慮許多對MO了，會十分麻煩。好在多數此類情況，可以將MO轉化為NTO來解決，見《使用Multiwfn做自然躍遷軌道(NTO)分析》（http://www.shanxitv.org/377）。如果發現只有一對NTO產生絕對的主導，那么只要分析這兩個NTO的成份，就可以按上述方式討論片段間電荷轉移百分比。

另外順帶一提，有些文獻、書籍里描述電荷轉移問題很粗糙。我們如果把軌道等值面數值提升到0.015，那么看到的MO80是這樣的：

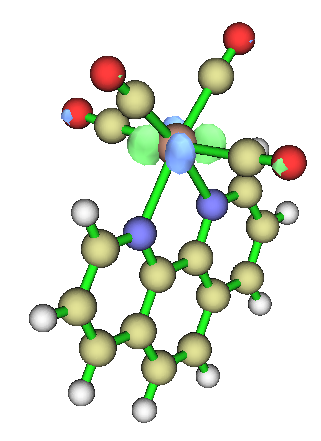
根據化學常識，可以知道這對應的是W的d軌道。于是，有人會說S0→S2就是W的d電子向phen配體的激發。根據上面的討論，可以知道這種說法非常粗劣，因為我們通過計算看到，LLCT和MLCT特征百分比都有40%出頭，描述時忽略任意一種都是明顯不恰當的！

4 通過空穴-電子分析考察電荷轉移百分比

使用Multiwfn強大、直觀的空穴-電子分析計算電荷轉移百分比非常嚴格，對任何體系都是普適的，詳見《使用Multiwfn做空穴-電子分析全面考察電子激發特征》（http://www.shanxitv.org/434），里面的4.2節通過配合物實例介紹了怎么利用空穴-電子分析給出的數據考察電荷轉移百分比。簡單來說，你需要計算某片段在空穴和電子分布中各自占的百分比，然后求差后取絕對值再乘以100%。

5 通過IFCT分析考察電荷轉移百分比

這是最理想且最方便的計算電荷轉移百分比的方法。如果你使用2022-Mar-15及以后更新的Multiwfn版本，按照《在Multiwfn中通過IFCT方法計算電子激發過程中任意片段間的電子轉移量》（http://www.shanxitv.org/433）中的方法用Multiwfn做完IFCT分析后，在屏幕上直接就給出了CT(%)和LE(%)，省事至極！計算原理請讀者看Multiwfn手冊3.21.8節中On the evaluation of CT%部分的說明。而且這個方法可以用于包含任意多個片段的情況，而不像前文其它方法那樣只能用于兩個片段。而對于只有兩個片段的情況，IFCT分析會給你intrinsic CT(%)和apparent CT(%)兩種方式定義的電荷轉移百分比，區別和定義在手冊里也都說了。簡單來說，intrinsic CT(%)體現的是內在的電荷轉移百分比，體現的是真實參與了電荷轉移的電子量，沒有納入A→B和A←B片段間兩種方向電子轉移造成的抵消，是只有靠IFCT方法才能得到的物理意義非常強的CT%的定義；而apparent CT(%)可以認為是表觀的電荷轉移百分比，是基于凈轉移電荷量計算的，已考慮了不同方向電子轉移產生的抵消效應，和前文那些方法在本質上相一致，且結果和第4節介紹的方法精確相同。通常不太可能電荷轉移在你定義的兩個片段間是嚴格單方向的，顯然此時intrinsic CT(%)比apparent CT(%)更大。

最后，還要強調一點，不管你用哪個方法算CT%，其結果都是直接依賴于片段的定義的，因為這體現的是你定義的片段間的電荷轉移情況。假設你把整個體系就定義為一個片段，那么所有激發態的CT%則都精確為0。