圖解電子激發的分類

圖解電子激發的分類

First release: 2015-Mar-9 Last update: 2018-Sep-8

電子垂直激發涉及許多類型。經常有人問怎么判斷電荷轉移激發，怎么指認激發類型等等，這個帖子就通過實例和圖形進行介紹。

1 概述

電子激發有不同分類方式。對于UV-Vis光譜涉及的電子激發范疇，可以分為兩大類
(1)價層激發：電子從價層占據軌道激發到價層空軌道。這里說的價層軌道是指由價層原子軌道混合構成的分子軌道。
(2)里德堡激發：電子從價層占據軌道激發到里德堡軌道。里德堡軌道是指那些分布十分彌散的空軌道。這樣的軌道通常不表現出分子軌道特征，而是整體形狀表現出類似原子軌道的特征，這在后文將通過圖形進行展示。

價層激發又可以進一步劃分。從電荷怎么轉移的角度分，可以分為
(1)局域激發(Local excitation, LE)：電子被激發前后其分布區域沒有明顯變化。雖然名字叫“局域”，但并非激發涉及的區域只能局限在體系的某個局部。比如電子被激發前后其分布范圍都覆蓋整個體系，也算局域激發，
(2)電荷轉移激發(Charge-transfer excitation, CT)：電子被激發后分布區域發生了明顯轉移。既可以在分子內轉移，也可以在分子間轉移。
某些類型的體系的LE和CT還可以進一步劃分，比如過渡金屬配合物，LE激發可分為metal-centered transition (MC)、intraligand或ligand-centered transition (LC)。CT激發可以分為metal-to-metal charge transfer (MMCT)、ligand-to-ligand charge transfer (LLCT)、metal-to-ligand charge transfer (MLCT)、ligand-to-metal charge transfer (LMCT)。比如其中MLCT就代表被激發的電子是從金屬向配體轉移。

價層激發從軌道特征上也可以進行劃分。對于主族原子，電子可以從占據的sigma、pi、n（雜原子提供的孤對電子）軌道激發到反鍵軌道sigma*和pi*。含pi電子和雜原子的有機分子是最常見的研究對象，其UV-Vis光譜感興趣的范疇內主要出現的是pi->pi*和n->pi*，這是能量最低的兩類激發。sigma->pi*和n->sigma*能量往往高一些。對于沒有雜原子和pi電子的，比如烷烴，顯然就只有sigma->sigma*了，由于sigma是能量較低的占據軌道，sigma*是能量較高的空軌道，所以這種類型激發能很高。對于過渡金屬原子，d軌道也會參與，比如d-d、d-p金屬內激發。

軌道特征和電荷轉移方式這兩種劃分價層激發的方式并不矛盾。例如常見的pi->pi*和n->pi*都既有屬于LE激發的情況也有屬于CT激發的情況。

電子激發實際上是電子態的躍遷，如果用軌道躍遷來描述則通常需要涉及到許多軌道對兒，各占一定成分。可以計算各個軌道對兒躍遷的貢獻，見《電子激發任務中軌道躍遷貢獻的計算》（http://www.shanxitv.org/230）。如果某個軌道對兒的貢獻占絕對主導性，比如大于75%，那么可以通過分析這兩個軌道的特征來判斷激發的類型。如果沒有哪個軌道對兒占絕對主導性，則需要通過別的方法進行考察。比如Multiwfn（http://www.shanxitv.org/multiwfn）支持的electron-hole分析可以給出electron和hole的分布圖，電子躍遷可以認為是從hole區域躍遷到electron區域，見《使用Multiwfn做空穴-電子分析全面考察電子激發特征》（http://www.shanxitv.org/434），這個功能可以直接支持Gaussian輸出文件作為輸入。或者也可以做NTO分析，此方法對多數情況可以將電子態躍遷近似轉化為單個NTO對兒的躍遷，見《使用Multiwfn做自然躍遷軌道(NTO)分析》（http://www.shanxitv.org/377）、《躍遷密度分析方法-自然躍遷軌道(NTO)簡介》（http://www.shanxitv.org/91）。

PS：電子激發計算方法的選用在此文有詳細討論：《亂談激發態的計算方法》（http://www.shanxitv.org/265），這里對關鍵幾點著重強調一下。CT激發和里德堡激發都有個共同的特點，就是被激發的電子在激發前后分布范圍變化很大，或者說electron和hole重疊得比較小。對于這種情況，必須用范圍分離泛函（如wB97XD），或至少是HF成份比較高的泛函（如M06-2X），方可得到合理的結果。對于里德堡激發的計算，所用基組必須有充足的彌散函數，如aug-cc-pVDZ，否則顯然沒法合理描述里德堡激發涉及的分布十分彌散的空軌道。

下面就通過各種實例用圖像直觀地展示各種類型的激發，并且著重說明怎么判斷激發的類型。第二節涉及的是價層激發，第三節涉及的是里德堡激發，第四節討論一下價層激發和里德堡激發間的關系。計算由Gaussian09完成，軌道圖形皆由Multiwfn繪制（詳見《使用Multiwfn觀看分子軌道》 http://www.shanxitv.org/269），若未注明軌道等值面數值皆為默認的0.05。

2 價層激發

2.1 局域激發與電荷轉移激發

這里用N-苯基吡咯來說明LE和CT激發（為便于示例討論，沒有取極小點結構，而是平面的過渡態結構）。在cam-b3lyp/6-31+g(d)下做TDDFT計算，S0->S1躍遷輸出為
Excited State   1:      Singlet-A1     5.0615 eV 244.96 nm f=0.3935 <S**2>=0.000
      36 -> 40        -0.10127
      37 -> 40        -0.12755
      38 -> 39         0.67269
其中38號軌道（HOMO）向39號軌道（LUMO）貢獻達到90%，占絕對的主導性，因此這里可以直接通過這兩個軌道來判斷激發類型。下圖左側是結構示意圖，中間是HOMO，右側是LUMO。

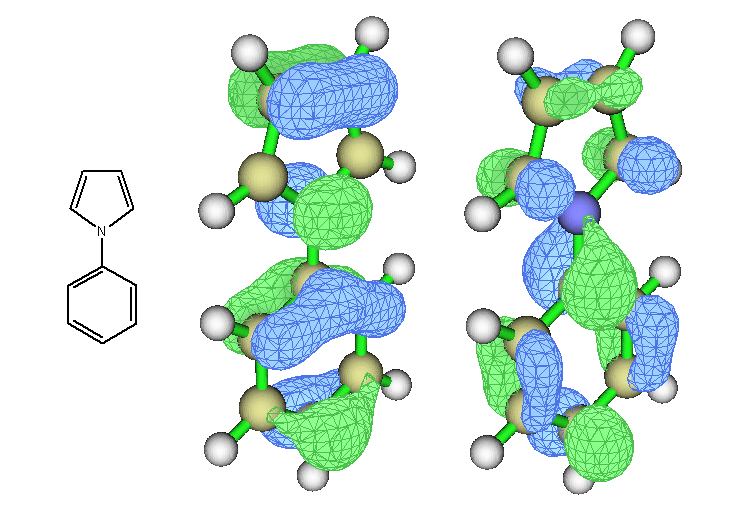
可見，HOMO和LUMO都是整體分布的，因此從HOMO向LUMO躍遷并不會令電子分布有明顯的轉移趨勢，所以S0->S1是局域激發。

再看S0->S5的輸出
Excited State   5:      Singlet-A1     5.9669 eV 207.79 nm f=0.1674 <S**2>=0.000
      37 -> 40         0.69064
      38 -> 39         0.13261
其中MO37->MO40貢獻達到95%，因此也可以只看這兩個軌道來討論激發的特征，這兩個軌道分別如下所示

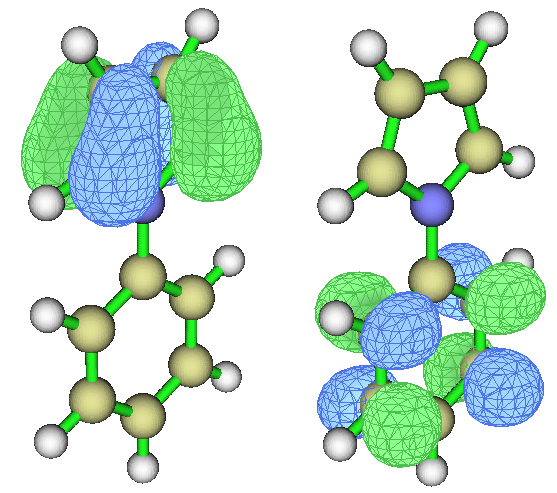
可見37號軌道分布在吡咯上，而40號軌道分布在苯基上，因此S0->S5是個十分明顯的CT躍遷，激發過程中電子從吡咯向苯基轉移。

由于上述兩個激發都有占絕對主導的軌道對兒躍遷，因此用Multiwfn的electron-hole分析得到的結論與直接觀看軌道圖形十分相似，如下所示，圖片取自Multiwfn手冊4.18.1節的例子。綠色代表electron分布，藍色代表hole分布，這種圖表示電子從藍色區域激發到綠色區域。

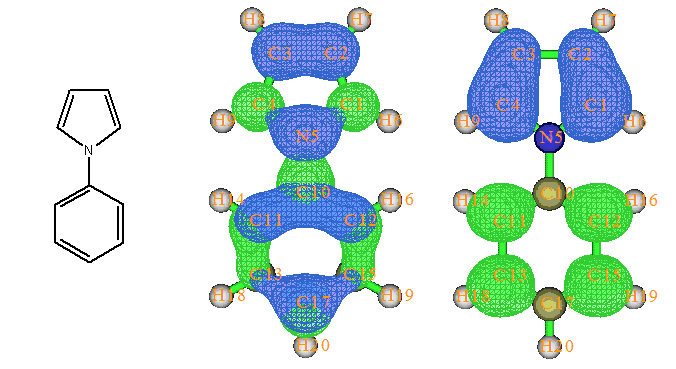
但是有的激發，比如S0->S2，如下所示沒有主導的軌道對兒。雖然MO38->MO40貢獻是最大的，66.7%，但是只考慮它而忽略了其它軌道則容易造成判斷不可靠，因此這個激發不適宜通過分子軌道來分析。
Excited State   2:      Singlet-B2     5.0739 eV 244.36 nm f=0.0139 <S**2>=0.000
      35 -> 40         0.14847
      36 -> 39         0.32214
      36 -> 46         0.10308
      37 -> 39         0.15255
      38 -> 40         0.57770
而利用Multiwfn，不管有多少軌道對兒有不可忽略的貢獻都沒關系，都能轉換成electron和hole分布，一目了然，如下所示

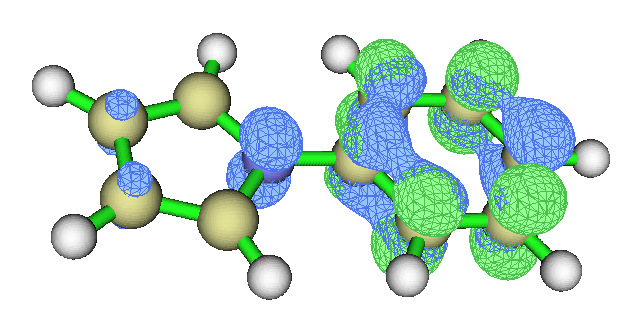
可見hole大部分出現在苯基區域，很少一部分出現在吡咯區域，而electron完全出現在苯基區域。由此可知電子躍遷后會有一點電子從吡咯流向苯基，有那么點CT特征，但是總的來說，還是LE特征更主要，因此適合歸屬為LE激發。

Multiwfn的electron-hole模塊超級強大，不僅如上所示可以給出electron和hole分布，還可以做很多分析幫助判斷CT程度，比如electron和hole質心的距離、electron與hole的重疊積分、繪制密度差圖（即electron分布減去hole分布）、把electron和hole轉換成更易于考察的平滑分布形式、軌道或片段對electron和hole的貢獻等等。Multiwfn還能做很多重要的其它電子激發分析，如把振子強度分解為軌道對/基函數/原子的貢獻、繪制躍遷密度和躍遷偶極矩密度、考察電子激發過程中片段間的電荷轉移細節、計算衡量CT距離的Δr指數等，這里就不多談了，感興趣者參見《Multiwfn支持的電子激發分析方法一覽》（http://www.shanxitv.org/437）。

上面的CT是分子內的，下面我們看一個分子間CT激發的例子。此例Be和F2擺成T型，其能量最低的激發是Be的2s電子向F2反鍵sigma軌道發生電荷轉移躍遷，100%由HOMO->LUMO所貢獻，兩個軌道圖形分別如下所示。

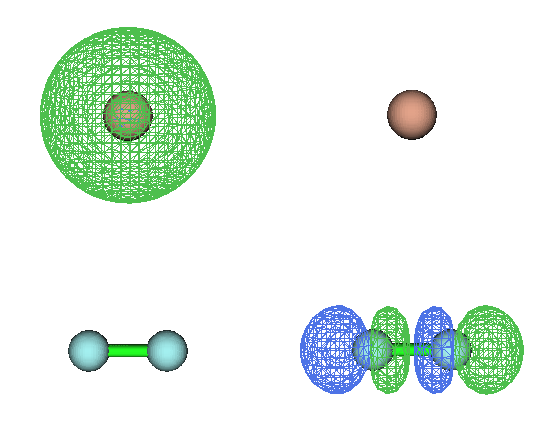
可見此激發完全全將一個電子從Be轉移到了F2上。此例注意F2的鍵長被人為拉長為了1.415埃以使得其反鍵sigma軌道能量比平衡結構下低得多，否則最低能量激發將對應于Be向自己的2p激發。

2.2 不同軌道特征的激發

這一節對幾種常見的電子激發類型進行示例。若有人對sigma、pi、孤對電子，以及成鍵、反鍵軌道這些最基礎的概念尚不明白的話，建議先看看結構化學書里的基礎知識。

我們算一個簡單的體系，環丙烯。在b3lyp/6-311g(d,p)下優化，然后用PBE0/def2-TZVP做TDDFT計算，前兩個態輸出如下
Excited State 1: Singlet-B2 6.4794 eV 191.35 nm f=0.0697 <S**2>=0.000
11 -> 12 0.69254

Excited State 2: Singlet-B1 6.5549 eV 189.15 nm f=0.0011 <S**2>=0.000
10 -> 12 0.70538

可見其中只涉及到環丙烯的MO10、11、12，軌道圖形如下

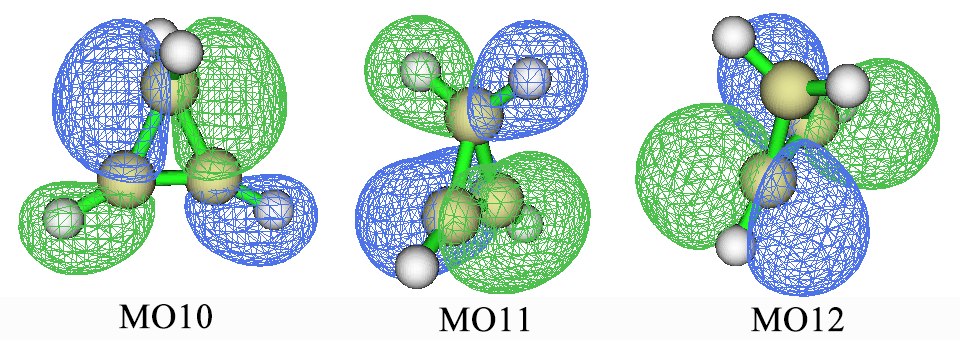
判斷是什么類型激發前先要指認軌道類型。分子軌道往往有高度離域性、同時展現不同區域的不同特征，指認的時候要考慮主要特征而忽略次要特征。由上圖可見，MO10是兩個C-C sigma鍵的成鍵軌道，同時對C-H之間sigma鍵也有貢獻，所以毫無疑問應該指認為sigma軌道。MO11主要表現的是C=C鍵的pi軌道，因為沿著鍵軸有個節面。雖然它也對亞甲基的C-H sigma鍵有貢獻，但這里就忽略這個次要特征了，就當MO11是pi軌道了。MO12顯然是C=C鍵的反pi（pi*）軌道，因為不僅沿著鍵軸有個節面，在垂直于鍵軸上也有個節面。因此，對于當前計算，第一激發態是pi->pi*激發，第二激發態是sigma->pi*激發。

下面一個例子是丙酮，這是B3LYP/def2TZVP下優化然后用B3LYP/aug-cc-pVTZ做的TDDFT計算。這個例子下一節將用來作為例子討論里德堡激發，在這一節我們只討論它的最低階激發，是個典型的價層激發，如下所示：
Excited State   1:      Singlet-A2     4.4326 eV 279.71 nm f=0.0000 <S**2>=0.000
      16 -> 17         0.69737
      16 -> 20         0.10527
由于16->17（即HOMO->LUMO）激發占了將近100%的成份，就不考慮16->20了。為指認其激發類型，我們看看16、17號軌道的特征，如下所示

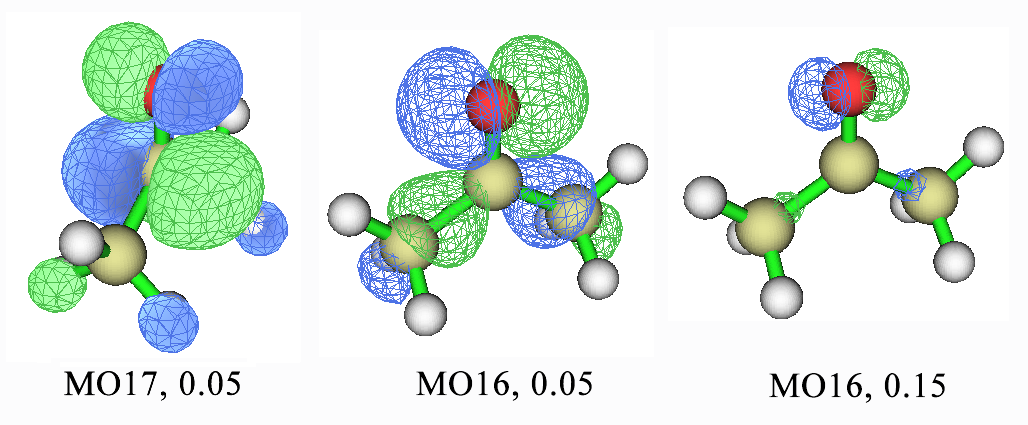
圖中標注的小數是軌道等值面數值，在Multiwfn中默認是0.05。可見MO17是典型的pi*軌道。但在默認等值面數值下，MO16的特征指認起來看似有點困難（上圖的中間那個），既有氧的孤對電子特征，也有C-C成鍵特征，此時如何指認？解決辦法是逐漸增加等值面數值，增加到0.15后，圖像如上圖右側所示，基本上只在氧的兩側有等值面了，也就是說這個軌道的孤對電子特征占其主要成分。因此丙酮的這個第一激發態應當指認為n->pi*躍遷。（可能有人會問為什么MO16 0.15的圖會看出是孤對電子，原因是很簡單：從等值面上看這既不是pi，也不是sigma，而是電子分布懸在氧的兩邊沒干活兒，顯然是沒有配對兒的氧的孤對電子軌道）

再看這一節最后一個例子，吡嗪。這是在PBE0/def2-TZVP下做的TDDFT計算。我們考察以下幾個激發
Excited State 1: Singlet-B3U 3.9808 eV 311.46 nm f=0.0044 <S**2>=0.000
21 -> 22 0.70620

Excited State   3:      Singlet-B2U    5.4867 eV 225.97 nm f=0.1000 <S**2>=0.000
      18 -> 23        -0.23669
      20 -> 22         0.66566

Excited State 5: Singlet-B1G 6.5598 eV 189.00 nm f=0.0000 <S**2>=0.000
19 -> 23 0.70626

其中涉及的軌道圖形如下。由于S0->S3激發中18->23的貢獻僅有10%，就無視了。

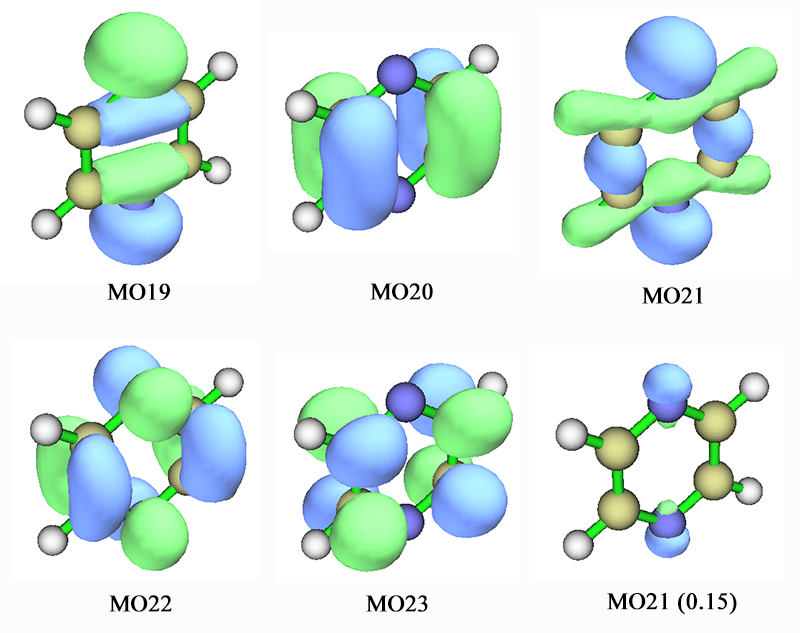
MO21看起來比較復雜，也是既表現出成鍵也表現出孤對電子特征，但是把等值面數值調大到0.15后，如上圖右下所示，只有氮原子旁邊有等值面出現了，說明此軌道整體來說可指認為氮的孤對電子軌道。注意雖然MO22對于左側和右側兩個碳原子間的pi鍵有貢獻，但是MO22是空軌道，而且在C-N之間表現反鍵特征，所以還是要將之指認為pi*。現在知道了MO21和MO22的類型，我們也就知道S0->S1是n->pi*激發了。

S0->S3是20->22主導的。MO20明顯是pi軌道，因此這個激發是pi->pi*激發。

19號軌道比較明顯地表現出氮的孤對電子特征，若把等值面數值增大到0.15后，也是像MO21一樣只在氮原子上面有等值面。MO23毫無疑問是pi*，因此S0->S5是n->pi*激發。

3 里德堡激發

前面提到，里德堡激發會將電子激發到很彌散的里德堡軌道上，這些軌道的形狀和原子軌道有一定相似性，因此討論里德堡激發時，經常會看到諸如n->3pz的表示。這里3pz就是指電子激發后所處的里德堡軌道的形狀類似于pz，并且其主量子數為3。這一節用丙酮的里德堡激發態為例，介紹下怎么指認里德堡激發。

這里是在B3LYP/aug-cc-pVTZ下做的TDDFT計算，共算了10個態。注意如前文所述，B3LYP不足以給出合理的里德堡態激發能，用wB97XD會好得多。這里用B3LYP主要是因為發現在wB97XD下計算這些激發態時會有很多軌道對兒躍遷都明顯參與其中，指認起來麻煩，而用B3LYP的話每個激發態都有起主導作用的軌道躍遷，故用作本文例子討論起來比較方便。當然啦，實際研究中總會碰上在計算里德堡態時缺乏主導躍遷的情況，為了指認方便，可以嘗試用NTO方法近似轉化成單一軌道對兒躍遷的形式后再嘗試指認。

此體系第一個激發態在上一節已經討論過，是個價層激發。2~10號激發都是里德堡激發，輸出如下所示
Excited State   2:      Singlet-B2     5.7706 eV 214.85 nm f=0.0281 <S**2>=0.000
      16 -> 18         0.70174

Excited State   3:      Singlet-A1     6.5920 eV 188.08 nm f=0.0025 <S**2>=0.000
      16 -> 19         0.70176

Excited State   4:      Singlet-A2     6.7367 eV 184.04 nm f=0.0000 <S**2>=0.000
      16 -> 17        -0.10656
      16 -> 20         0.69461

Excited State   5:      Singlet-B2     6.8875 eV 180.01 nm f=0.0127 <S**2>=0.000
      16 -> 21         0.69013
      16 -> 22        -0.12647

Excited State   6:      Singlet-B2     7.2194 eV 171.74 nm f=0.0229 <S**2>=0.000
      16 -> 21         0.12895
      16 -> 22         0.68785

Excited State   7:      Singlet-A1     7.3734 eV 168.15 nm f=0.0405 <S**2>=0.000
      16 -> 23         0.70191

Excited State   8:      Singlet-B1     7.4827 eV 165.70 nm f=0.0109 <S**2>=0.000
      16 -> 24         0.70470

Excited State   9:      Singlet-B2     7.9218 eV 156.51 nm f=0.0001 <S**2>=0.000
      16 -> 25         0.70117

Excited State 10:      Singlet-A2     8.1019 eV 153.03 nm f=0.0000 <S**2>=0.000
      16 -> 26         0.69714

可見電子都是從MO16躍遷走的，前面已提到，這是氧的孤對電子軌道。

由于里德堡軌道分布得十分彌散，主要分布區域離分子主體較遠，涉及的空間范圍很大，但在這些區域內的數值不大，所以考察里德堡軌道特征的時候必須用較小的等值面數值才行。我們先看MO19，如下圖所示，給出了三種不同等值面數值下的圖形。

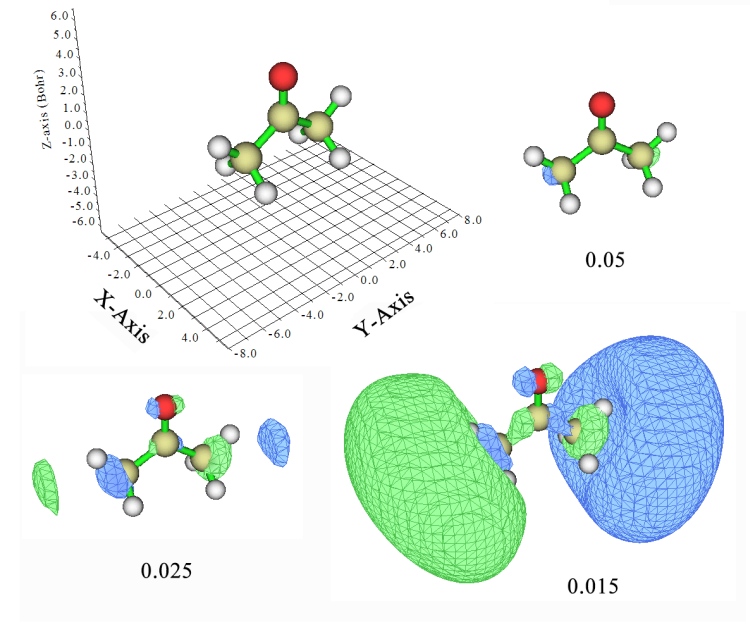
為了明確朝向，坐標軸也在圖中顯示了。這個軌道在Multiwfn默認的等值面數值0.05下看起來非常小，看不出什么特征。將等值面數值降低到0.025后，距離兩端甲基比較遠的地方開始出現了等值面。繼續降低到0.015，兩端的等值面變得相當大了，并且一頭相位為正一頭為負，其整體形狀頗為類似于py原子軌道，因此，這個分子軌道就是py型里德堡軌道。由于此體系的價層軌道都是2s、2p這些主量子數為2的原子軌道構成的，顯然這個彌散的里德堡軌道主量子數應是更高一層的3，因此這個激發應記為n->3py。

我們將計算得到的9個里德堡激發態涉及的所有軌道，即MO18~26號軌道的圖形和對應的原子軌道類型都標注上了。為了清晰起見，有的圖等值面數值為0.015有的為0.01。第4激發態中17號軌道也有參與，但貢獻太小，所以這里忽略了。

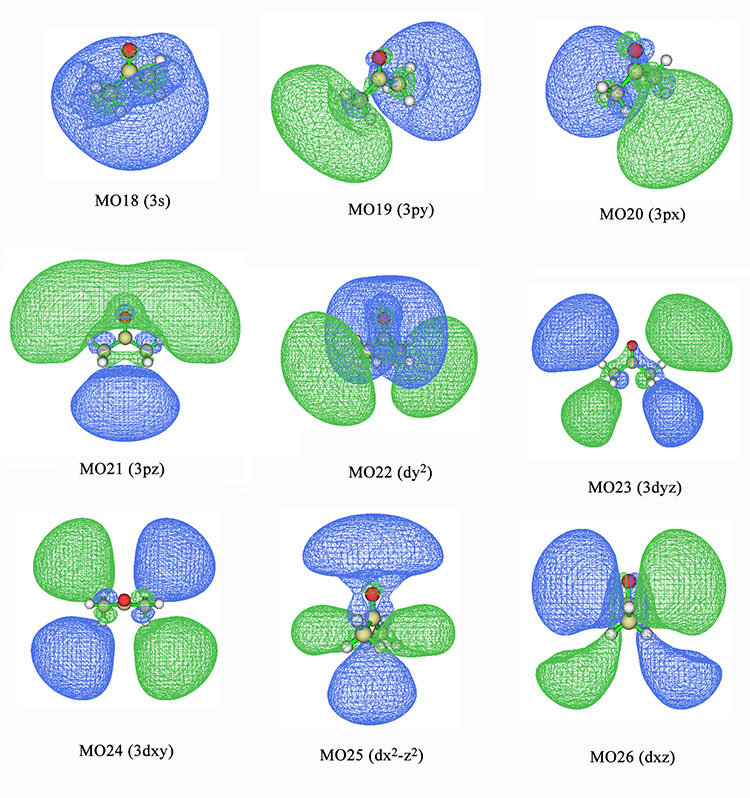
由圖可見，MO18應當被指認為3s軌道，因為等值面整體輪廓呈球狀，和s軌道特征很像。因此，S0->S2激發應當記為n->3s。MO19、MO20、MO21都是整體輪廓顯現出3p軌道特征，即有相位相反的明顯的兩個瓣。MO22~MO26展現的是3d軌道特征。其中MO23~MO26都是有四個瓣，一看就是d軌道的模樣。而MO22看起來不是特別像常見的dz2原子軌道的形狀，畢竟這是個分子沒法要求其軌道看起來和原子軌道十分相似，為了指認它就需要腦洞全開，不要在意細節。從整體輪廓上看將MO22指認成dz2是合理的，因為都是兩端相位相同、中間相位相反這樣的特征。注意圖中標注的軌道的x、y、z符號都是相對于實際計算中的笛卡爾坐標軸而言的（見前面圖中笛卡爾軸和丙酮分子朝向的關系），因此圖中有dx2-z2、dy2這樣的標注。這和通常所用的d原子軌道符號dx2-y2、dz2不符，因此寫到文獻里的時候，應該把圖中的z替換為y，y替換為z。

4 里德堡與價層激發的關系

關于價層激發、價層軌道與里德堡軌道、里德堡激發的關系，在這里再順便多說幾句。

上面討論的軌道最高只涉及到MO26。再往上還會看到其它更高階的里德堡軌道，比如MO27是4s。價層空軌道和里德堡軌道間能量有高有低，誰高誰低不一定。比如上面圖中的里德堡軌道能量高于LUMO（MO17，pi*），但是低于能量較高的sigma*軌道。通常含pi鍵的體系最低的數個空軌道都是pi*。對于沒有pi鍵的體系，LUMO往往就已經是里德堡軌道了，比如水分子、己烷（當然，前提是基組有彌散函數，否則只會看到sigma*）。

相應地，里德堡激發能和價層激發能誰高誰低也不一定。比如電子激發到能量通常較高的sigma*軌道，或者從相對較低階的占據軌道向較低的價層空軌道激發，激發能都會大于很多里德堡激發。所以判斷激發是價層激發還是里德堡激發不是看能量高低，而是看電子激發后分布是否很彌散。對于含pi鍵的體系，里德堡激發通常會高于最低階的價層激發（類型一般為n->pi*、pi->pi*），對于有機大共軛體系一般感興趣的能量范圍內涉及的都是價層激發。對于沒有pi電子的體系，最低的激發常常就已經是里德堡激發了。

前面提到過必須用帶有充足的彌散函數的基組才能合理描述里德堡態。為說明這一點，這里用B3LYP結合不帶彌散函數的TZVP計算丙酮，結果如下

Excited State   1:      Singlet-A2     4.4553 eV 278.29 nm f=0.0000 <S**2>=0.000
      16 -> 17         0.70494

Excited State   2:      Singlet-B2     6.6967 eV 185.14 nm f=0.0272 <S**2>=0.000
      16 -> 18         0.70586

Excited State   3:      Singlet-A1     8.2111 eV 151.00 nm f=0.0010 <S**2>=0.000
      15 -> 17         0.26041
      16 -> 19         0.65464

Excited State   4:      Singlet-A2     8.4564 eV 146.62 nm f=0.0000 <S**2>=0.000
      14 -> 17         0.70152

第一個激發態和aug-cc-pVTZ下計算的時候一樣是n->pi*價層激發。aug-cc-pVTZ下激發能是4.4326eV，和這里4.4553eV基本一致，說明彌散函數并不怎么影響價層激發的激發能。第二個激發和aug-cc-pVTZ的時候一樣也是16->18，雖然TZVP不含彌散函數，但最外層基函數是半彌散的，從MO18的軌道圖上看依然能看出是3s特征。然而，由于彌散函數的缺失，TZVP下終究沒法完全充分地展現MO18的彌散特征，導致激發能6.6967eV比aug-cc-pVTZ的時候5.7706eV高出不少，所以沒有充足的彌散函數就不可能準確計算出里德堡激發態的能量。當前第三激發態也是里德堡態，其激發能8.2111eV也比aug-cc-pVTZ下6.5920eV高出很多。當前第四激發態與aug-cc-pVTZ的時候完全不一樣，aug-cc-pVTZ時第四激發態是里德堡態，而現在卻是14->17主導的價層激發，類型為sigma->pi*，其激發能高達8.4564eV是由于電子是從作為HOMO-2的MO14激發上來的。這個例子明確說明，如果沒有彌散函數的話，價層激發和里德堡激發的能量順序會發生變化，里德堡激發能量上升，這也使得在有限的計算的態數下會出現更多的價層激發。價層激發用不用彌散函數無所謂，對激發能計算精度影響不大，也因此，如果只想研究價層激發而忽略里德堡激發，那么可以故意使用沒有彌散函數的基組來很大程度減少里德堡激發態的出現。