談談第一超極化率(beta)的符號的物理意義
談談第一超極化率(beta)的符號的物理意義
文/Sobereve@北京科音 2021-Oct-22
1 前言
在《理論設計由18碳環與鋰原子構成的電場可控的光學開關》(http://www.shanxitv.org/630)里介紹的筆者的Carbon, 187, 78 (2022) DOI: 10.1016/j.carbon.2021.11.005一文里,體系的兩種構型對應的第一超極化率(first hyperpolarizability,β)的某個分量的正負號是相反的,審稿人讓解釋一下原因。可能不少理論研究分子的非線性光學性質的人都沒太留意β符號的物理意義問題,被問及時不知道怎么解釋正負號的不同,我覺得值得專門寫一篇小文談談怎么理解beta的正負號所體現的物理本質。本文將以NaCl為例從多個角度去討論,本文只討論靜態(超)極化率的情況。
2 β的符號的意義
極化率(α)和第一超極化率(β)張量的定義如下
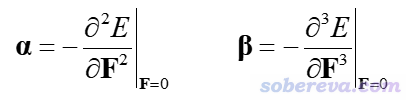
對比可知,對某個分量,如x方向,有以下關系
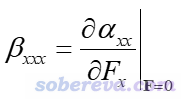
即曰,沖著X正方向施加外電場時如果會導致αxx增大,則βxxx為正,如果導致αxx減小,則βxxx為負。依據這個簡單的道理,我們可以從施加的外電場如何影響極化率的角度去討論超極化率的符號,極化率比起超極化率這個相對抽象的概念要好理解得多。
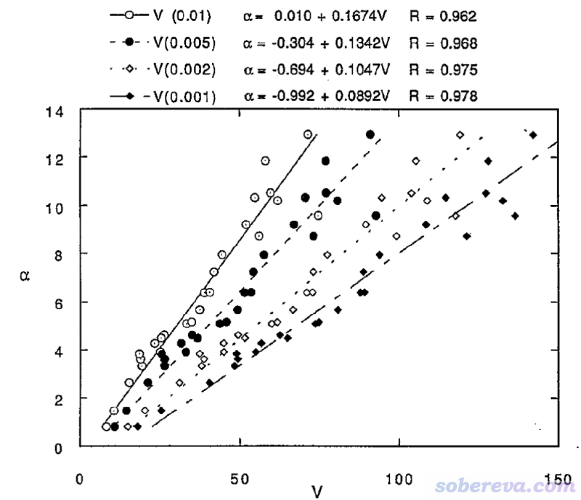
由電子密度等值面包圍區域定義的分子的體積和極化率有密切正相關性,而且對不同類型分子之間對比也是基本適用的,見J. Chem. Phys., 98, 4305 (1993)給出的下圖。這是25種種類各異的分子的分子體積V與實驗極化率的關系,括號里是定義分子體積用的電子密度等值面數值?
在《全面揭示各種尺寸的碳單環體系的獨特的光學性質》(http://www.shanxitv.org/608)里介紹的筆者發表的Chem. Asian J., 16, 2267 (2021) DOI: 10.1002/asia.202100589里,以及討論18碳環合成的前驅體C18-(CO)n的非線性光學性質研究的ChemRxiv (2021) DOI: 10.33774/chemrxiv-2021-mkfdj里,也都有分子體積與極化率的關系的詳細討論,歡迎閱讀,也非常歡迎引用。
順帶一提,也正是基于極化率和體積的密切正相關性,有人提出了分子體系中原子極化率的計算方法,見《使用Multiwfn計算分子中的原子極化率》(http://www.shanxitv.org/600)。
由于上述關系,我們也可以把βxxx的符號是正是負歸結于在X正方向加電場的時候分子體積是增加還是減小上,這把問題轉化為了電場如何影響體系的電子結構層面上。這樣,就可以通過在電子結構分析方面非常強大的Multiwfn程序詳細分析討論了。
3 分析實例:NaCl
這里以一個簡單體系NaCl為例,說明怎么從它的各方面特征受外電場影響的角度理解它的第一超極化率符號的意義。分析用到的Multiwfn程序可以在主頁http://www.shanxitv.org/multiwfn免費下載,本文用的是官網上的最新版。不了解此程序者請參看《Multiwfn入門tips》(http://www.shanxitv.org/167)和《Multiwfn FAQ》(http://www.shanxitv.org/452)。量子化學計算用的是Gaussian 16程序。相關的Gaussian輸入、輸出文件以及由chk轉化出的fch文件都可以在http://www.shanxitv.org/attach/622/file.rar里下載。
此例用的NaCl的結構如下,在B3LYP/def2-TZVP下優化過
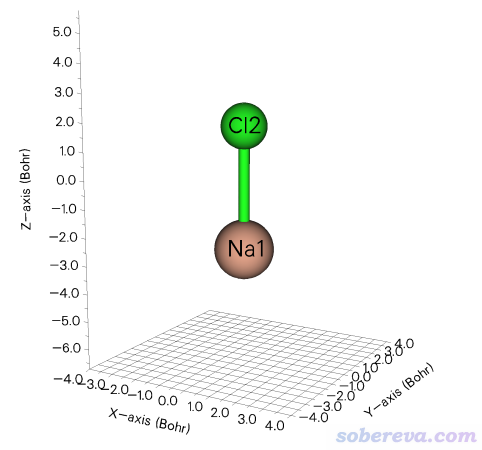
此例對它在B3LYP/aug-cc-pVTZ級別下,向Z正方向加0.01 a.u.電場、不加電場、向Z負方向加0.01 a.u.電場的情況分別做計算,輸入文件分別是本文文件包里的NaCl_z-100.gjf、NaCl.gjf、NaCl_z+100.gjf。注意Gaussian的field關鍵詞設置的電場的方向和習俗相反,這一點在《一篇文章深入揭示外電場對18碳環的超強調控作用》(http://www.shanxitv.org/570)介紹的ChemPhysChem, 22, 386 (2021)文章末尾的computational details部分也專門提過。每個輸入文件里都有polar關鍵詞,目的是獲得不同情況下的分子極化率,參見《使用Multiwfn分析Gaussian的極化率、超極化率的輸出》(http://www.shanxitv.org/231)。nosymm關鍵詞避免Gaussian可能對結構自動做的旋轉,從而確保電場加的方向和期望的一致,見《談談Gaussian中的對稱性與nosymm關鍵詞的使用》(http://www.shanxitv.org/297)。
對不同情況,計算的不同的量如下表所示。Fz=-0.01是沖著Z軸負方向加電場,也相當于從Cl向Na方向加電場;Fz=0.01是沖著Z軸正方向加電場,也相當于從Na向Cl方向加電場。Dipole是電偶極矩,從負電中心指向正電中心。V_vdW是電子密度0.001 a.u.包圍區域的體積,即Bader定義的氣相范德華體積,計算方法見《談談分子體積的計算》(http://www.shanxitv.org/102)。eff. V(Na)和eff. V(Cl)是Na和Cl的有效原子體積,介紹和計算方法見《使用Multiwfn計算分子中的原子極化率》(http://www.shanxitv.org/600)。q_ADCH是筆者在DOI: 10.1142/S0219633612500113提出的ADCH方法算的原子電荷,是很好的原子電荷計算方法(對比見http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml),可以精確重現偶極矩,計算過程例子見Multiwfn手冊4.7.2節。
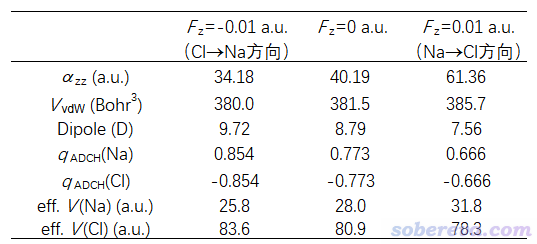
由表中數據可見,沖著Z軸正方向加0.01 a.u.電場后,導致Z方向極化率分量αzz相對于無電場時顯著增加,而沖著Z軸負方向加電場則導致Z方向極化率減小。根據第2節的討論,這對應βzzz為正的情況。確實,無電場時靠polar關鍵詞計算出來的此體系的βzzz=1019.9 a.u.是個明顯的正值。
從上表中的范德華體積可見,從Na向Cl方向加電場后導致范德華體積增加,而Cl向Na方向加電場則導致范德華體積減小。這個變化趨勢和αzz相一致,這和第2節提到的體積和極化率的相關性完全相符,體現了在電子數不變的情況下,若電子密度分布得越廣(對應越大的范德華體積),則體系中的電子對外電場的響應會越顯著。
為什么從Na向Cl方向加電場會使得電子分布得更廣、極化率變大,而反方向加電場則起到相反效果?這可以從這個體系的電子結構來解釋。如上表中無電場時的原子電荷和偶極矩所體現的,Na原子的大部分價電子都轉移到了Cl上,顯著的電子轉移導致了體系很大的偶極矩。Na原子的核電荷在第三周期里是最小的,對其價電子束縛得很弱,這體現在其范德華半徑很大、電離能很低,而且原子的極化率很大(162.7 a.u.)上。而與Na同周期的Cl原子的核電荷相對大得多,它的范德華半徑較小、電離能較高,而且原子的極化率很小(14.6 a.u.)。因此,如果外加電場能誘導Cl上的電子往Na上轉移,就理應導致分子整體的范德華體積增大、極化率增加。從上表中可見,Na向Cl方向加電場時,體系偶極矩減小、Na的原子電荷減小(帶的電子增加),說明電場確實誘導電子分布從Cl向Na方向極化。而電場以相反方向加的時候效果則相反,會令Cl從Na上奪走的電子更多、偶極矩變得更大,也進而令范德華體積和極化率更小。
上面表格里還給出了Na和Cl的所謂的有效原子體積,這由分子中的原子周圍電子密度分布情況所決定。可見,當電場誘導Na上的電子比無電場時增多時,Na的有效體積明顯增加,根據《使用Multiwfn計算分子中的原子極化率》(http://www.shanxitv.org/600)所述這也體現出Na對分子的極化率的貢獻量有顯著的增大。反之,當電場誘導Na上的電子更多地向Cl轉移時,Na的有效體積明顯減小,對NaCl的整體極化率的貢獻也明顯下降。
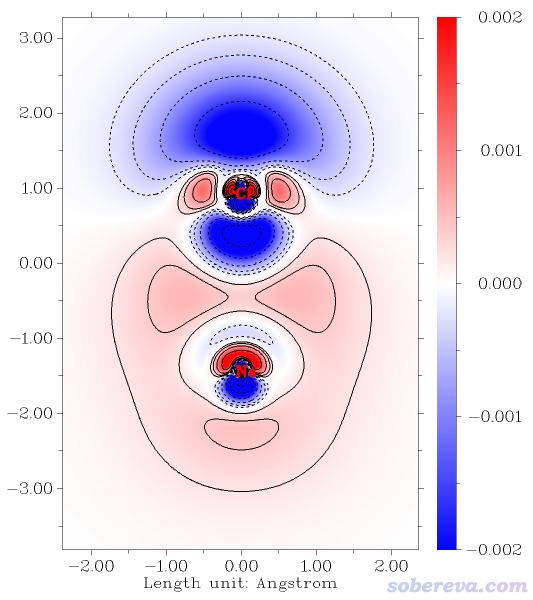
最后,對NaCl繪制穿越鍵軸的截面圖,直觀地看一下電場是怎么影響電子分布的。按照《使用Multiwfn作電子密度差圖》(http://www.shanxitv.org/113)以及Multiwfn手冊4.4節繪制各種風格的平面圖的例子中的步驟,下面繪制了Na向Cl方向加電場時的電子密度與不加電場時的電子密度間的密度差平面圖,紅色、實線部分代表電場導致密度增加區域,藍色、虛線對應密度減小區域。由圖可以清楚地看出電場導致Cl的軸線末端的一片電子以及沖著Na方向的一塊電子整體向Na方向移動并主要分散在Na的價層的一大片區域。
前面提到過Na向Cl方向加電場會導致范德華體積有所增加。為了較直觀地展現這一點,下面給出了Multiwfn的主功能4基于NaCl.fch繪制的無電場時的電子密度等值線圖(繪制方法看Multiwfn手冊4.4節的例子),藍色粗線對應于范德華表面。紅線是從Na向Cl方向加電場時的范德華表面輪廓(先用Multiwfn對NaCl_z-100.fch繪制等值線圖,然后通過ps將其范德華表面對應的粗線疊加到NaCl.fch的圖上)。由圖可見,在圖上方Cl原子末端部分,范德華表面有所收縮,體現出Cl原子半徑減小;而在Na附近范德華表面則有明顯膨脹,而且膨脹程度比Cl那邊收縮的程度更高,這既體現出整個分子范德華體積的增大,也同時體現出Na帶的電子數增加、有效原子半徑增加。

4 總結
本文從電場下分子極化率、范德華體積、電子結構各方面變化的角度充分解釋了第一超極化率符號的內在含義,其中充分利用了Multiwfn程序的相關分析和繪圖功能。本文的分析手段將相對抽象的第一超極化率與物理意義清晰、更易于考察的各種量相關聯使之變得容易理解,這種分析角度值得大家舉一反三討論其它問題。