使用Multiwfn計算分子中的原子極化率
使用Multiwfn計算分子中的原子極化率
文/Sobereva@北京科音
First release: 2021-Jun-4 Last update: 2023-Jul-4
1 前言
原子在孤立狀態下的極化率是可以實驗測量的,也很容易理論計算,在http://ctcp.massey.ac.nz/index.php?menu=dipole&page=dipole有全周期表各種元素的實驗和高精度理論計算數據。分子的極化率可以視為是其中各個原子的有效(effective)極化率的總和(后文簡稱為“原子極化率”),但是分子環境中原子極化率通常不是實驗可觀測的(除非是所有原子等價,比如C60,就用分子極化率除以60就是各個碳的極化率),而且也沒有唯一方式計算,畢竟光是定義分子中原子的空間的方法目前就得有不下20種。
本文將介紹Multiwfn支持的一種計算原子極化率的方法,使用簡便,結果定性合理,對在實際研究中討論哪些原子對分子的極化率起主要貢獻這種問題非常有幫助。
2 原理
在目前已經不怎么流行的Tkatchenko-Scheffler (TS)色散校正方法原文Phys. Rev. Lett., 102, 073005 (2009)中,作者提出了一種簡單的計算分子中原子的靜態極化率αeff(0)的做法。他們的想法很簡單,認為原子的極化率正比于原子體積,因此如果已知孤立狀態原子的極化率αfree(0),那么根據分子環境中原子的有效體積V_eff和孤立狀態下原子體積V_free的比值就可以估計出αeff(0)。在Chem. Rev., 117, 4714 (2017)一文中,這種做法被明確表達為
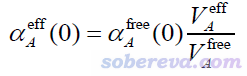
其中A原子的有效體積和自由狀態體積以下面的方式計算。其中r是三維空間坐標,R是原子核坐標,ρ是分子的電子密度,ρ_free是原子在孤立狀態下的密度
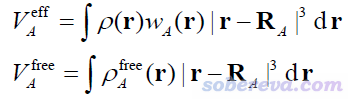
ρ_free可以寫為ρ與原子權重函數的乘積,原文用的是Hirshfeld權重函數(定義可以看《原子電荷計算方法的對比》http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml的2.5節),但也可以用其它的,比如Becke、Hirshfeld-I等。
值得一提的是,以這種方式計算出原子極化率后,還可以計算原子間色散系數C6,這被用于TS色散校正方法中。但這不是本文的范疇,就不多說了。
從2021-Jun-4更新的Multiwfn開始,已經在模糊空間分析(主功能15)中支持了上面介紹的TS方法計算原子極化率的功能。筆者同時還定義了原子對分子極化率的貢獻百分比α%,表達式如下。通過這個量可以非常直觀地了解分子極化率的主要來源。
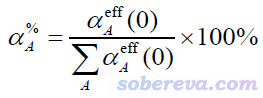
3 實例:噻吩
這里以一個簡單分子噻吩為例演示怎么用Multiwfn計算其中各個原子的極化率。Multiwfn用的是官網上最新版本,可以在http://www.shanxitv.org/multiwfn免費下載。不了解Multiwfn者建議參看《Multiwfn入門tips》(http://www.shanxitv.org/167)和《Multiwfn FAQ》(http://www.shanxitv.org/452)。此例涉及的各種文件都可以在http://www.shanxitv.org/attach/600/file.rar里下載。
使用Multiwfn算原子極化率需要準備分子的波函數文件,以及其中各個元素的波函數文件,后者用來計算前文式子中的ρ_free。可以使用任意量子化學程序計算Multiwfn支持的任意波函數文件格式,比如可以用Gaussian計算wfn、wfx、fch文件,也可以比如用ORCA計算molden文件,等等。參看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。這里我們就用Gaussian計算fch文件。
先對噻吩進行優化(這里順帶做了振動分析,非必需),輸入文件如下。就用中等的計算級別比如B3LYP/def-TZVP就夠了。
%chk=C:\gtest\thiophene.chk
# B3LYP/TZVP opt freq
[空行]
Title Card Required
[空行]
0 1
C 0.00000000 -1.22130969 -0.02179399
C 0.00000000 -0.71608155 1.25941477
C -0.00000000 0.71608155 1.25941477
C -0.00000000 1.22130969 -0.02179399
S 0.00000000 0.00000000 -1.16395234
H 0.00000000 -2.27646271 -0.28794720
H 0.00000000 -1.31244733 2.17357142
H -0.00000000 1.31244733 2.17357142
H -0.00000000 2.27646271 -0.28794720
算完后把thiophene.chk用formchk轉換成fch。然后對其中包含的元素C、H、S原子分別做單點計算得到fch文件。比如C的輸入文件如下。注意C、S基態都是三重態。
%chk=C:\gtest\C.chk
# B3LYP/TZVP
[空行]
Title Card Required
[空行]
0 3
C
三種原子都這么算完后,我們就有了C.fch、H.fch和S.fch。
現在啟動Multiwfn,輸入thiophene.fch的路徑載入之,然后輸入
15 //模糊空間分析
-1 //修改原子空間定義方式
3 //從原先默認的Becke切換為TS方法原文用的Hirshfeld劃分
13 //計算原子有效體積、自由體積和極化率
H.fch //H的孤立狀態的波函數文件的路徑
C.fch //C的孤立狀態的波函數文件的路徑
S.fch //S的孤立狀態的波函數文件的路徑
一眨眼就算完了,輸出信息如下
Atom 1(C ) Effective V: 37.432 Free V: 34.930 a.u. Ratio: 1.072
Atom 2(C ) Effective V: 35.007 Free V: 34.930 a.u. Ratio: 1.002
Atom 3(C ) Effective V: 35.007 Free V: 34.930 a.u. Ratio: 1.002
Atom 4(C ) Effective V: 37.432 Free V: 34.930 a.u. Ratio: 1.072
Atom 5(S ) Effective V: 60.815 Free V: 74.333 a.u. Ratio: 0.818
Atom 6(H ) Effective V: 5.592 Free V: 7.888 a.u. Ratio: 0.709
Atom 7(H ) Effective V: 5.219 Free V: 7.888 a.u. Ratio: 0.662
Atom 8(H ) Effective V: 5.219 Free V: 7.888 a.u. Ratio: 0.662
Atom 9(H ) Effective V: 5.592 Free V: 7.888 a.u. Ratio: 0.709
Calculation took up 0 seconds wall clock time
Atomic polarizabilities estimated using Tkatchenko-Scheffler method:
1(C ): 12.109 a.u. Contribution: 16.13 % (Ref. data: 11.300 a.u.)
2(C ): 11.325 a.u. Contribution: 15.08 % (Ref. data: 11.300 a.u.)
3(C ): 11.325 a.u. Contribution: 15.08 % (Ref. data: 11.300 a.u.)
4(C ): 12.109 a.u. Contribution: 16.13 % (Ref. data: 11.300 a.u.)
5(S ): 15.872 a.u. Contribution: 21.14 % (Ref. data: 19.400 a.u.)
6(H ): 3.195 a.u. Contribution: 4.25 % (Ref. data: 4.507 a.u.)
7(H ): 2.982 a.u. Contribution: 3.97 % (Ref. data: 4.507 a.u.)
8(H ): 2.982 a.u. Contribution: 3.97 % (Ref. data: 4.507 a.u.)
9(H ): 3.195 a.u. Contribution: 4.25 % (Ref. data: 4.507 a.u.)
Sum of atomic polarizabilities: 75.094 a.u.
可見程序先輸出了有效體積和自由體積,并且把二者的比值輸出了。S和H的Ratio都小于1,說明它們在噻吩中的有效體積相比于孤立狀態都有所降低,而降低的程度各有不同。接下來程序根據TS方法算出了原子極化率,比如S是15.872 a.u.,這就相當于其Ratio值0.818與硫在孤立狀態下的極化率19.4(Ref. data后面顯示的,即前文說的αfree(0))的乘積。各種元素的αfree(0)是Multiwfn內置的,是http://ctcp.massey.ac.nz/index.php?menu=dipole&page=dipole里的表格中的推薦值,一直到120號元素都有。Contribution后面給出的值是前文說的α%,即此原子的極化率占所有原子極化率加和的百分比,明確體現了原子貢獻程度。從單個原子貢獻來看,硫原子對噻吩的極化率的貢獻最大,其次是碳原子,貢獻最小的是氫原子。
最后程序給出的75.094 a.u.是所有原子極化率的加和。如果計算原子極化率的方法完美,這個值應當恰好等于分子的實驗極化率或者高精度方法計算的結果。但TS方法畢竟不嚴格,而且受原子空間劃分方式選取的影響大,所以也不要指望這么算出的原子極化率的加和能與分子極化率太相符。如果你不熟悉分子極化率的計算的話,參看《使用Multiwfn分析Gaussian的極化率、超極化率的輸出》(http://www.shanxitv.org/231),筆者用PBE0/aug-cc-pVTZ級別算了下當前這個體系的(各項同性)分子極化率,結果是64.0 a.u.。雖然原子極化率的加和與這個值有一定差異,定量討論原子貢獻的絕對值有些牽強,但只是根據α%討論原子貢獻相對的大小的話,是完全沒問題的。
Multiwfn里也可以基于Becke或Hirshfeld-I劃分計算原子極化率,就是在選擇劃分方式的界面里選擇相應選項,然后照常用選項13計算即可。大家會發現不同劃分下得到的原子極化率的結果是有一定差異的,對于體系中有離子性很強的原子,在原理上用Hirshfeld-I更好一些,因為從方法允許原子空間自洽地調整,但需要花費更多的耗時。
比如這里再用Hirshfeld-I方法算一下,輸入
-1 //修改原子空間定義方式
4 //Hirshfeld-I劃分
1 //開始構造Hirshfeld-I權重函數
13 //計算原子有效體積、自由體積和極化率
由于我們上次計算的時候已經輸入過H.fch、C.fch和S.fch的路徑了,所以這次程序就不要求你重新輸入一遍了。這次的結果為
Atomic polarizabilities estimated using Tkatchenko-Scheffler method:
1(C ): 12.625 a.u. Contribution: 17.05 % (Ref. data: 11.300 a.u.)
2(C ): 10.597 a.u. Contribution: 14.31 % (Ref. data: 11.300 a.u.)
3(C ): 10.597 a.u. Contribution: 14.31 % (Ref. data: 11.300 a.u.)
4(C ): 12.625 a.u. Contribution: 17.05 % (Ref. data: 11.300 a.u.)
5(S ): 16.755 a.u. Contribution: 22.62 % (Ref. data: 19.400 a.u.)
6(H ): 2.693 a.u. Contribution: 3.64 % (Ref. data: 4.507 a.u.)
7(H ): 2.741 a.u. Contribution: 3.70 % (Ref. data: 4.507 a.u.)
8(H ): 2.741 a.u. Contribution: 3.70 % (Ref. data: 4.507 a.u.)
9(H ): 2.693 a.u. Contribution: 3.64 % (Ref. data: 4.507 a.u.)
Sum of atomic polarizabilities: 74.069 a.u.
可見和之前的Hirshfeld劃分時的結果相仿佛。讀者也可以嘗試用Becke劃分再算一次。根據筆者的簡單測試,Hirshfeld劃分得到的原子極化率的加和傾向于高估分子極化率,而Becke劃分時則傾向于低估。
最后,值得一提的是大家可以把原子對極化率的貢獻通過原子著色方式直觀地展現,便于讀者一目了然地看出哪些原子貢獻較大。參考《使用Multiwfn+VMD以原子著色方式表現原子電荷、自旋布居、電荷轉移、簡縮福井函數》(http://www.shanxitv.org/425)里的做法舉一反三即可。