談談有小虛頻時熱力學量的計算
談談有小虛頻時熱力學量的計算
文/Sobereva@北京科音 2024-Feb-9
0 前言
量子化學研究中在優化完極小點結構然后做振動分析時遇到虛頻是家常便飯的煩人的問題。之前我專門寫過博文《Gaussian中幾何優化收斂后Freq時出現NO或虛頻的原因和解決方法》(http://www.shanxitv.org/278)講了怎么消虛頻。除非程序存在bug,否則原理上不存在按上文處理完全解決不掉的虛頻。一個現實問題是:雖然靠各種嘗試、折騰,最終確實總能消掉虛頻,但這個過程對于大體系來說過于浪費計算時間,也耗費研究者的精力。那么是否帶有虛頻的結構就一定不能拿來算能量相關的問題呢?是否虛頻總是要不惜一切代價消除呢?此文就談談我個人的看法,給出理論分析,并且通過一個例子對我的觀點予以驗證。
本文牽扯到熱力學數據計算的各種常識知識,沒有這些常識的話先看《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552),以及Shermo程序手冊的附錄,里面有計算原理的簡潔易懂的概述。在北京科音基礎(中級)量子化學培訓班(http://www.keinsci.com/workshop/KBQC_content.html)里對熱力學量的計算有非常全面深入的介紹,歡迎關注和參加。
本文說的小虛頻和過渡態必然存在的虛頻沒有絲毫聯系,初學者絕對不要把本文內容胡亂套用到過渡態的情況。
1 導致小虛頻的原因
為了避免誤解,首先回顧一下優化極小點后振動分析時出現虛頻的各種常見原因:
(1)振動分析時用的影響勢能面的設置與優化時的不同。這通常是沒有基本常識的外行人才會犯的低級錯誤。注:JCTC, 17, 1701 (2021)中提出的single-point Hessian (SPH)方法通過對勢能面添加偏移勢,從而允許振動分析用的計算級別低于優化用的級別來節約時間,但這個做法非主流、經驗性強,本文不涉及
(2)初始結構的點群高于實際極小點的點群,且如果優化后的結構維持住了初始的對稱性,振動分析后就會發現破壞對稱性的虛頻,即按照虛頻方式移動結構會導致結構的對稱性下降。有時候這種有虛頻的結構恰對應于過渡態
(3)程序bug。比如Gaussian 09 D.01的DFT-D3色散校正對解析Hessian的貢獻的計算有bug,容易導致算勢能面平緩體系出現虛頻。這點在《DFT-D色散校正的使用》(http://www.shanxitv.org/210)我專門做了說明
(4)某些方法對勢能面引入明顯數值噪音。如Gaussian中的SMD溶劑模型的這個問題就比較明顯
(5)幾何優化收斂得不精確。幾何優化收斂限過于寬松或Hessian的質量不太好會導致這種問題。
(6)積分格點質量不夠好。這個問題對于M06-2X等對積分格點敏感的泛函尤為顯著。關于量子化學程序用的原子中心的積分格點參考《密度泛函計算中的格點積分方法》(http://www.shanxitv.org/69)。如果是CP2K等利用平面波的第一性原理程序,用的均勻分布的格點依賴于平面波截斷能的設置。
以上前四種情況導致的虛頻是一定要解決掉的,而且本來解決就非常簡單。只要不犯低級錯誤自然就沒有(1)的情況出現,解決(2)按照虛頻模式調節結構后進一步優化即可,解決(3)就換成沒bug的版本或其它計算程序,解決(4)可以換成其它的能在優化+振動分析中實現基本相同目的而沒嚴重數值噪音的方法,如SMD換成IEFPCM,或者用SMD時結合SAS方式定義溶質孔洞表面。對于(5)和(6)情況帶來的虛頻,只要計算能力和精力允許,能消盡量要消,但如果由于計算資源或精力所限實在太難消掉、被迫要容忍虛頻的存在,那么后續的能量相關問題的計算就是后文討論的內容了。
對于柔性大分子、弱相互作用復合物這樣勢能面的某些維度非常平緩的體系,在做完幾何優化和振動分析后很容易發現存在大小非常小的虛頻,如波數為9.8i、27.3i cm^-1這種,普遍小于50,這一般是前述(5)或(6)情況所導致的。此類虛頻的振動模式通常對應于甲基旋轉運動、柔性骨架的變形運動、分子間相對運動。這類(5)或(6)情況所導致的虛頻以下簡稱為“小虛頻”。但要注意也不是所有波數小于50的虛頻都屬于這種情況,前述的其它四種情況也完全可能導致數值很小的虛頻,所以絕對別光拿虛頻大小來判斷情況。
2 有小虛頻時能量相關問題的計算
當遇到小虛頻時,顯然最完美的做法(具體選擇視情況而定)是用諸如更嚴格的幾何優化收斂限、更好的Hessian、更好的積分格點精度進一步做優化和振動分析,使得虛頻完全消除后再計算能量相關問題。但是對于普通泛函算幾百個原子有機體系,很可能算一次Hessian就要花一整天時間,幾何優化一步也可能花費一個小時左右,最終把虛頻完全消掉可能得花幾天甚至一個禮拜,十分痛苦,甚至不可能實現。那么,在后續算能量相關問題時怎么考慮?下面根據被計算的量專門討論。
2.1 計算電子能量
諸如Gaussian這樣的主流量子化學程序默認的幾何優化收斂限是以受力和位移作為判據的。在默認收斂限下優化正常完成后,即便結構還沒有與實際極小點特別精確一致,但通常相差很小。而且當前的最大和平均受力肯定已經很小了(因為收斂限考慮了它們),由于受力對應于能量梯度的負矢量,所以當前結構稍微再挪一點達到精確的極小點的過程中能量變化肯定非常小。即曰,在有小虛頻的情況下,計算的電子能量一般是可以用的,也即結果和消掉虛頻后再算的能量相差極小。
2.2 計算0 K下的內能U(0)
U(0)是電子能量與零點振動能(ZPE)之和。在諧振近似模型下,每個振動模式對ZPE的貢獻是1/2*h*ν,h是普朗克常數,ν是振動頻率。頻率很低的振動模式對ZPE的貢獻是非常小的,每波數的振動頻率對ZPE的貢獻僅為5.98 J/mol,因此諸如30波數的振動模式只對ZPE有0.18 kJ/mol(0.04 kcal/mol)的貢獻,數量級遠遠低于理論方法、基組、溶劑模型等因素帶來的誤差。順帶一提,Shermo計算熱力學量的時候如果把settings.ini里的prtvib設為1,每個振動模式對熱力學量的貢獻都會明確輸出。
主流量子化學程序,以及Shermo程序在默認情況下,在計算振動對熱力學量的貢獻時都是不考慮虛頻產生的貢獻的,因此小虛頻對熱力學量的貢獻會被直接忽略掉,這不會對ZPE的計算造成實際問題。因為如果把這個小虛頻消了,從而產生一個實頻,其頻率肯定也是非常低的,對ZPE的貢獻可忽略不計。也就是不管消不消這個虛頻,算出的ZPE都沒多大差別。不過,實際情況遠沒這么簡單,因為在虛頻消掉前后,由于二者所在勢能面的位置的些許不同,或改用不同檔次積分格點導致頻率計算精度的差異,其它的實頻模式也會多多少少受到影響,不過頻率值受影響相對明顯的主要是低頻模式(可能影響幾個甚至10個左右波數,而高頻模式受影響一般小于2波數),它們對ZPE的貢獻恰恰又很小,所以虛頻消掉前后算的ZPE雖然未必差異小到諸如前面說的0.2 kJ/mol左右這種程度,但至少也不會大,比如對柔性大體系頂多也就影響個1-2 kJ/mol。
如上所述,鑒于是否小虛頻對電子能量和ZPE的影響都不太明顯,因此算電子能量和U(0)時一般可以容忍一個或多個小虛頻的存在。
2.3 計算從0 K升溫到當前溫度對內能的影響
研究U(0)沒太大實際意義,畢竟實際化學過程也不可能在0 K發生。計算有限溫度,也就是高于0 K時候的熱力學量,就需要考慮從0 K升溫到當前溫度對內能的改變量,其中振動產生的貢獻下面用Uvib(0→T)表示。首先要知道一點,低頻對Uvib(0→T)的貢獻是明顯高于高頻模式的。這點從下面的J. Phys. Chem., 100, 16502 (1996)的圖1可以明顯看出來,圖中ΔHvib(T)和這里說的Uvib(0→T)是一碼事,圖是對T=298.15K的情況繪制的。

雖然低頻模式的貢獻大,但是由圖中放大的0-100波數的區間可見,在小幾十波數范圍以內,頻率值對Uvib(0→T)的影響雖然不可忽視,但不算多大,都在2.0-2.4 kJ/mol范圍內。這也就是說,由于存在一個小虛頻導致少考慮一個實低頻模式,會給Uvib(0→298.15K)帶來-2.2 kJ/mol左右的誤差,這雖然不算小,但還算可以湊合接受。如前所述消虛頻后還可能會對其它低頻模式產生不可忽視的影響,這對Uvib(0→T)的改變一般也不至于太大。
綜上所述,若帶著小虛頻計算U(T),會造成一定低估。對于有一個小虛頻的情況,低估程度在0.5 kcal/mol左右。如果有多個小虛頻,那還是別計算U(T)了,除非T遠低于常溫,或者結合后文說的把小虛頻當成實頻的做法。
2.4 計算熵、自由能
低頻對熵的貢獻遠大于高頻,而且在很低頻區間內,頻率越低貢獻明顯越大。在包括Gaussian在內,大多數量子化學程序(ORCA除外)計算熱力學量用的是傳統的rigid-rotor harmonic oscillator (RRHO)模型,振動熵的計算完全基于諧振近似模型。此時在低頻區間內,隨著頻率趨近于0,振動模式對熵的貢獻猛增,如下面的Chem. Eur. J., 18, 9955 (2012)文中圖2的虛線所示。Grimme在這篇文章中還提出了一種quasi-RRHO模型(QRRHO,后來也叫modified RRHO、mRRHO),以下稱為QRRHO(Grimme),它將自由轉子和RRHO用的諧振近似模型算的振動熵做插值,頻率越接近0自由轉子的權重越大、頻率越高諧振近似的權重越大,如下圖實線所示。QRRHO(Grimme)對高頻模式算的熵貢獻和RRHO完全一樣,而對于低頻模式(特別是波數在100以下的)考慮得比RRHO明顯更合理。由下圖還可見QRRHO(Grimme)算的低頻模式的熵比RRHO整體小得多,沒有RRHO的嚴重高估的問題。此外,QRRHO(Grimme)下低頻模式的振動熵對頻率值的敏感性低于RRHO很多。

直接計算熵的用處不大,算熵的主要目的是用來算自由能,因為自由能里有-T*S項。顯然低頻對熵的貢獻計算的準確度顯著影響到自由能的計算準確度。假設體系有一個小虛頻,并且在消掉之后會多一個20 cm^-1的實頻,并且用的是QRRHO(Grimme)算298.15 K的熵,那么在有虛頻的結構下由于缺失了這個實頻,根據上圖可知會造成熵的誤差約為-18 J/mol/K,對自由能造成的誤差約為-298.15*(-18)/1000=5.4 kJ/mol,略高于1 kcal/mol,這就不小了,都能趕上高質量ωB97M-V泛函結合大基組算普通有機反應的誤差了。不過實際中小虛頻帶來的誤差未必那么大,因為有和沒有小虛頻的結構下實低頻模式的頻率也往往有不可忽視的不同,例如下面第3節的例子在有虛頻的結構下實低頻模式的頻率比精確極小點結構下的整體偏小(勢能面形狀原因所致),導致高估了不少實低頻模式的熵,藉由-T*S項進而對自由能造成低估,于是和少考慮一個低實頻對自由能的高估產生了很大程度的相互抵消,下面管這稱為“熵的誤差抵消”。
根據以上討論,有小虛頻的情況下計算熵和自由能都有一定風險。如果就有一個小虛頻,算常溫的情況往往還說得過去,而如果有多個小虛頻,或計算高溫的情況(注意T越大-T*S越大,熵的誤差造成自由能的誤差越大),我就不建議冒險帶著虛頻了。而且就算非要帶著小虛頻算,也至少應當用QRRHO模型,而切勿用RRHO模型,因為RRHO算的振動熵對低頻頻率值的敏感程度顯著高于QRRHO,因而用有虛頻的結構算的熵的誤差上限比QRRHO的明顯要大。
要注意QRRHO模型不止Grimme提出的這一種。如Shermo手冊附錄部分所介紹的,Truhlar的QRRHO是把所有小于一定閾值(通常為100 cm^-1,可以由Shermo的ravib參數控制)的低頻統一提升為這個閾值再算它們對Uvib(0→T)和熵的貢獻,這個做法的物理意義不甚明確,沒有QRRHO(Grimme)的插值做法優雅。目前還有一種QRRHO是Minenkov等人在J. Comput. Chem., 44, 1807 (2023)中提出的,它對振動熵部分的考慮和QRRHO(Grimme)一樣,但還同時將這種自由轉子與諧振近似做插值的思想同時應用到了計算振動對內能的熱校正量Ucorr上(此時沒法單獨計算ZPE),原理更理想,實際結果還略好一點點。這些QRRHO模型在最新版Shermo中都是支持的,通過ilowfreq參數控制。
2.5 將小虛頻視為實頻的做法
在Angew. Chem. Int. Ed. 2022, e202205735中的3.2節Grimme等人認為存在小虛頻的情況下,只要使用QRRHO模型并且將小虛頻視為實頻處理,比如18i cm^-1直接當做18 cm^-1,則得到的熵就是可以用的、小虛頻的存在就不再是個問題。這種做法表面看起來似乎有點莫名其妙、太任性了,但確實有一定道理,可以這么理解:在消除小虛頻后,必定會得到相同數目的波數也很小的實頻模式,它們都對熵有明顯貢獻。相對于完全忽略掉這些小虛頻的貢獻而導致明顯低估熵,干脆把他們當做實頻處理,從而“湊”出來相應數目的實低頻是更好的做法,而且本身在QRRHO模型下,數值在十幾、幾十波數區間的頻率對熵的貢獻也都相差不懸殊,因此也用不著對這么人為湊的實頻頻率太較真。由于如前所述,Uvib(0→T)也對低頻數值不敏感而低頻的貢獻又沒小到可以隨便忽略的程度,所以計算Uvib(0→298.15K)時也使用這種處理是有道理的。從Shermo 2.5版開始,可以通過settings.ini里的imagfreq選項設置視為實頻的虛頻閾值,比如設為50,就代表大小在50 cm^-1以內的虛頻都當做實頻處理來計算振動對各種熱力學量的貢獻,此時從Shermo程序輸出的頻率信息中也會看到已經沒有虛頻了。
然而,這種將小虛頻視為實頻的做法目前很非主流,其思想在我來看過于主觀和樂觀、把問題想得太簡單了,目前也缺乏系統性的檢驗,我個人不建議輕易使用。這種做法有一個明顯問題:如前所述,有小虛頻和消掉虛頻的兩種情況相差的不僅僅是一個小虛頻轉變成一個小實頻,許多其它低頻模式的頻率也會有不小變化,而且有時是整體明顯增加的。不做這個虛頻到實頻的轉換的情況下能夠有上一節說的熵的誤差抵消效應,而這么做了之后,忽略虛頻模式導致對熵的低估問題確實很大程度解決了,但在有小虛頻結構下其它頻率往往偏低而導致熵的高估帶來的誤差就沒處抵消了。此外,如果當前體系的低頻還有很多都是10 cm^-1 左右這種特別低的,這個范圍附近即便是QRRHO(Grimme)或QRRHO(Minenkov)模型算的熵也對頻率很敏感,問題會更大。
所以,將小虛頻視為實頻的做法雖然確實對一些情況更好地計算熵和自由能是有幫助的,但也很可能起到負面效果。所以這絕不是普適、穩健、理想的做法,更千萬不能一看到存在小虛頻就總是想靠這個做法來完全無視虛頻。
3 有虛頻時算熱力學量的實例
筆者最近通過Gaussian 16在ωB97XD/6-311G*級別研究的一個以pi-pi堆積方式形成的共128個原子的三分子復合物,在優化和振動分析后發現存在6.44i cm^-1的小虛頻,之后進一步優化時用opt=calcfc關鍵詞提供精確的初始Hessian,優化完再做振動分析就發現沒虛頻了,此時最低的頻率成了10.35 cm^-1。正好這個例子可以拿來考察消虛頻前后計算的熱力學量的差異,由此檢驗帶著那個小虛頻時以不同方式算的熱力學量有多大誤差。要強調的是,僅僅這么一個測試,顯然不足以充分證明某種做法理想,因為這必須通過大量體系做統計分析,但至少誤差較大的情況可以用來體現相應做法不夠穩健和普適。
先看一下有虛頻相對于無虛頻時各個實頻的頻率變化情況。先把實頻頻率按照由低到高排列,用有虛頻時候它們的頻率減去無虛頻時候的頻率作為縱坐標值,而兩種情況頻率的平均值作為橫坐標,作的圖如下所示。可見,至少對于此例,有虛頻時數值較低的實頻是普遍明顯偏低不少的,而>200 cm^-1的相對而言的中、高頻則受到的影響很小。這種情形雖然不能說是普遍情況,但至少也是挺常見的一種。
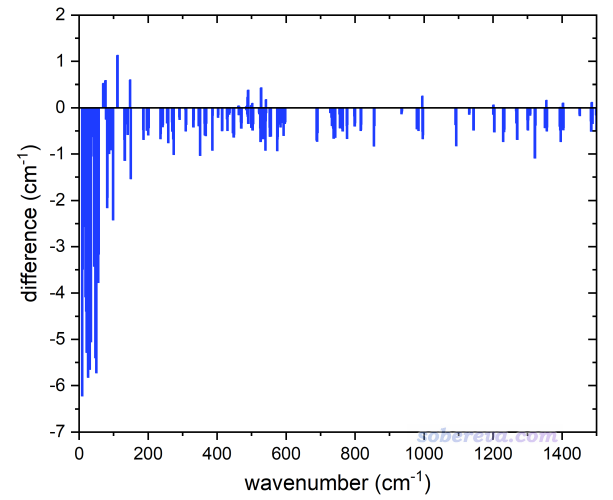
此例有虛頻相對于無虛頻的情況計算的電子能量僅僅相差0.04 kcal/mol,小到完全可以忽略不計。用Shermo程序基于Gaussian振動分析輸出文件計算的有虛頻相對于無虛頻時的ZPE和氣態標況下的熵、內能、自由能熱校正量的差異如以下表格所示。RRHO以及Truhlar、Grimme、Minenkov三種QRRHO分別對應Shermo的ilowfreq=0/1/2/3的情況,imagreal=0和50相當于忽略那個虛頻以及把那個虛頻當大小相同的實頻考慮的情況。

首先看常規的忽略虛頻貢獻的情況。由表格可見:
? ZPE:有虛頻時和無虛頻時ZPE相差僅-0.3 kcal/mol,屬于通常可以接受的差異
? 熵:由于誤差抵消的巧合,恰好RRHO下有小虛頻時的熵和無虛頻時的差異很小。QRRHO(Truhlar)的情況差異挺大,在于它把實低頻都統一當成了100 cm^-1,這部分在有和沒有小虛頻情況之間幾乎都抵消了,而有小虛頻時相當于少考慮了一個100 cm^-1振動模式對熵的貢獻,因此造成熵的嚴重低估。QRRHO(Grimme)和QRRHO(Minenkov)對熵的部分處理相同,由于前述的熵的誤差抵消效應導致有和沒有小虛頻時熵的差異不算太大
? 內能的熱校正量Ucorr:等于ZPE+Uvib(0→T)。由于Uvib(0→T)對低頻的具體數值不太敏感,有無小虛頻情況下實低頻的貢獻變化很小,而有小虛頻時由于缺失了一個低實頻對Uvib(0→T)的貢獻,導致有小虛頻時Uvib(0→T)偏低不少,Ucorr因此比ZPE偏低得明顯更多。QRRHO(Minenkov)用的計算Ucorr的方式和其它模型不同,對于此例使得有小虛頻時Ucorr偏低程度比其它模型更小,僅為-0.5 kcal/mol。因此在計算有小虛頻情況下的U(T)時,用QRRHO(Minenkov)可能會比其它模型更有優勢。
? 自由能的熱校正量Gcorr:相對于其它模型,有小虛頻相對于無虛頻時Gcorr的差異在RRHO下是最大的,這在于有無小虛頻時RRHO算的S的差異對此例恰好頗小,導致-T*S項的差異才0.03 kcal/mol,因此沒能充分對Ucorr的差異產生抵消效應。而各種QRRHO模型下Gcorr的差異明顯較小,這在于這種情況下S的差異不小,而且-T*S項的差異的符號和Ucorr的差異相反,因此相互抵消了很多。其中Gcorr差異最小的是QRRHO(Minenkov),才-0.11 kcal/mol,體現出它可能適合作為有小虛頻情況下算自由能的優先選擇。
再來看將小虛頻當實頻處理的情況。根據以上表格可見,這種處理使得Ucorr在有和沒有小虛頻情況下計算的結果差異減小很多,因此對于算內能的目的,這種做法有一定意義。但是,除了QRRHO(Truhlar)外,這個做法卻造成了有小虛頻時算的S和Gcorr與無虛頻時的差異變得顯著更大,對RRHO最為嚴重,對QRRHO(Grimme)和QRRHO(Minenkov)問題也挺嚴重,這來自于有小虛頻時實頻模式偏低造成的對振動熵的高估無法與因為少考慮一個實低頻導致的低估一定程度相抵消。把小虛頻當實頻處理時結合QRRHO(Truhlar)對此例倒是很不錯,有小虛頻相對于無虛頻時的熵只相差0.27 cal/mol/K,這在于此種QRRHO將低頻全都上拉到100 cm^-1,此時又把小虛頻轉化成了小低頻,因此無虛頻和有虛頻時相當于有同等數目的100 cm^-1的實頻,自然兩種情況下算的熵很接近。
4 總結
根據以上討論和實際體系的測試可知,對于因(5)和(6)情況造成有小虛頻的情況,算電子能量和U(0)沒大問題,不是非得消虛頻。
對于計算Ucorr或與之相差RT的焓的熱校正量Hcorr,用QRRHO(Minenkov)或QRRHO(Grimme)并同時把小虛頻當實頻處理是較好選擇,不會因為存在小虛頻的問題而帶來太大誤差。
有小虛頻時最難搞的是熵,以及溫度不很低時候Gcorr的計算,難點在于小虛頻消掉前后實低頻模式頻率也可能受到不小影響且影響情況不易估計,然而即便用QRRHO(Grimme或Minenkov)時低頻的具體數值對熵的影響也不算太小,所以明顯不是把小虛頻當成實頻處理以避免少考慮一個實低頻模式就能較好解決的,而且如第3節的測試可見,這種做法還可能造成熵和Gcorr在有小虛頻時計算結果更差。所以當你對熵、Gcorr要求精度高時,小虛頻要盡量消。實在搞不定的話,那就姑且用原理上最好的QRRHO(Minenkov),并且建議不用小虛頻當實頻的處理,畢竟此做法非主流而且起到正面效果的可能性很有限。雖然把小虛頻當實頻并結合QRRHO(Truhlar)的情況下小虛頻和無虛頻時熵的差異很小,但在J, Comput. Chem., 44, 1807 (2023)的測試中QRRHO(Truhlar)算團簇反應自由能表現得遠不如QRRHO(Minenkov),甚至比RRHO沒明顯改進,所以我也不推薦。