談談如何計算環張力能:以CPP和碳單環體系為例
談談如何計算環張力能:以CPP和碳單環體系為例
文/Sobereva@北京科音 2024-Jan-29
0 前言
環狀化學體系具有不同程度的環張力,環張力和環狀體系的諸多問題緊密相關,諸如生成焓、穩定性、合成難易程度等。環張力能(strain energy, SE)是衡量環張力大小的最直接的指標,它對應當前環狀結構轉變為假想的沒有環張力的結構過程中能量變化的負值。
北京科音自然科學研究中心(www.keinsci.com)的盧天等人之前受邀發表了一篇專門精確考察碳環(cyclocarbon)體系環張力能的文章,文中對環張力的計算思想有詳細介紹并給出了諸多討論:
Accurate theoretical evaluation of strain energy of all-carboatomic ring (cyclo[2n]carbon), boron nitride ring, and cyclic polyacetylene, Chin. Phys. B, 31, 126101 (2022) DOI: 10.1088/1674-1056/ac873a(不方便獲取者也可以看預印版https://doi.org/10.26434/chemrxiv-2022-v8w9h,內容基本一樣)
下面,將基于此論文中的內容簡要說明環張力能的計算原理并給出具體例子。感興趣的讀者請務必仔細閱讀論文原文以了解更多信息,也推薦以類似方式計算其它體系的環張力能時引用此論文。另外,讀者如果對碳環體系感興趣,很建議查看同作者之前發表的此類體系的各種研究文章和相關博文:http://www.shanxitv.org/carbon_ring.html。
1 同聯反應法
設計同聯(homodesmotic)反應是計算環張力能的很常用方法。這個方法設計一個化學反應,既使得環被打開使得環張力被完全釋放,同時又盡可能不影響原本的成鍵情況,顯然這個反應能的負值就對應了環張力能。
例如,要計算氧雜環丁烷的環張力能,就可以設計以下同聯反應。紅色部分對應具有顯著環張力的氧雜環丁烷,將它插入到甲乙醚所示位置就變成了右邊的產物,顯然此時環張力就被完全釋放掉了。與此同時,反應物和產物的成鍵特征并未發生變化,例如下圖紅字的第一個碳在反應前后始終是sp3雜化狀態、始終連著一個氧原子和一個CH2,因此化學環境變化導致的成鍵特征的極輕微改變對這個反應能的影響可以忽略不計,也即這個反應能幾乎只體現出環張力的釋放。
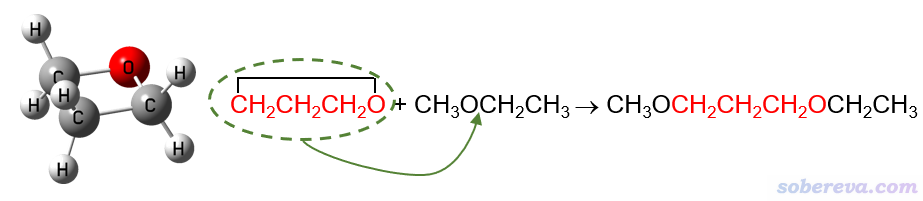
同聯反應法計算環張力能的缺點是反應的設計并不唯一,比如以上反應的甲乙醚也可以是甲醚、乙醚等等,結果或多或少會有點差異。顯然反應應當設計得盡可能令各個鍵的特征在反應過程中不發生改變,但這并非總能很好實現,后文提到的碳環體系就是一例。
2 同聯反應法計算實例:[6]CPP
這一節示例使用同聯反應法計算[6]CPP的環張力能。此體系的幾何結構,以及設計的同聯反應如下所示。可見是把[6]CPP插入到了聯苯中間變成了直線的八聯苯,從而完全釋放了環張力。
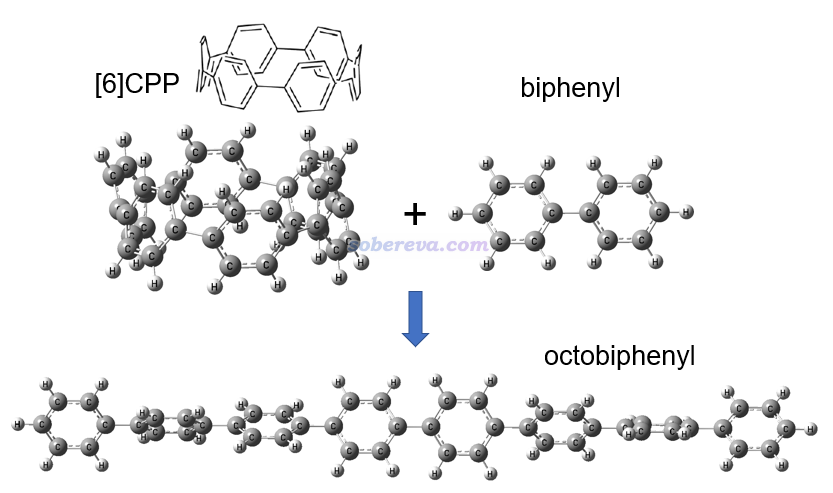
上圖涉及的三個分子都在ωB97XD/6-31G*級別下用Gaussian 16程序進行了幾何優化,并做振動分析確認了無虛頻,輸入輸出文件都在http://www.shanxitv.org/attach/698/file.rar里。基于輸出文件里最后一次輸出的電子能量,用反應物能量之和減去產物能量,就得到了環張力能:627.51*(-463.1444911-1385.7232492+1849.0260518) = 99.3 kcal/mol。這個值比C-C單鍵的鍵能還要大一些,可見其環張力是相當強的。
如果想得到更精確結果,可以基于優化完的結構在更好的級別下算高精度單點再求差,比如基組可以改用明顯更好的def2-TZVP。這對結果可能造成幾kcal/mol程度的影響。
3 外推法
如果被考察的環狀體系是由重復單元構成的,比如前面的[6]CPP是苯環作為重復單元,就也可以用這一節介紹的外推法計算其環張力能。這個方法計算過程如下
(1)計算從小到大不同重復單元數(n)的環的每單元的能量E/n,這里E是整體能量。顯然E/n是依賴于n的,n較小時環尺寸較小,自然環張力大,平均到每個單元的環張力能也大
(2)用Origin之類程序通過恰當的函數(一般是二次函數)擬合E/n與n之間的解析關系,并外推得到n無窮大時的E/n,這對應于沒有環張力時候的每單元能量
(3)將當前考察的環狀體系的E/n減去n無窮大時的E/n,就得到了當前體系的每單元環張力能(SE/n)
(4)將當前體系的SE/n乘以當前的體系的n即是當前體系的環張力能
相較于同聯反應法,外推法的優點:
?原理非常嚴格
?沒有同聯反應法設計反應的任意性,并可以用于同聯反應法不適合的體系
?可以順帶得到環張力能與n的解析關系,由此可以直接預測出任意重復單元數的環張力能
缺點:
?需要計算從小到大不同尺寸的環狀體系,總耗時明顯高于同聯反應法
?計算步驟略繁瑣,得自己做擬合
如果你只是要考察當前一個環狀體系的環張力能,而且可以設計出很合適的同聯反應,那么就沒必要用昂貴且略麻煩的外推法。
4 外推法計算實例:18碳環
2019年首次在凝聚相實驗中觀測到的18碳環分子由18個sp雜化的碳依次相連構成環狀。由于sp雜化的碳明顯傾向于形成180度鍵角,因此18碳環必然有顯著的環張力,具體環張力能是多少非常值得研究,這正是前述Chin. Phys. B, 31, 126101 (2022)文章研究的主要內容。
此文中指出碳環類體系不適合同聯反應法計算環張力能。碳環類體系是長、短C-C鍵交替構成,兩個碳是一個重復單元,若用同聯反應法計算化學式為C_2n的碳環的環張力能,可以設計如下反應式,相當于把碳環的每個重復單元插入到了一定長度的碳炔里。碳炔是sp雜化的碳形成的鏈狀分子,兩端由氫封端。PS:對碳炔感興趣者建議閱讀《氫封端碳鏈H-(C≡C)n-H (n = 3-9, 15)的電子光譜的尺寸依賴性:性質分析及對碳炔的預測》(http://www.shanxitv.org/679)
![]()
然而,如下圖可見,將18碳環的重復單元插入到不同長度(通過m體現)的碳炔里,按照同聯反應算出來的環張力能有明顯區別,因此靠同聯反應法難以得到嚴格的18碳環的環張力能。
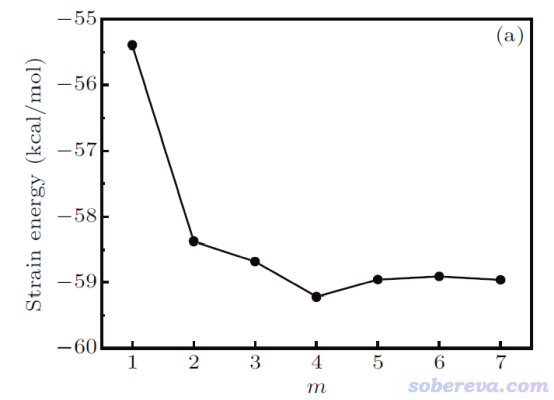
碳炔和18碳環都具有C-C鍵長、短交替的特征。文中還發現,不管碳炔的m取多少,處于它中央的較長的C-C鍵和18碳環中的較長的C-C鍵之間的鍵長差異都不可忽視,對較短的C-C鍵也是如此。因此原理上沒法設計一個同聯反應使得18碳環的C-C鍵特征在轉移到產物時幾乎完全不發生改變,這也必然導致靠同聯反應法不可能對此體系得到完全精確的環張力能,也即成鍵特征差異造成的能量改變會不可避免地摻入到計算出的環張力能中。
由于發現了以上問題,文中使用外推法計算碳環的環張力能。為了追求盡可能好的精度,文中用ORCA程序在精度很好的DLPNO-CCSD(T)/cc-pVTZ級別下對n=7到n=24的碳環都計算了單點能(基于ωB97XD/def2-TZVP優化的結構),ORCA輸出文件在http://www.shanxitv.org/attach/699/file.rar里都提供了。每重復單元能量(E/n)與n的關系如下所示。由于n較小的碳環的電子結構特征有特殊性、和較大的碳環存在一定差異,因此文中只對n>=13的數據點做了二次函數的擬合,由下圖的紅色曲線可見擬合質量超極好,R^2近乎精確為1。
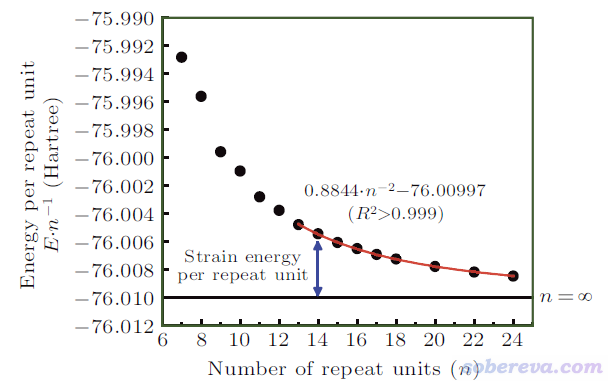
令擬合公式E/n = 0.8844/n^2 - 76.00997中的n為無窮大,就得到了無環張力對應的無窮大的碳環的每單元能量-76.00997 Hartree。每單元環張力能SE/n = E/n - 76.00997,于是有SE/n = 0.8844/n^2,也即碳環類體系的環張力能SE = 0.8844/n Hartree。18碳環的n=9,代進去就得到了其環張力能0.8844/9 Hartree = 61.7 kcal/mol。
值得一提的是,如果令前述同聯反應法中碳炔的m設得很大,從而使得環張力能隨m收斂,最終算出來的結果是59 kcal/mol,可見和嚴格的外推法的結果相比誤差并不可忽略。
前述論文中也測試了用ωB97XD/def2-TZVP的能量結合外推法算碳環的環張力能,結果和上面用的昂貴的DLPNO-CCSD(T)/cc-pVTZ能量的結果沒多大差別。這在一定程度上體現出ωB97XD/def2-TZVP級別算碳環類體系很不錯。
文中還基于不同尺寸碳環的環張力能和鍵角之間的關系,推導出了適合碳環體系用的C-C-C鍵角力常數56.23 kcal/mol/rad^2。
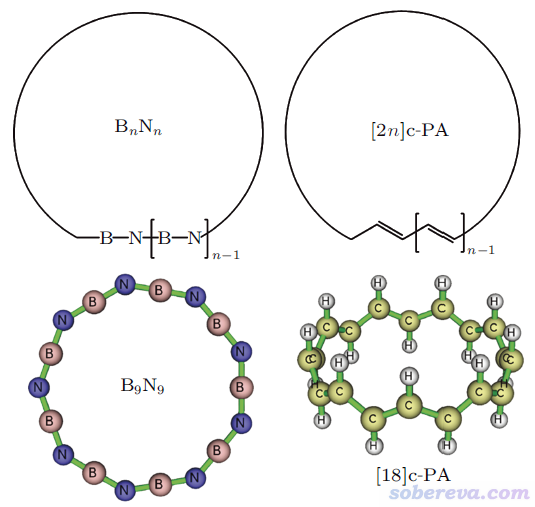
此外,文中還對以下所示的18碳環的等電子體硼-氮環,以及具有單套pi共軛特征的環聚乙炔的環張力做了計算,發現硼-氮環類體系的環張力明顯小于碳環類,而環聚乙炔類體系的環張力則略大于碳環類。文中利用Multiwfn程序(http://www.shanxitv.org/multiwfn)做波函數分析從電子結構角度清晰解釋了它們的環張力與碳環之間存在差異的原因。文中還發現用常用的B3LYP泛函算全局pi共軛的環狀聚合物的合理性較差,E/n隨n的變化明顯不合理。這些方面這里就不多提了,請讀者務必閱讀論文原文。
5 總結
環張力是環狀分子的重要特性。本文簡明扼要地介紹了兩種最常用的計算環狀分子的環張力能的方法,并以[6]CPP和18碳環作為具體例子進行了演示。同聯反應法比較方便省事,但對于一些全局pi共軛的環狀體系,諸如18碳環,則更適合外推法,明顯嚴格得多,同時外推法還很有助于探究環尺寸與環張力之間的關系。還應當注意并不是所有環狀體系都能用這兩種方法之一計算環張力能,比如苯分子,它存在顯著的和其環狀結構緊密相關的六中心鍵,因而環張力本來就是難以被定義的。