使用Multiwfn通過單位球面表示法圖形化考察（超）極化率張量

使用Multiwfn通過單位球面表示法圖形化考察（超）極化率張量

First release: 2020-Apr-10 Last update: 2021-Sep-10

1 前言

如果讀者對（超）極化率的概念還不怎么了解的話，建議先看看《使用Multiwfn分析Gaussian的極化率、超極化率的輸出》（http://www.shanxitv.org/231）中的相關知識。平時在研究分子的（超）極化率的時候，關注的通常只是總大小，以及X、Y、Z方向的總分量，而對于（超）極化率張量的各個具體分量，尤其是非對角元，則通常探究得不多，而非對角元所體現出的（超）極化率的各向異性其實也是很值得探究的。在J. Comput. Chem., 32, 1128 (2011)一文中作者提出了單位球面表示法（Unit Sphere Representation）來可視化第一超極化率張量(beta)，這可以很直觀地全面考察beta張量的特征，特別是能將其各向異性展現出來。

2 原理

在具體介紹單位球面表示法之前先回顧一下beta的定義，看下式：

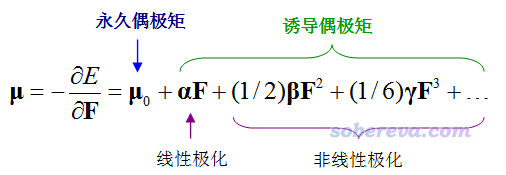
對于均勻外電場來說，靜態的beta的ABC分量的物理意義體現的是從B、C方向同時射入單位強度的電場的耦合作用導致分子偶極矩在A方向上發生變化的一半。如果外場是電磁場，其對應的變化的電場會導致分子的電子密度分布震蕩而發出電磁波，描述分子的這種響應特征是通過動態的beta。比如beta(-(w1+w2);w1,w2)的ABC分量體現的是頻率分別為w1、w2且變化方向分別是B、C的電場，導致分子的偶極矩在A方向上以w1+w2頻率發生震蕩的程度，也正比于由此發出的w1+w2頻率的電磁波的強度。若w1=w2，這對應的是二次諧波生成(SHG)過程。

為了能一目了然地表現向分子的什么方向施加的兩個電場的耦合作用會導致分子的偶極矩在什么方向以何種程度發生變化，單位球面表示法定義了βeff矢量，如下所示。

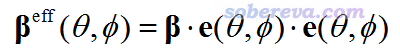
其中e(θ,φ)是從原點朝向球極坐標的(θ,φ)方向的單位矢量。beta既可以是靜態的也可以是動態的，原文里只將此方法用在了對應SHG的beta的情況，并且把βeff稱為“有效SHG偶極”或“有效非線性偶極”。為了避免含糊，筆者下面給出βeff的i分量的具體的計算表達式

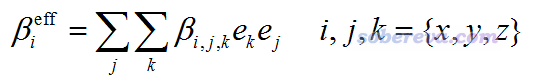
結合前面給出的偶極矩和beta的關系式可知，基于beta(-2w;w,w)計算的βeff(θ,φ)矢量，體現出的是在(θ,φ)方向上的兩個變化頻率皆為w的電場共同作用所導致的偶極矩以2w頻率震蕩的方向和大小。

對一個特定半徑的球面上每個點都計算βeff矢量，根據矢量方向和大小繪制出箭頭并著色（箭頭起點設在球面相應位置），得到的就是所謂的單位球面表示法對應的圖像了。

在Multiwfn程序解析Gaussian的polar任務的輸出文件時還會給出beta_X、beta_Y、beta_Z，表達式如下：

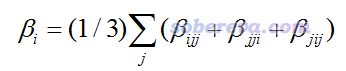
這在單位球面表示法的文章里叫做“矢量表示”（Vector Representation），可以通過繪制一個箭頭來圖形化展現它。由其表達式可見，這種表示相當于把不同方向施加電場的耦合效果做了平均化，因此忽略掉了各向異性，比如beta_X中包含了beta_XXX、beta_XYY、beta_XZZ等，體現了不同方向的外加電場的耦合作用導致X方向偶極矩的平均變化程度。諸如其中的beta_XXX相當于兩個外電場方向與誘導偶極矩方向是共線的情況，beta_XYY或beta_XZZ相當于是垂直的情況，等等。

類似地，筆者將單位球面法推廣到極化率和第二超極化率：

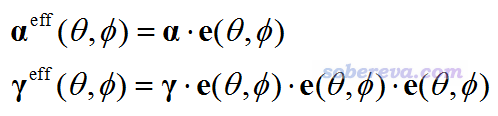
例如基于w頻率的極化率（alpha）計算的αeff(θ,φ)矢量體現的是在(θ,φ)方向施加的變化頻率為w的電場所引起的分子偶極矩以w頻率變化的方向和大小。而γeff(θ,φ)體現的則是(θ,φ)方向的三個電場的耦合所導致的分子偶極矩變化情況。

3 Multiwfn做單位球面表示法分析的功能

上述方法已經被筆者實現在了Multiwfn程序中（必須是2020-Apr-10及以后更新的版本才有），程序可以在主頁http://www.shanxitv.org/multiwfn免費下載，不了解Multiwfn者建議參看《Multiwfn FAQ》（http://www.shanxitv.org/452）和《Multiwfn入門tips》（http://www.shanxitv.org/167）。此程序可以將單位球面表示法用于極化率、第一/第二超極化率，對第一超極化率還可以用矢量表示法。

使用當前功能應當在Multiwfn啟動時載入一個能給Multiwfn提供結構信息的文件（因為Multiwfn要判斷分子半徑來確定箭頭的繪制位置），可以用pdb、gjf、xyz等各種格式，見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。Multiwfn做本文介紹的分析時需要從.txt文件中讀取（超）極化率，可以讓Multiwfn解析Gaussian的polar任務的輸出文件來產生，也可以自行提供。此文件里需要記錄所有張量的分量，內容是自由格式，單位是a.u.，張量元的記錄順序如下（用Fortran的隱do循環便于表示）
極化率：((alpha(i,j),j=1,3),i=1,3)
第一超極化率：(((beta(i,j,k),k=1,3),j=1,3),i=1,3)
第二超極化率：((((gamma(i,j,k,l),l=1,3),k=1,3),j=1,3),i=1,3)
其中越靠內的序號越優先循環。比如極化率張量的記錄順序是(1,1),(1,2),(1,3),(2,1),(2,2)...(3,3)。

Multiwfn的這個功能會產生可視化程序VMD的作圖腳本，在VMD里執行腳本即可得到瞬間得到圖像。VMD可以在此處免費下載：http://www.ks.uiuc.edu/Research/vmd/。

下面就通過實例演示怎么通過Multiwfn+VMD對實際體系得到單位球面和矢量表示法的圖像。Gaussian用的是G16 A.03版。

4 可視化第一超極化率的例子：CH3NHCHO

本例我們對單位球面表示法原文里考察的CH3NHCHO體系進行繪制，這個體系相當于蛋白質的肽鍵部分區域。用的計算級別和原文完全一樣，即優化的級別是B3LYP/6-311++G**（加彌散純屬多余），算（超）極化率的級別是HF/6-311++G**（顯然這個級別算的beta是很垃圾的，這里用這個的目的僅僅是為了試圖重復原文里的圖而已）。即便用相同的級別，也不要指望我們的結果能和原文精確相同，因為作者用的GAMESS-US里的B3LYP和Gaussian里的并不完全相同（VWN泛函的版本有異），而且積分格點等數值層面上也有各種細節的不同。

首先，我們對此體系做polar任務計算alpha和beta，外場頻率用450 nm和1030 nm，和原文一致。輸入文件如下，結構是在B3LYP/6-311++G**下已經優化好的。為了讓Multiwfn能解析輸出文件里的信息，#P是必須寫的。由于原文考察的是SHG的情況，所以這里寫了=DCSHG。

#P HF/6-311++g(d,p) polar=DCSHG CPHF=rdfreq
[空行]
B3LYP/6-311++G** opted
[空行]
0 1
C                 -1.42185400    0.48434600    0.00000000
H                 -1.99137900    1.41345100    0.00000000
H                 -1.68745700   -0.09936700    0.88452400
H                 -1.68745700   -0.09936700   -0.88452400
N                  0.00000000    0.80427900    0.00000000
C                  0.95655400   -0.15841500    0.00000000
H                  0.29333200    1.76830000    0.00000000
O                  0.73560300   -1.35373200    0.00000000
H                  1.97993900    0.26130100    0.00000000
[空行]
450nm 1030nm

計算的輸出文件已經提供為Multiwfn文件包里的examples\polar\CH3NHCHO\polar.out。

我們先用Multiwfn把對應1030 nm的SHG形式的beta提取出來成為.txt文件。啟動Multiwfn然后輸入
examples\polar\CH3NHCHO\polar.out
200 //其它功能（Part 2）
7 //解析Gaussian的polar任務的輸出
-1 //要求程序解析含頻的（超）極化率
-4 //要求程序解析后把（超）極化率導出成當前目錄下的.txt文件
1 //開始解析。并且當前對應的是有三階解析導數的情況，如KS-DFT
2 //如提示所示，2號對應的是1030 nm的情況
2 //解析Beta(-2w;w,w)形式
n //程序問你是否做《使用Multiwfn計算與超瑞利散射(HRS)實驗相關的量》（http://www.shanxitv.org/499）文中介紹的分析，這里跳過

現在極化率張量和第一超極化率張量已經分別被導出為了當前目錄下的alpha.txt和beta.txt，感興趣的話可以打開看看。現在可以退出Multiwfn。

前面說了，用Multiwfn做本文的分析時應當在一開始載入一個能給Multiwfn提供分子結構信息的格式，實際上也可以直接讓Multiwfn從Gaussian的輸出文件中讀取分子結構。為此，修改Multiwfn目錄下的settings.ini里的iloadGaugeom為1，然后啟動Multiwfn，依次輸入
examples\polar\CH3NHCHO\polar.out
300 //其它功能（Part 3）
3 //用單位球面和矢量表示法可視化（超）極化率

現在在屏幕上可以看到很多選項用來設置，包括球面上箭頭的半徑、比例因子（數值越小箭頭越短）、是否給這些箭頭著色、圓球的半徑（默認是根據分子直徑自動調節）、球面上箭頭的數目。還可以設置矢量表示法的箭頭的半徑和比例因子。這些大家可以嘗試自行調節以達到更滿意的效果，本例就直接用默認值。

現在選擇選項2，從屏幕上的提示可見由于程序發現當前目錄下有beta.txt，因此就直接從中讀取beta張量了，如果沒有這個文件的話程序會讓你輸入含有beta張量的文本文件的路徑。從屏幕上還看到球面上實際箭頭有566個，并且在當前目錄下輸出了beta.tcl和beta_vec.tcl，這倆都是VMD的作圖腳本，執行前者會繪制單位球面表示法的圖像，執行后者會繪制矢量表示法的圖像。屏幕上還看到beta_X、beta_Y、beta_Z的值，它們乘上比例因子就相當于矢量表示法的箭頭的長度。

為了能在VMD中把分子結構也繪制出來便于考察，我們讓Multiwfn導出pdb文件。接著輸入以下命令
0 //退出當前功能
0 //返回到主菜單
100 //其它功能（Part 1）
2 //導出文件
1 //導出pdb文件
CH3NHCHO.pdb
現在當前目錄下就有了CH3NHCHO.pdb，可以把Multiwfn關了。

把當前目錄下的beta.tcl和beta_vec.tcl都移動到VMD目錄下，啟動VMD，然后在文本窗口輸入source beta.tcl命令運行beta.tcl腳本，此時單位球面表示法的圖就顯示出來了，再輸入source beta_vec.tcl，矢量表示法的箭頭也繪制出來了。最后，把CH3NHCHO.pdb拖到VMD的VMD Main窗口里載入，然后選Graphics - Representation，把Drawing method設為CPK，此時圖像如下：

此圖和球面表示法原文J. Comput. Chem., 32, 1128 (2011)里的圖2(e)幾乎完全一樣，而且比原文的效果更好，因為原文中的箭頭分布并不均勻。圖中箭頭的顏色按照藍-白-紅變化，箭頭越短越藍，越長越紅，箭頭實際長度對應于的βeff(θ,φ)矢量的模乘上自設的比例因子。

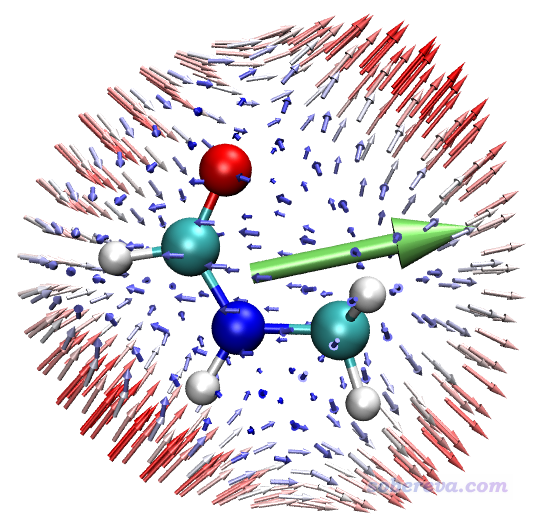
給出這種圖的時候建議同時給出不同角度，以便看得全面，下圖是另一個角度的。為了把分子另一側的箭頭淡化以避免擾亂視覺，筆者開了霧化效果，關于這點參見《VMD初始化文件(vmd.rc)我的推薦設置》（http://www.shanxitv.org/545）。

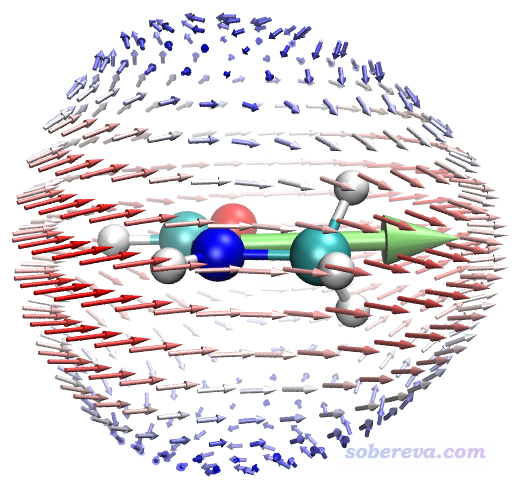
從本例的圖能看出什么？下面把3個特征位置標注了出來予以說明

圖中1號位置體現的是，當施加的兩個頻率為w的電磁場的電場變化方向是順著粉色箭頭時，其耦合作用會導致在相同方向產生強度顯著的變化頻率為2w的誘導偶極矩，由于電場和誘導偶極矩方向相同，因此這個方向沒有各向異性。2號位置體現的是沿著粉色箭頭方向變化的兩個外電場的耦合作用所產生的誘導偶極矩方向是與之相反方向的。3號位置體現的是兩個按照粉色箭頭變化的外電場的耦合作用產生的誘導偶極矩方向是朝右的，和外電場變化方向正好呈90度角，這就體現出顯著各向異性了，如果不作這種圖很難了解這一點。注意，這種圖的箭頭的起點的絕對位置和原子的絕對坐標毫無關系，因為球的半徑是我們隨意設的（程序默認的是比分子大一圈）。上圖標注的粉色箭頭都是從內朝外按球面的法矢量方向畫的，即對應球面相應位置的e(θ,φ)方向，分析球面上其它位置的箭頭特征的時候也需要這么分析。

上圖中的綠色箭頭體現了(beta_X,beta_Y,beta_Z)矢量方向，亦即體現出了分子beta的整體取向。可見綠色箭頭的方向和球面上所有箭頭的總趨勢（矢量和）相同，都是朝右。顯然，這種矢量表示法所展現的信息遠沒有球面表示法那么豐富，細節無法體現。

原文里還有其它一些體系的球面表示法的例子，感興趣的讀者可以看看。原文做這種分析用的是matlab程序結合paraview可視化，遠不如本文介紹的做法方便，而且作者還沒把程序公開。

5 可視化極化率的例子：18碳環

對于18碳環這個電子結構十分特殊的新穎體系，筆者做了很系統的研究，所有已發表的文章匯總見http://www.shanxitv.org/carbon_ring.html。其中也包括對極化率、第二超極化率的研究，已發表于Chem. Asian J., 16, 56 (2021) DOI: 10.1002/asia.202100589，介紹見《全面揭示各種尺寸的碳單環體系的獨特的光學性質》（http://www.shanxitv.org/608）。下面以此體系為例，將單位球面表示法應用于靜態的alpha和gamma，看看這種分析對這種情況能有什么實際價值。本例的輸入文件如下，就是上面提到的我的論文里用的原始輸入文件，此任務將計算靜態的alpha、beta、gamma。

#p wb97xd/gen polar=gamma
[空行]
wb97xd/def-TZVP opted
[空行]
0 1
C                  0.61036100    3.64174700    0.00000000
C                 -0.61036100    3.64174700    0.00000000
C                 -1.87330600    3.18207300    0.00000000
C                 -2.80843400    2.39740800    0.00000000
C                 -3.48043300    1.23347100    0.00000000
C                 -3.69240900    0.03129400    0.00000000
C                 -3.45902600   -1.29228500    0.00000000
C                 -2.84866500   -2.34946200    0.00000000
C                 -1.81910300   -3.21336700    0.00000000
C                 -0.67199900   -3.63087900    0.00000000
C                  0.67199900   -3.63087900    0.00000000
C                  1.81910300   -3.21336700    0.00000000
C                  2.84866500   -2.34946200    0.00000000
C                  3.45902600   -1.29228500    0.00000000
C                  3.69240900    0.03129400    0.00000000
C                  3.48043300    1.23347100    0.00000000
C                  2.80843400    2.39740800    0.00000000
C                  1.87330600    3.18207300    0.00000000
[空行]
0.0
[空行]
@/sob/LPol-ds.gbs/N

其中坐標后面的0.0代表只考慮靜態的情況（外場為零頻）。本例用的LPol-ds是能夠高精度表現（超）極化率的基組，不是Gaussian內置的，所以通過外部文件讀取，可以在這里獲取：《各種Sadlej基組的Gaussian格式的定義》（http://www.shanxitv.org/345）。

啟動Multiwfn，然后輸入
examples\polar\C18\gamma.out //上面輸入文件的輸出文件
200 //其它功能（Part 2）
7 //解析Gaussian的polar任務的輸出
-4 //要求程序解析后把（超）極化率導出成當前目錄下的.txt文件
7 //解析polar=gamma的任務
此時當前目錄就有了alpha.txt和gamma.txt。接著輸入：
0 //退出當前功能
0 //返回主菜單
300 //其它功能（Part 3）
3 //用單位球面和矢量表示法可視化（超）極化率
-3 //修改圓球上箭頭的比例因子
0.005 //這比默認的比例因子小很多，因為C18的極化率很大。這個值需要反復嘗試直到令作出的圖的箭頭長度比較合適
-5 //修改矢量表示法箭頭的比例因子
0.01
1 //對極化率進行分析，將會從當前目錄下的alpha.txt中載入極化率張量

現在當前目錄下就有了alpha.tcl和alpha_vec.tcl，將之挪到VMD目錄下，然后運行source alpha.tcl，再運行source alpha_vec.tcl。之后和前例一樣通過主功能100的子功能2導出當前體系的pdb文件，并把其載入VMD并顯示。此時圖像如下（適當用了霧化）

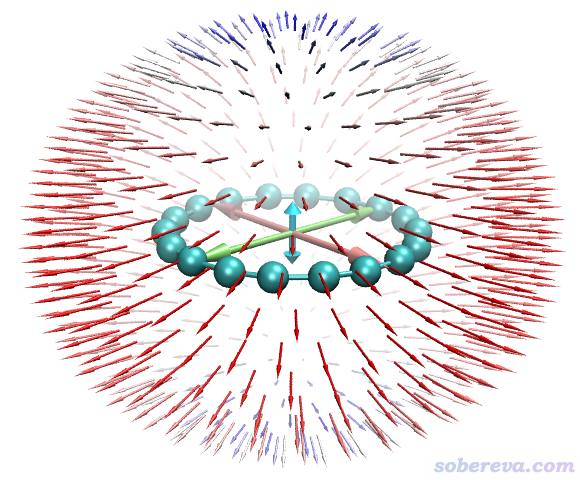
這個圖中分布于球面的小箭頭體現由分子中心向四面八方都施加同樣強度的外電場時導致的分子的偶極矩的變化。由圖可以清晰地看出18碳環在垂直于環平面方向的極化率較小，而在平行于分子的方向極化率很大。這很容易理解，因為18碳環分子平面上有非常豐富、高度離域的pi電子（in-plane和out-plane兩類pi電子共36個），故平行于體系加外電場必然能高度極化pi電子分布，從而產生顯著的誘導偶極矩。從Multiwfn的主功能200的子功能7解析的數據的時候可見alpha_ZZ（垂直于環平面方向）為97.7 a.u.，而alpha_XX和alpha_YY（平行于環平面方向）高達392 a.u.。

上圖中央的三個雙向大箭頭的長度展現的是X、Y、Z方向極化率的總大小（alpha_X、alpha_Y、alpha_Z），分別由下面的公式計算。大箭頭的長度使讀者便于清晰地對比這三個方向的極化率的大小。注意這種極化率的矢量表示法和之前看到的beta的矢量表示法明顯不一樣，前者只體現每個軸向的大小，不體現方向性（從球面上的箭頭也可見極化率的情況是以中心對稱分布的）。

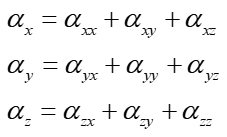
接下來再用單位球面表示法考察一下C18的gamma。在主功能300的子功能3里輸入
-3 //修改圓球上箭頭的比例因子
1E-5 //比默認的值小得多，這是因為gamma的數量級很大
-5 //修改矢量表示法箭頭的比例因子
0.00005
3 //對第二超極化率進行分析，將會從當前目錄下的gamma.txt中載入極化率張量
現在當前目錄下就有了gamma.tcl和gamma_vec.tcl，在VMD里執行這倆腳本，圖像如下

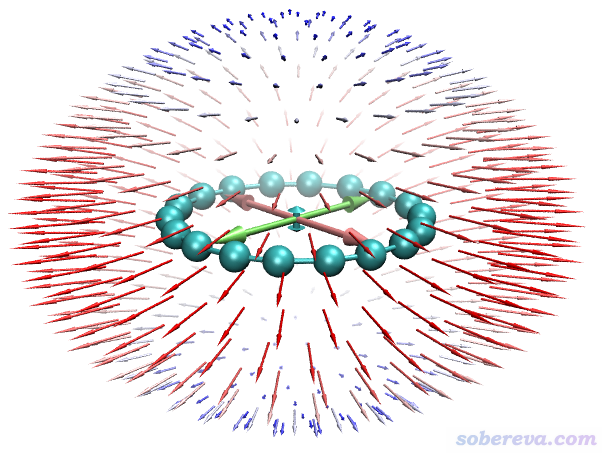
由球面上的箭頭可見gamma的特征和alpha類似，都是順著分子平面的方向大，垂直于分子平面的方向小。此圖中，球面上的箭頭體現的是由內向外以球面法向量方向施加3個電場的耦合作用導致體系偶極矩的變化矢量。

上圖中平行于三個笛卡爾軸的雙向大箭頭對應的是gamma的矢量表示法，其長度直觀體現在X、Y、Z三個方向的gamma的總大小（gamma_X、gamma_Y、gamma_Z），計算方式如下

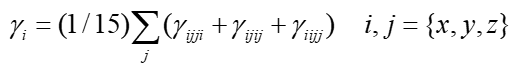
對18碳環我們不分析beta，因為這種中心對稱體系的beta精確為0。

6 總結

本文介紹了一種在研究（超）極化率問題中非常實用的單位球面表示法，并結合實例介紹了怎么通過Multiwfn和VMD程序非常容易地實現這種分析并且得到效果酷炫的圖像。這個方法幾乎在任何體系的（超）極化率研究中都可以使用，在文章里給出這樣的圖像明顯能給文章增光添彩，令分析更深入，因此非常推薦大家使用。

前面提到的筆者的Chem. Asian J., 16, 56 (2021)一文，以及在《理論設計由18碳環與鋰原子構成的電場可控的光學開關》（http://www.shanxitv.org/630）中介紹的筆者的Carbon, 187, 78 (2022)一文，還有在《深入揭示18碳環的重要衍生物C18-(CO)n的電子結構和光學特性》（http://www.shanxitv.org/640）中介紹的Chem. Eur. J., 28, e202103815 (2022)一文都利用了本文的做法分析了（超）極化率，是單位球面表示法的極好的應用例子，十分推薦仔細閱讀并作為范例進行引用。

有一個很值得注意的地方在這里提醒一下。Multiwfn解析Gaussian的polar關鍵詞給出的alpha、beta都是解析的標準朝向下的，對于gamma則是解析輸入朝向下的（因為Gaussian沒輸出標準朝向下的）。如果不懂什么叫輸入朝向和標準朝向，看《談談Gaussian中的對稱性與nosymm關鍵詞的使用》（http://www.shanxitv.org/297）中的相關說明。載入到VMD里的分子的結構應當和分析的（超）極化率的朝向一致，否則會造成誤判。前面的例子沒有區分這點，是因為這些例子中做polar任務的gjf文件中的坐標取自幾何優化任務輸出文件中的標準朝向下的結果，因此坐標本身就已經是在標準朝向下了，換句話說這些polar任務在做的時候輸入朝向和標準朝向是等同的。Multiwfn的iloadGaugeom=1時從Gaussian輸出文件中優先載入輸入朝向的結構（找不到的時候才會載入標準朝向的，此時屏幕上會有提示），而iloadGaugeom=2時則載入標準朝向的。GaussView打開輸出文件時載入的總是標準朝向的。