談談溫度、壓力、同位素設定對量子化學計算結果產生的影響
文/Sobereva @北京科音
First release: 2018-Jun-1 Last update: 2021-Feb-27
經常有量子化學初學者問諸如這種問題:怎么計算特定溫度/壓力下體系的結構、重水和輕水的結構有什么區別。每次回復都比較麻煩,索性寫一個小文章專門談一下溫度、壓力、同位素設定會對哪些常見的量子化學問題計算結果產生影響、對哪些完全沒有影響。為討論方便,這里假定用戶用的是Gaussian,其可以通過pressure、temperature關鍵詞分別設定壓力和溫度,還可以設定同位素,比如把坐標部分的H寫為H(iso=2)就等于用氘。本文的討論對于其它各種量子化學程序也是完全適用的,因為原理都是共通的。下文中所說的單點能意指電子能量,不知道什么叫電子能量的話看《談談該從Gaussian輸出文件中的什么地方讀電子能量》(http://www.shanxitv.org/488)。
1 壓力設定產生的影響
在各種Gaussian可以做的任務中,壓力設定僅僅會對freq任務產生的熱力學數據產生影響。更具體來說,影響的僅僅是熱力學數據中的熱力學校正量部分中的平動熵部分。在《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552)介紹的筆者開發的Shermo程序手冊的附錄部分給出了各種熱力學校正量的詳細的表達式,可見其中只有平動熵部分才依賴于壓力(P)。之所以平動部分會依賴于壓力設定,這本質上是因為程序計算熱力學數據的時候是把體系當做理想氣體考慮的,此時平動部分的公式是通過三維勢箱模型推導出來的,而三維勢箱的體積V,正是根據大家熟知的PV=nRT的理想氣體公式算出來的,其中牽扯到P。這里再強調一下,量子化學在計算一個體系的時候,是把體系當做處于真空狀態來計算的。而計算熱力學數據時,考慮的是處于理想氣體狀態下的1mol的當前體系。既然是理想氣體,就說明忽略了分子間一切相互作用,因此不管壓力設多少,始終都是按理想氣體算的,改變的僅僅是平動項貢獻里的參數P而已。所以千萬別以為在高壓下體系是凝聚相的,于是你把pressure設得很大,量化程序就把當前體系按照凝聚相考慮。
壓力對熱力學數據以外的任何量子化學程序計算結果(比如優化的結構、振動頻率、電子激發能、NMR、偶極矩等等)都不產生絲毫影響,原因從計算原理上稍微想一下就知道。比如計算單點能,這要求解分子體系的電子薛定諤方程,而這方程里哪項體現壓力的影響了?既然不依賴于壓力,算出來的能量啊、波函數啊,以及各種相關的量都明顯不可能受壓力設定影響。做計算一定要懂一些最基本的原理(PS:這些從事計算必備的知識在北京科音量子化學培訓班里都會講)。
在第一性原理計算領域,研究的主要都是周期性體系,這種情況壓力確實會產生影響,比如不同壓力設定下做晶胞優化會得到不同的晶胞參數,這是因為計算的體系本身就是凝聚相體系,會對壓力設定直接產生響應。
2 溫度設定產生的影響
溫度對量化計算能產生的影響遠比壓力設定多。下面分情況說。2.1 溫度對結構的影響
化學體系的電子薛定諤方程中根本就沒有溫度這一項,顯然不管用什么理論方法計算,得到的單點能、波函數都是完全與溫度設定無關的。而勢能面就是各種幾何結構下單點能的集合,因此勢能面也與溫度完全無關。幾何優化要找的就是勢能面上的駐點(一般感興趣的是其中的極小點和過渡態),因此溫度設定根本就不可能對opt任務優化出的結構有絲毫影響。
網上有一個嚴重以訛傳訛,令無數初學者信以為真的說法:幾何優化得到的是0K下的結構。這明顯是在胡說八道。哪怕是在0K下,由于存在零點能,因此分子依然有內振動,這個道理學過量子力學處理諧振子模型的人都懂。既然還在不斷振動,就意味著沒有確切的核坐標,怎么來“優化”得到?得到什么?我們做幾何優化得到的是勢能面的極小點,而“極小點”和“勢能面”不是實際可觀測的,而是我們使用了玻恩奧本海默近似后得到的便于理論討論而虛構出來的概念。說“極小點”這個概念的時候,意味著已經徹底舍棄了“溫度”這一概念,哪怕0K也算溫度。
但值得一提的是,量化上可以計算的一個和結構有關的量是和溫度有關的,這稱為振動平均結構。只要有溫度,分子就在振動,可以對振動過程取個平均結構。在諧振近似下,由于勢函數相對于平衡坐標(優化出來的坐標)是對稱的,因此振動平均結構和極小點結構完全相同;而在非諧振近似下,就可以不再是對稱的了,此時振動平均結構就會偏離極小點,而且溫度越高,從經典力學角度看,由于核具有更大動能、運動范圍更廣,因此與極小點結構偏離得越多。
在Gaussian中可以做非諧振計算,比如對HF使用# B3LYP/def2SVP opt freq=anharm temperature=1000關鍵詞,則輸出文件里非諧振計算部分就會輸出平衡結構、0K下和當前設定的溫度下的振動平均結構:
平衡結構:0.9247埃
0K振動平均結構:0.940614埃
1000K振動平均結構:0.940704埃
為了便于直觀理解,在下面的HF解離曲線圖上,用粉色豎線標注了平衡結構位置,用藍色豎線標注了0K下振動平均位置。可見由于此勢能面的非對稱性,導致振動平均鍵長大于平衡鍵長。
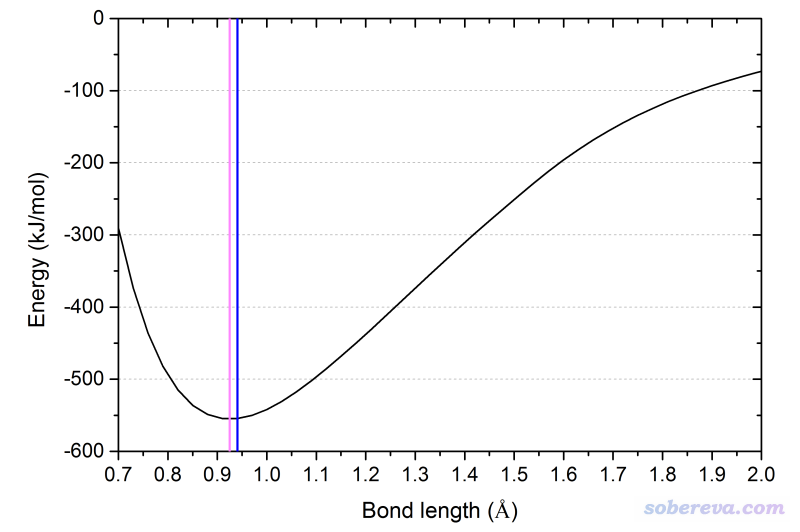
常規量化計算不會去討論振動平均結構,而且計算振動平均結構要做非諧振計算,對稍大一丁點的體系都是極為耗時的。平時就用極小點結構說事就夠了。
2.2 溫度對熱力學量的影響
溫度對熱力學數據的影響是全方位的,量化程序做振動分析給出的內能、焓、熵、自由能、熱容全都依賴于溫度,這通過前面提到的Shermo程序(http://www.shanxitv.org/soft/shermo)文檔附錄里的公式一看便知。再多說幾句,實際上有一個概念叫自由能面,就是所有結構下計算的自由能的集合。通常來說勢能面(也可以叫電子能量面)主導了自由能面的形狀,但熵效應明顯的時候往往也有定性的偏差。自由能面上也可以定義一階鞍點、極小點這樣的概念,由于自由能是依賴于溫度的,因此不同溫度下的自由能面也是不同的,相應地,自由能面上的一階鞍點、極小點位置也不同。自由能面上的一階鞍點是很有意義的,因為在變分過渡態理論中,計算勢壘的位置就應該取自由能面上的一階鞍點,用這個點來定義過渡態這個概念比用勢能面上的一階鞍點意義更充分、更嚴格。但由于在自由能面上優化很復雜(耗時極高、沒有解析梯度),一般量化程序不支持,故人們平時都是將勢能面上的一階鞍點視為過渡態。
2.3 溫度對光譜的影響
計算分子振動頻率需要的是極小點處勢能面的導數信息,計算過程完全不牽扯溫度,因此溫度也不可能對freq任務算出來的振動頻率有絲毫影響。與振動模式相關的紅外強度、拉曼活性,都是以能量對外電場、坐標的導數方式計算的,顯然也根本不牽扯溫度。值得一提的是模擬理論拉曼光譜時應當基于拉曼強度進行展寬,而不是直接基于Gaussian直接給出的拉曼活性進行展寬,這點在《使用Multiwfn繪制紅外、拉曼、UV-Vis、ECD和VCD光譜圖》(http://www.shanxitv.org/224)中有明確說明。將拉曼活性轉化為拉曼強度的過程中,需要輸入溫度(本質上是因為要考慮玻爾茲曼平均),因此溫度會影響模擬得到的拉曼光譜。
我們平時研究的紅外光譜都是對應振動基態到第一振動激發態的躍遷,相應的吸收稱為基帶。但當溫度較高時,體系會有一定比率出現在振動激發態上,處于振動激發態的體系向更高振動激發態的躍遷對應紅外光譜上的熱帶。要想計算對應熱帶的吸收頻率,必須做非諧振計算才能得到有意義的結果。
在《使用Multiwfn繪制構象權重平均的光譜》(http://www.shanxitv.org/383)中提到,對于可能有較多熱可及(即在當前溫度下容易發生互變)的構象、構型的體系,繪制光譜時要考慮Boltzmann權重,而這個權重是直接依賴于溫度的,見《根據Boltzmann分布計算分子不同構象所占比例》(http://www.shanxitv.org/165)。因此,從這個角度上,溫度會影響模擬的光譜。但溫度的這種影響顯然不是量化程序里寫個temperature關鍵詞就了事的,看完以上文章就知道具體該怎么做了。
說得更遠一些,也可以藉由動力學來考慮溫度對光譜的影響。比如可以對一個體系跑動力學,每隔一定幀數計算一次UV-Vis光譜,然后對光譜做時間平均。由于溫度會顯著影響動力學過程,因此溫度會的影響會體現在最終的光譜上。
2.4 溫度對其它問題的影響
現在多數主流量化程序都能做從頭算動力學(AIMD),溫度顯然直接影響模擬結果。但是對于Gaussian,寫temperature關鍵詞沒有任何用處,得用IOp來專門地設定熱浴。溫度對于IRC不可能有任何影響,因為IRC是質量權重坐標上的能量極小路徑,能量極小路徑是勢能面上的拓撲特征,和溫度一點關系沒有。
量子化學上能計算的問題太多,顯然不可能逐一討論,稍微了解一下原理,自然而然就能判斷出溫度是否能對當前研究的問題產生影響。如果自己理論知識不足,找個最簡單的體系算算試試,對比一下結果,立刻就明白了。
3 同位素設定產生的影響
不同同位素體現在原子核質量不同。我們一般用的量化程序都是在玻恩奧本海默近似下做的計算。由于要求解的電子薛定諤方程里面根本沒有原子核質量這一項,所以同位素設定完全不影響勢能面,顯然單點能,以及優化出來的極小點/過渡態結構等都不會受到同位素的影響。
熱力學數據計算結果和同位素設定密切相關。比如平動貢獻部分,平動配分函數里直接就有個體系總質量項。轉動貢獻部分,需要的轉動慣量也直接依賴原子質量。由于前面說了,不同同位素下振動頻率明顯不同,因此熱力學數據的振動部分貢獻也依賴同位素設定。Gaussian在計算熱力學數據的時候用的是豐度最大的同位素,但實際上嚴格來講,應當把所有同位素的情況的熱力學數據都算出來,然后按照豐度取平均。但這么做實在麻煩,通常影響也不大,所以一般不這么做(有的時候考慮一下還是有益的,比如Cl,豐度最大的Cl-35和次大的Cl-37比例是3:1,次大的占比也不小了)。
振動頻率是怎么算出來的,在《基于fch中的Hessian矩陣計算振動頻率的簡單程序Hess2freq》(http://www.shanxitv.org/328)給出了詳細描述。在最簡單的諧振近似下,由于振動頻率是力常數矩陣的本征值折算的,而力常數矩陣又是質量權重坐標下的Hessian矩陣,牽扯到了原子質量,故同位素設定直接影響振動頻率。而且與振動模式對應的正則坐標是力常數矩陣的本征矢,而紅外強度、拉曼活性分別對應于偶極矩、極化率對正則坐標的一階導數,因此紅外強度和拉曼活性也受到同位素的影響。
例如,在B3LYP/def2-SVP下,HF的諧振頻率是4080.4 cm-1,紅外強度是94.6 KM/Mole,而氘代后(即DF),頻率減小到了2958.1 cm-1,紅外強度減小到了49.7 KM/Mole。之所以頻率變低了很容易理解,因為HF和DF的極小點位置相同,此處勢能面曲率相同,可以理解為振動的源動力相同,但由于氘比氕更重,顯然振動更慢。
類似地,其它的振動譜,如振動圓二色譜(VCD)、拉曼光學活性譜(ROA),也都依賴于同位素設定。至于電子光譜,跟原子質量毫無直接關系,因此不受任何影響。除非是要繪制比如構象權重的電子光譜,由于同位素設定直接影響各個構型/構象的自由能,進而影響分布比例,此時同位素的影響才會體現光譜上。
雖然如前所述,同位素設定不影響優化出來的幾何結構,但由于影響了振動特征,顯然會影響振動平均結構。
同位素設定也會影響IRC。因為IRC是質量權重坐標下的能量極小路徑,既然涉及質量權重了,肯定結果會依賴于原子質量。為了便于了解這一點,下面把HCN->CNH氫遷移完整IRC中的所有點疊加到一起顯示。繪制這個圖的時候,利用了《Gaussian的IRC任務輸出轉換為.xyz軌跡文件的工具》(http://www.shanxitv.org/285里的)中的GauIRC2xyz工具將IRC軌跡轉化為了xyz軌跡格式,然后載入到了VMD里以多幀疊加方式進行顯示。
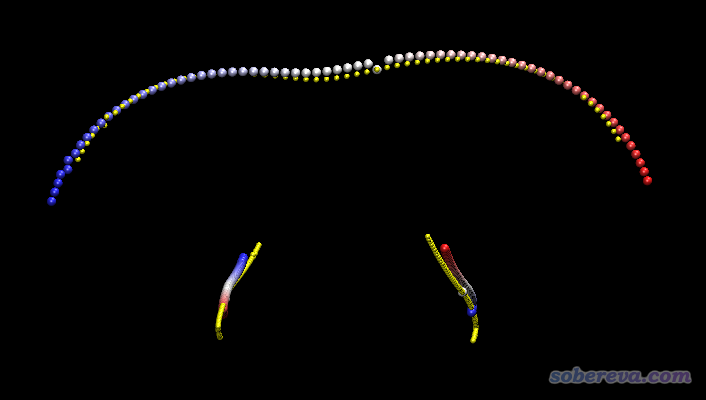
上圖中,上方是氫遷移的軌跡,下方是碳和氮移動的軌跡。黃色圓球對應的是氘代的情況,彩色圓球對應的是沒有氘代的情況,原子按照紅->白->藍的軌跡移動。可見,氘代前后IRC確實發生了不小變化。
同位素設定對于AIMD模擬明顯也會產生影響,比如最常用的BOMD形式,本質上用的就是高中就學過的牛頓方程,里面明顯牽扯到原子質量。
對于其它絕大部分量化上研究的問題,同位素設定都不會產生任何影響,這里就不再一一討論了。
實際上,如果要進一步改進玻恩奧本海默近似下的計算結果,可以給原先計算的能量上加上對角波恩奧本海默校正項(DBOC, Diagonal Born-Oppenheimer correction),其表達式如下:
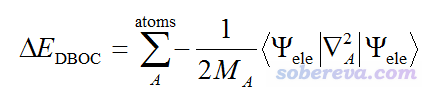
可見其中牽扯到原子質量。因此考慮DBOC項的話,同位素設定其實也是會影響單點能以及優化出的幾何結構的。但是DBOC的數量級非常非常小,比平時研究能用到的最高級的理論方法和基組造成的誤差還小,而且只對很輕的元素才可察覺得到,故平時研究根本不考慮。能計算DBOC的程序非常少,其中相對知名的也就是CFOUR,介紹見《CFOUR程序的編譯和使用方法簡介》(http://www.shanxitv.org/150),它可以在HF、MP2、CCSD級別下算DBOC,如果再結合MRCC還能在更高級別下算。CFOUR在考慮DBOC下優化時只能用數值梯度。J. Chem. Phys., 118, 3921 (2003)對一些體系的DBOC效應進行了研究,對于BH(氫化硼),DBOC效應對平衡鍵長的影響才區區0.0007埃,對諧振頻率的影響才2 cm-1。對于更重的原子影響會更微乎其微。可見平時研究沒必要考慮DBOC,對于初學者來說,就簡單認為同位素質量根本不影響能量和幾何結構就完了。
最后再強調一下,所有能夠影響勢能面的設定,對于上面提到的所有任務都會產生直接影響,包括理論方法和基組的選擇、考察的電子態、溶劑效應的考慮、泛函積分格點的設定、雙電子積分精度的閾值(Gaussian里的int=acc2e)、相對論效應的考慮、外電場/背景電荷的設定、凍核近似的設置,以及是否使用DFT-D、Counterpoise等對能量的校正等。其它設定如果不知道是否會產生影響,just try。至于SCF收斂限這種問題,由于對能量及其導數的計算影響不是系統性的而是隨機性的,所以姑且不將之作為會影響勢能面的設定,只要實際計算的時候別設得太松就行。