使用Multiwfn展現過剩電子(excess electron)并計算它的回轉半徑
使用Multiwfn展現過剩電子(excess electron)并計算它的回轉半徑
文/Sobereva@北京科音 2023-Jan-30
1 過剩電子的展現
化學領域里的過剩電子(excess electron)通常是指定有電子比較集中地出現在化學體系的某一塊區域。過剩電子沒有唯一展現方式,有很多手段都可以展現其分布,比如電子密度差(參考《使用Multiwfn作電子密度差圖》http://www.shanxitv.org/113)、自旋密度(參考《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》http://www.shanxitv.org/353)、ELF或LOL(參考《ELF綜述和重要文獻小合集》http://bbs.keinsci.com/thread-2100-1-1.html)、定域化軌道(參考《Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比》http://www.shanxitv.org/380)、對UKS波函數做雙正交化后的SOMO軌道(參考《用于非限制性開殼層波函數的雙正交化方法的原理與應用》http://www.shanxitv.org/448),等等,這些都可以通過波函數分析程序Multiwfn(http://www.shanxitv.org/multiwfn)輕易地考察。不了解Multiwfn的話看《Multiwfn FAQ》(http://www.shanxitv.org/452)和《Multiwfn入門tips》(http://www.shanxitv.org/167)。
下面給出兩個帶有過剩電子體系的例子,一個是8個氟取代的立方烷的陰離子,一個是四個水分子結合一個額外電子構成的水合電子團簇,下圖用三種不同方式對過剩電子的分布做了展現,都是Multiwfn直接繪制的圖。ρs代表自旋密度,Δρ是陰離子的電子密度減去相同結構下中性狀態的電子密度得到的密度差,φLMO是指軌道定域化得到的能量最高的定域化alpha占據軌道。波函數是用Gaussian在ωB97XD/6-311++G**級別下得到的,結構是在這個級別下對陰離子優化得到的,計算時用Gaussian 16默認的IEFPCM模型表現了水環境。相關的Gaussian輸入輸出文件和fchk文件都可以在http://www.shanxitv.org/attach/658/file.rar下載。
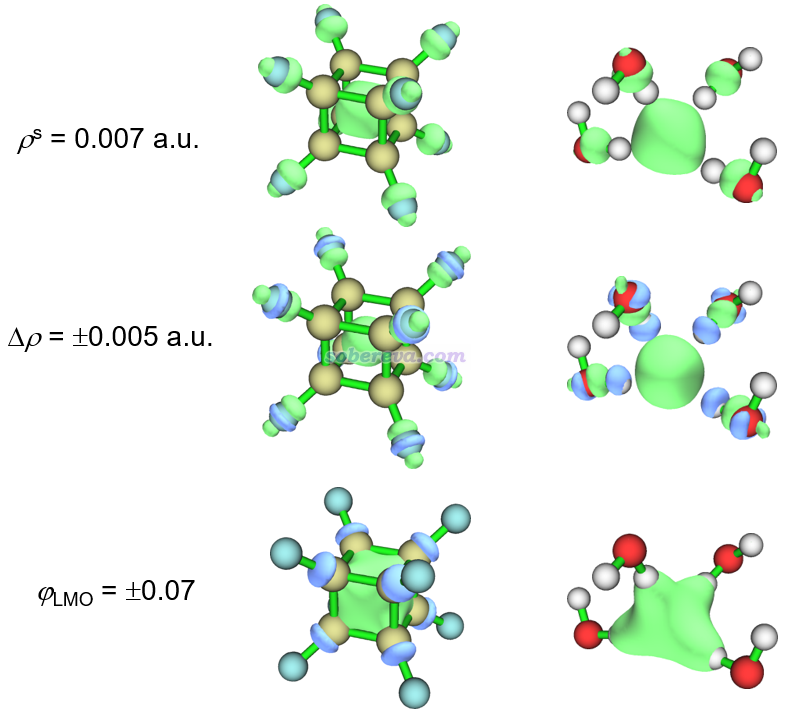
由上可見,三種不同方式給出的圖像雖然不同,但共性都很明顯,即體系中央有一坨顯著的電子分布,體現了過剩電子的存在。但過剩電子并不是100%完全定域在體系最中央的,由圖可見在其它部分也有一定程度的離域。
之所以以上兩個體系的過剩電子比較集中分布在中央,是因為體系中央區域的靜電勢相對更正,對額外加入的電子束縛能力比其它地方更強。具體來說,C8F8體系中每個F-C鍵鍵軸對面區域的碳上有個sigma-hole區域,體現局部缺電子特征,也因而在相應方向電子對C的核電荷的勢場屏蔽較弱。而體系又有多達8個F-C鍵,自然使得籠中央的靜電勢非常正。除了從靜電勢角度考察外,讀者也可以直接用Multiwfn打開文件包里的C8F8.fchk(中性的C8F8)然后按《使用Multiwfn觀看分子軌道》(http://www.shanxitv.org/269)說的去看LUMO軌道,會發現LUMO的分布主體也是籠中央區域,這體現出如果忽略軌道弛豫效應,外來一個電子的話必定主要分布在籠中央。(H2O)4外來一個電子后傾向于分布在四個水中央也是類似的原因。其當前結構下四個水都有氫朝向體系中央,水分子里的氫是帶明顯正電荷的,四個水朝著同一個方向時自然會令相應區域靜電勢很正、容易被外來電子優先占據。
2 過剩電子的回轉半徑
為了定量描述過剩電子的分布廣度,特別是其束縛在受限環境中的情況,很多文章都使用回轉半徑(radius of gyration)這個指標。回轉半徑越大,過剩電子分布得越彌散。對上述各種描述過剩電子的實空間函數都可以按照本節說的方式計算函數的回轉半徑,并將其視為過剩電子的回轉半徑用于定量討論。
對于一個三維實空間函數f,它的分布中心定義如下
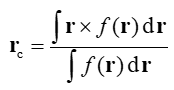
下面的3*3矩陣叫做函數的二階矩,其中x,y,z是積分坐標相對于函數分布中心的坐標的三個分量
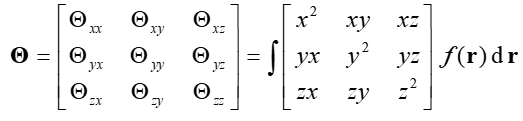
然后利用二階矩的本征值ε1、ε2、ε3就可以計算回轉半徑了:
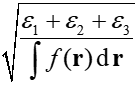
<r^2>也是展現函數分布廣度的一個常用的量,筆者在《電子空間范圍<r^2>和電子徑向分布函數的含義以及在Multiwfn中的計算》(http://www.shanxitv.org/616)中有專門的介紹。<r^2>就是二階矩的三個對角元簡單的加和而已,對應于回轉半徑公式里的分子項。
如果f是有正有負的函數,而且正負部分積分值的數量級相仿佛,上面各式中的f最好取其絕對值來計算,從而避免正負抵消造成的影響。如果不取絕對值有時候還會使得結果毫無意義,比如考察單重態雙自由基體系的自旋密度,正負部分積分會正好抵消,回轉半徑的分母就為0了,根本沒法計算中心位置。
3 基于自旋密度計算過剩電子回轉半徑的例子
這里以前面說的水合電子體系為例,演示用Multiwfn基于自旋密度計算其過剩電子的回轉半徑。本文用的Multiwfn是2023-Jan-30更新的3.8(dev)版,更老的版本與本文情況存在一定不符。
啟動Multiwfn,然后輸入
file\H8O4-.fchk
200 //主功能200
11 //計算函數中心、一階、二階矩和回轉半徑。此功能使用的是Becke多中心格點積分方法,默認設置下精度就已經很高了
3 //選擇被考察的函數
5 //自旋密度
2 //計算函數中心
從屏幕上可看到函數的積分值和中心位置。
Integral of the function: 9.99842011E-01 a.u.
Center of the function:
X= -0.09360685 Y= 0.03381961 Z= -0.47523227 Angstrom
然后輸入y,將這個中心當做之后算各種量所用的參考中心位置。之后選1計算各種量,從屏幕上可見回轉半徑的數值:
Radius of gyration: 4.29967591E+00 Bohr 2.27529051E+00 Angstrom
2.275埃這個值和水合電子研究文獻(如J. Phys. Chem. Lett., 8, 2055 (2017))里普遍報道的值是差不多的。定量上肯定有一定差異,不同文章給出的值也都有出入,這和體系模型、計算級別、對過剩電子回轉半徑的定義等方面都有關。
4 基于軌道概率密度計算過剩電子回轉半徑的例子
當過剩電子幾乎能恰好被一個軌道描述時,從軌道概率分布的角度也可以考察過剩電子分布。前面舉例的C8F8-和水合電子體系,用UKS方式計算后其alpha的HOMO軌道分布正好就比較充分體現了過剩電子分布,其0.05等值面圖如下所示
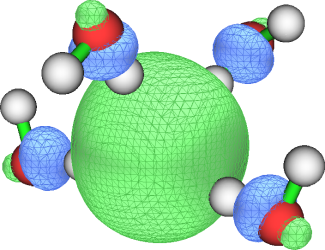
這種情況可以對這個軌道的概率密度計算回轉半徑,并作為過剩電子的回轉半徑,下面就用水合電子舉個例子。注意用alpha-HOMO考察過剩電子的做法不總是普適的,用Multiwfn做軌道定域化或者雙正交化得到的軌道考察過剩電子更為嚴格。
啟動Multiwfn,然后輸入
file\H8O4-.fchk
6 //修改波函數
26 //修改軌道占據數
0 //選擇所有軌道
0 //占據數設為0
21 //alpha-HOMO軌道的序號(進入Multiwfn主功能0的時候在文本窗口就會告訴你HOMO的序號)
1 //電子數設為1。此時總電子密度就正好對應于alpha-HOMO的概率密度了
q //返回
-1 //回到主菜單
200 //主功能200
11 //計算函數中心、一階、二階矩和回轉半徑
2 //計算函數中心。默認的函數就是總電子密度
y //將算出來的中心坐標作為后續計算的參考中心
1 //計算各種量
此時得到的回轉半徑為
Radius of gyration: 4.28690202E+00 Bohr 2.26853086E+00 Angstrom
可見和之前基于自旋密度得到的回轉半徑幾乎完全一致,也體現出這兩種做法對此體系都是得當的。
5 基于密度差計算過剩電子回轉半徑的例子
這一節通過本文第一張圖里的密度差(Δρ)的分布計算水合電子體系過剩電子的回轉半徑。這個方法步驟最多,但相對來說最為普適。比如體系原本是一個二重態體系,額外來了一個電子后變成閉殼層狀態,要用回轉半徑考察額外電子的分布顯然就不能基于自旋密度來算了(處處為0),而可以基于陰離子態與中性狀態的密度差來算。
先把Multiwfn目錄下的settings.ini里的iuserfunc設為-1,此時用戶自定義函數(user-defined function)將對應于格點數據插值產生的函數。之后計算密度差格點數據,啟動Multiwfn,然后輸入
file\H8O4-.fchk
5 //計算格點數據
0 //自定義運算
1 //有一個文件將要與當前體系相運算
-,file\H8O4.fchk //讓當前波函數的屬性減去H8O4.fchk記錄的中性波函數的屬性
1 //屬性是電子密度
3 //高質量格點
此時可以看到如下所示的當前格點數據的積分值,包括所有值、正值部分、負值部分的積分。
Summing up all value and multiply differential element:
0.997642151563456
Summing up positive value and multiply differential element:
1.17292565123273
Summing up negative value and multiply differential element:
-0.175283499669268
總積分值越接近陰離子與中性狀態電子數的差值1.0說明格點數據越理想。當前的偏差很小,就算可以接受了。還可以看到密度差數據的負值部分積分值-0.175沒小到可以忽略,因此之后基于密度差來得到函數的分布中心、回轉半徑時應當對函數的絕對值進行計算,避免正負部分抵消的影響。
注意對于更大的體系,建議自己手動輸入格點間距以確保格點間距足夠小,否則之后的回轉半徑計算不準確,詳見《Multiwfn FAQ》(http://www.shanxitv.org/452)的Q39。
現在密度差格點數據就已經在內存里了。接著輸入
0 //返回主菜單
200 //主功能200
11 //計算函數中心、一階、二階矩和回轉半徑
3 //選擇被考察的函數
100 //用戶自定義函數
5 //基于函數的絕對值來計算函數中心
y //將算出來的中心坐標作為后續計算的參考中心
-1 //之后計算各種統計量的時候用函數的絕對值代替原本函數值
1 //計算各種量
結果如下
Radius of gyration: 4.80321486E+00 Bohr 2.54175184E+00 Angstrom
這個方法得到的回轉半徑比前面基于自旋密度和軌道概率密度得到的稍大,也是合理數值。
本節基于格點數據插值作為被考察的函數的方式也可以用于其它格點數據。比如某個計算程序無法產生被Multiwfn支持的波函數文件,但是直接給你了記錄xxx函數的格點數據的cub文件(或其它Multiwfn支持的格點數據格式,如.dx、.grd、CHGCAR等),也同樣可以先把iuserfunc設為-1,然后載入這個cub文件使里面的格點數據讀到內存里,之后跳過本節產生格點數據的過程,直接進入主功能200做后續的分布特征的計算。
6 總結&其它
本文通過圖形方式結合兩個簡單體系介紹了過剩電子的概念,并著重介紹了怎么利用Multiwfn基于不同函數計算回轉半徑,用來衡量過剩電子的分布廣度。本文的例子也充分體現了Multiwfn在設計上的靈活性。
很多文章都通過從頭算分子動力學考察含有過剩電子體系的動態行為(PS:北京科音的CP2K培訓班里就有液態水中水合電子形成過程的動力學模擬例子),并分析過剩電子回轉半徑隨時間的變化,以及回轉半徑數值的分布情況。實現這種目的只要把本文的內容與《詳談Multiwfn的命令行方式運行和批量運行的方法》(http://www.shanxitv.org/612)里說的相結合就可以輕易做到。具體來說,比如ORCA和CP2K做從頭算動力學可以每隔一定幀數產生一個molden文件,動力學跑完之后,自己寫個腳本調用Multiwfn依次處理各個molden文件,用grep、awk之類的命令自動提取數據,就OK了。http://www.shanxitv.org/612里都給了現成的對整條軌跡做波函數分析的例子,稍微改改就能實現自己的目的。
本文舉例的過剩電子束縛在陰離子體系籠狀區域中央僅僅是含有過剩電子體系的一類,過剩電子還可以以其它形式出現。比如堿、超堿原子的電離能非常小、很容易轉移走,將它們摻雜進中性體系往往可以給原體系引入被束縛較弱的過剩電子,并給體系帶來顯著的非線性光學特征,可以看J. Comput. Chem., 38, 1574 (2017) DOI: 10.1002/jcc.24796中的相關討論。