電子空間范圍<r^2>和電子徑向分布函數的含義以及在Multiwfn中的計算

電子空間范圍<r^2>和電子徑向分布函數的含義以及在Multiwfn中的計算

First release: 2021-Sep-7 Last update: 2021-Sep-8

0 前言

偶爾有人問我Gaussian程序算完了之后，輸出文件中Electronic spatial extent (au): <R**2>后面的值是什么意思，以及筆者的Multiwfn程序能不能算這個。在這里我就寫個文章專門說一下。Electronic spatial extent可以翻譯為“電子空間范圍”，可以表示為<r^2>（**和^都代表取多少次方，本文統一用^符號）。電子密度的徑向分布函數（radial distribution function, RDF）和<r^2>有密切聯系，借助它可以將不同區域對<r^2>的貢獻圖形化展現，便于更深層次了解不同體系<r^2>大小的差異，因此一起在此文說一下。<r^2>實際上也可以對電子密度以外的函數進行計算來考察其空間分布廣度，在本文最后會提及。

<r^2>和回轉半徑有密切聯系，對于后者我結合過剩電子體系另寫了一篇文章做了專門介紹：《使用Multiwfn展現過剩電子（excess electron）并計算它的回轉半徑》（http://www.shanxitv.org/658）。

讀者請務必使用2021-Sep-8及之后更新的Multiwfn，否則和本文很多敘述情況不符。

1 <r^2>的定義

<r^2>的計算公式如下

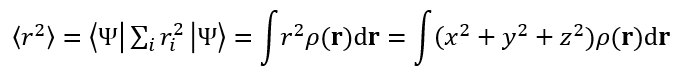
Ψ是體系的電子波函數，i是電子序號，尖括號是Dirac符號。斜體r是指的電子坐標與原點(0,0,0)間的距離，有r^2=x^2+y^2+z^2，這里x、y、z是電子坐標矢量（粗體r）的三個笛卡爾分量。<r^2>顯然就是體系波函數的r^2算符的期望值，等同于電子密度ρ乘上相應位置的r^2在全空間進行積分。

根據計算公式可明顯看出，當體系的總電子數恒定時，電子整體分布偏離原點越多，或者說空間分布范圍越廣闊，則<r^2>會越大，這是為什么<r^2>被稱為“電子空間范圍”。利用<r^2>的這個特點，可以對比不同體系或者同一體系不同狀態下的電子整體分布的廣度或彌散程度。當然了，<r^2>這個指標定義非常簡單，有其局限性，要注意根據其計算形式正確理解其物理意義，不能在不適合使用的時候濫用它來瞎討論。

2 <r^2>的計算

Gaussian計算完畢后直接就給出了<r^2>。Multiwfn的主功能300的子功能5里也能直接輸出<r^2>，結果和Gaussian是完全相同的。使用Multiwfn的好處之一在于Multiwfn支持幾乎所有主流量子化學程序產生的波函數信息做計算，詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379），因此如果你是Gaussian以外的量子化學程序的用戶也都可以方便地靠Multiwfn計算<r^2>。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載，相關入門知識見《Multiwfn入門tips》（http://www.shanxitv.org/167）和《Multiwfn FAQ》（http://www.shanxitv.org/452）。

下面舉個例子，使用Multiwfn分別計算He的基態和第一激發態的<r^2>，看看有什么不同。這里通過Gaussian 16在wB97XD/aug-cc-pVTZ級別下產生波函數文件。涉及的文件都可以在http://www.shanxitv.org/attach/616/file.zip下載。

先計算基態的He，使用的Gaussian輸入文件He_GS.gjf內容如下
%chk=C:\He_GS.chk
# wb97XD/aug-cc-pVTZ
[空行]
He atom
[空行]
0 1
He 注：就一個原子，不用寫坐標。此原子會在(0,0,0)位置

計算完畢后就有了He_GS.chk。用formchk將之轉成He_GS.fch。啟動Multiwfn，載入此文件，然后輸入
300 //其它功能（Part 3）
5 //計算偶極矩、多極矩和電子空間范圍
程序先輸出偶極矩、四極矩、八極矩、十六極矩，然后在末尾看到了<r^2>
Electronic spatial extent <r^2>: 2.428668
Components of <r^2>: X= 0.809556 Y= 0.809556 Z= 0.809556
這里<r^2>是用的原子單位，所以寫到文章里就寫2.43 a.u.即可。由于He的電子密度是球對稱分布的，因此<r^2>的三個笛卡爾分量數值是相同的，它們的加和就是<r^2>。

再來算一下S1激發態的<r^2>。使用的Gaussian輸入文件如下（如果是G09 C.01之前的版本還需要寫上density關鍵詞）。這里使用TDDFT進行計算，寫TD默認是root=1，故第一激發態（S1）的波函數對應的自然軌道會被產生并寫入到輸入文件末尾指定的C:\He_S1.wfn文件里。更多相關細節見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。
# wb97XD/aug-cc-pVTZ out=wfn TD
[空行]
He atom
[空行]
0 1
He
[空行]
[空行]
C:\He_S1.wfn

把He_S1.wfn載入Multiwfn，還是進入主功能300的子功能5，得到的結果如下
Electronic spatial extent <r^2>: 20.472770

可見這個值遠比基態的2.43大得多得多！說明He的S1態的電子分布遠比基態要彌散得多。為什么會這樣？可以用Multiwfn打開激發態計算的Gaussian輸出文件，按照《使用Multiwfn便利地查看所有激發態中的主要軌道躍遷貢獻》（http://www.shanxitv.org/529）里的做法看一下S0->S1激發的軌道貢獻，顯示的是
# 1 18.7170 eV 66.24 nm f= 0.00000 Spin multiplicity= 1:
H -> L 100.0%
可見S0->S1激發完全由HOMO->LUMO躍遷所貢獻，因此看一下這兩個軌道圖形就可以知曉電子是怎么激發的。按照《使用Multiwfn觀看分子軌道》（http://www.shanxitv.org/269）所述，用Multiwfn打開He_GS.fch，在主功能0里看到的HOMO和LUMO圖像如下，等值面數值用0.03 a.u.，用points風格顯示（記得選擇保存圖片文件，比直接在圖形窗口里看到的圖像效果好得多）

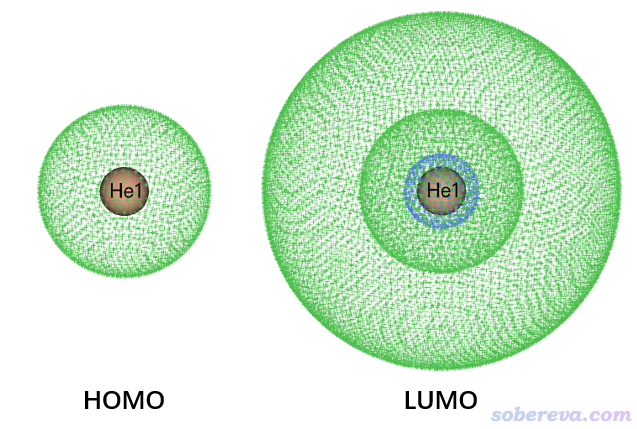
明顯HOMO是He的1s軌道，LUMO是He的2s軌道，因為這倆都是球對稱的，而且LUMO比HOMO分布廣闊得多。由于S0->S1是1s->2s原子軌道的躍遷，必然S1的<r^2>遠大于S0的。

實際上，不用<r^2>也可以說明S1態電子分布更廣。例如Bader將電子密度0.001 a.u.定義為氣相的范德華表面，里面包圍的范圍作為范德華體積，用Multiwfn以這種定義算范德華表面積和體積也能夠說明問題，具體做法在《談談分子體積的計算》（http://www.shanxitv.org/102）里第3節說了。使用He_GS.fch算的基態的表面積是9.87 ?^2，體積是66.58 Bohr^3。而使用He_S1.wfn計算的激發態的表面積是54.31 ?^2，體積是366.50 Bohr^3。由此也充分體現出He激發態的電子密度分布比基態廣闊得多。

Multiwfn還可以對某個軌道的概率密度來計算其<r^2>以衡量其彌散程度，即前述<r^2>計算公式里的ρ不是體系的總電子密度而是特定軌道的概率密度。例如，我們要對S0_GS.fch里記錄的HOMO（即1s軌道）分計算其<r^2>，在Multiwfn載入S0_GS.fch后，輸入：
6 //修改波函數
26 //修改軌道占據數
0 //選擇所有軌道
0 //占據數清零
1 //選擇1號軌道（對應HOMO）
1 //占據數設1.0
q //返回
-1 //返回主界面
300 //其它功能（Part 3）
5 //計算偶極矩、多極矩和電子空間范圍
此時得到的<r^2>為1.214 a.u.。之后若要再計算LUMO軌道的<r^2>，就返回主界面，重新做一遍上述操作，但是改為把2號軌道（對應LUMO）占據數設1.0，最后得到的<r^2>為20.343 a.u.。這直接體現出2s軌道遠比1s空間分布范圍要大。

值得一提的是，由于體系的總密度可以寫為各個占據軌道密度的加和，因此<r^2>也可以精確分解為所有占據軌道貢獻的加和。利用主功能26的子功能6，把其它軌道占據數都設成0，算出來的<r^2>就是這個軌道對<r^2>的貢獻。若大家想一次性把所有軌道對<r^2>的貢獻都分別得到，自己寫個簡單的shell腳本就可以輕易實現，參考《詳談Multiwfn的命令行方式運行和批量運行的方法》（http://www.shanxitv.org/612）。

在《使用Multiwfn繪制原子軌道圖形、研究原子殼層結構及相對論效應的影響》（http://www.shanxitv.org/152）中筆者專門說過，相對論效應可能明顯影響原子軌道的徑向分布，大家感興趣的話可以也考察一下相對論效應是如何影響原子軌道的<r^2>的。

這一節的例子只是算一個原子，計算分子的<r^2>的過程是完全相同的。需要提醒的是，為了讓<r^2>有意義，計算前通常應當讓分子的中心在原點位置。如果是Gaussian用戶，Gaussian計算時自動就會把體系擺到標準朝向下，此時體系的核電荷中心就在原點位置，這是得當的。如果你用的量子化學程序不會自動這樣做，可以用《Multiwfn中非常實用的幾何操作和坐標變換功能介紹》（http://www.shanxitv.org/610）文中介紹的相應功能讓幾何優化過的體系的核電荷中心處在坐標原點，之后再做個單點計算得到算<r^2>用的波函數文件。

當電子密度分布偏離球對稱特別明顯的時候，即各向異性比較強的時候，對不同方向區分討論是很重要的。比如用Multiwfn計算18碳環cyclo[18]carbon（相關研究見http://www.shanxitv.org/carbon_ring.html）的電子密度的<r^2>，會發現平行于環的方向數值達到約2700，而垂直于環的方向數值僅有73.4，充分體現出在平行于環的方向電子分布延展廣度遠遠大于垂直于環的方向。

3 <r^2>與分子特征、性質的相關性

<r^2>與體系的一些特征、性質有一定相關性，在一些論文里做了些討論，這里簡單提一下。

J. Mol. Struct.: THEOCHEM, 728, 231 (2005)里專門研究了水合鎂離子的特征，考慮了1~9個水與Mg2+配位的情況，1~8個水配位的優化后的結構如下

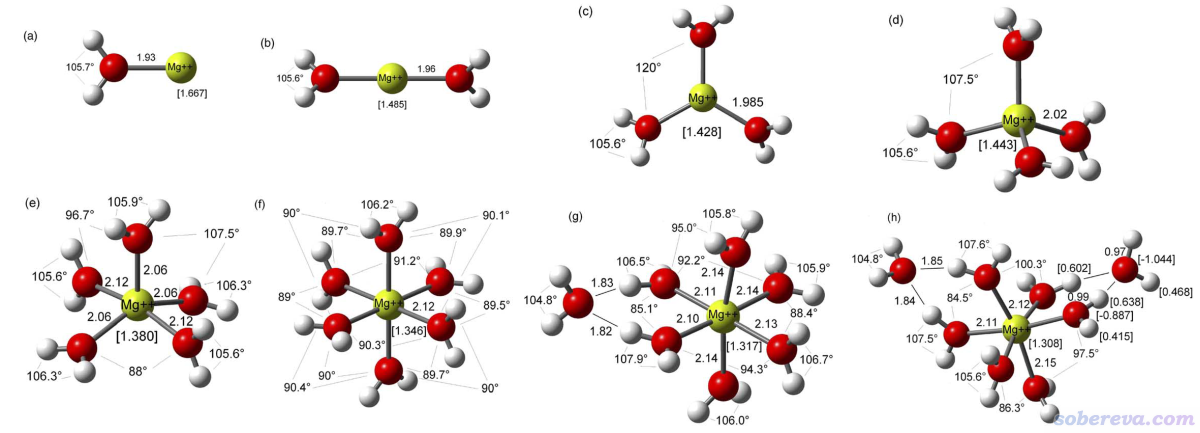
文中對每個結構都計算了<r^2>和各項同性極化率<α>，并繪制了<r^2>^(3/2)與<α>的關系圖，如下所示

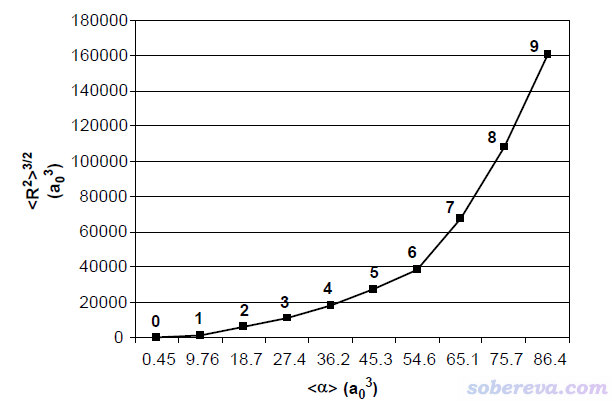
隨著配位層的水的數目增多，電子在越廣的地方有分布，自然<r^2>會逐漸增大，上圖看到的情況完全是理所當然。并且由于有更多的電子可以響應外電場，因此上圖所示的極化率隨著配位水增加數逐漸增大也是必然的。<r^2>和<α>間的正相關性是比較普遍的現象。

在Chem. Phys. Lett., 454, 323 (2008)中，作者對氮取代的并苯的不同類型的結構做了計算，包括Mobius環、普通環狀和線型

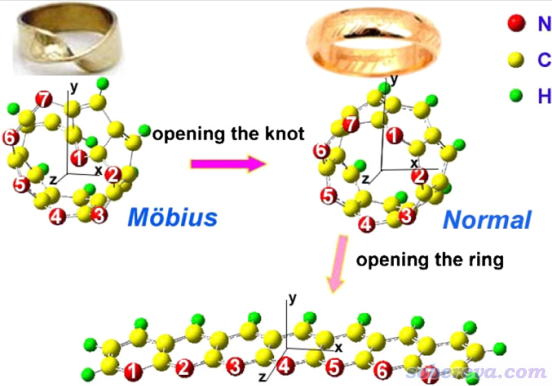
對上面三個體系計算的<r^2>和靜態第一超極化率β0如下所示

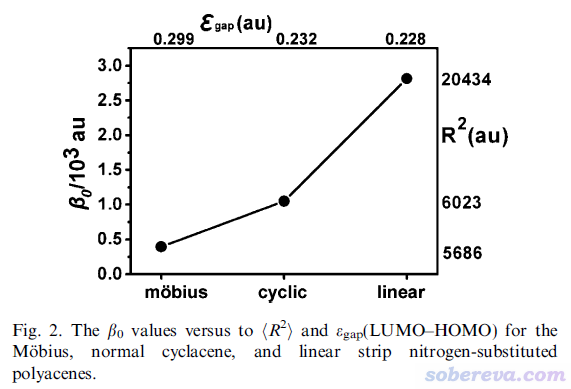
如上可見<r^2>和第一超極化率大小都是線型>普通環狀>Mobius環。線型結構是此體系最延展的狀態，自然電子分布范圍最大，而普通環狀和Mobius環的電子分布范圍的差異不大，由上圖可見二者分別為6023和5686，因此只有借助實際計算的<r^2>才容易定量區分大小。上圖體現出<r^2>與第一超極化率往往也有不錯的正相關性，在理論研究相似結構的非線性光學特征差異的時候可以順帶關注一下<r^2>。

SN Appl. Sci., 2, 418 (2020)中作者研究了一系列多氯聯苯以及帶有取代基的情況，研究中對兩個苯環間的二面角進行了掃描并計算了各個結構的第一超極化率和<r^2>，如下圖所示。可見第一超極化率和<r^2>有正相關性，再次體現出<r^2>與非線性光學性質之間的緊密聯系。

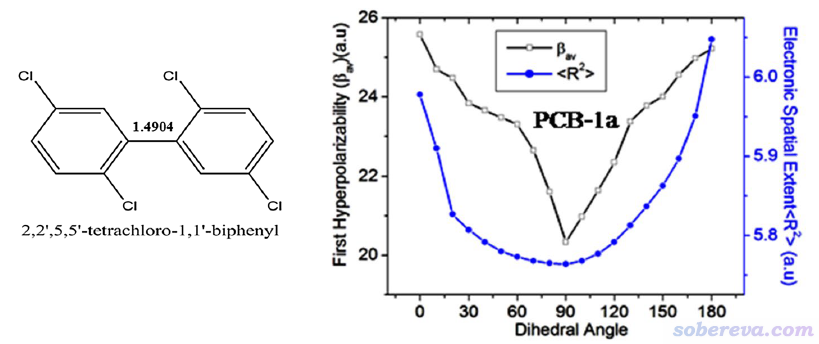
Electrochimica Acta, 115, 234 (2014)的作者將<r^2>視為是離子的電子密度體積的一種衡量，計算了電解液中不同離子的<r^2>，并基于此討論了納米多孔電極充電和放電過程的過電勢問題。

4 電子密度的徑向分布函數

某個三維函數f的徑向分布函數定義如下。r的含義同前，是距離原點的徑向坐標，Ω是球極坐標。注意對RDF從r=0積分到r=∞相當于對f進行整個三維空間的積分。

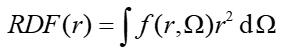
<r^2>與電子密度的RDF之間有如下關系

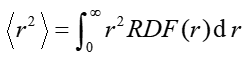
因此，如果你想了解位于不同徑向距離的電子對<r^2>的貢獻，以及分析不同體系或不同狀態間<r^2>差異的來源，可以考察r^2*RDF的曲線圖。Multiwfn程序直接提供了繪制和導出任意函數的RDF曲線的功能，大家自行把它再乘上r^2即可。

我們這里繪制一下He的基態的r^2*RDF曲線圖。啟動Multiwfn，載入He_GS.fch，然后輸入
200 //其它功能（Part 2）
5 //對指定的實空間函數繪制RDF
0 //計算RDF和積分曲線
現在可以選0觀看RDF曲線圖，但我們目前想考察的是r^2*RDF，因此選5把RDF曲線數據導出為RDF.txt，其中第二列是以埃為單位的徑向距離，第三列是RDF數值（a.u.）。之后把RDF.txt導入到比如Origin里，新增加一列D，令其內容為RDF那一列數值乘上徑向距離那一列除以0.5291772（變為Bohr為單位）之后的平方，如下所示

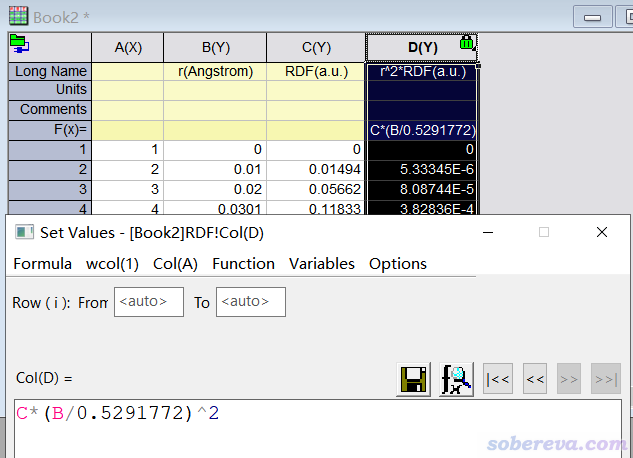
之后將徑向距離（B列）和r^2*RDF（D列）分別作為橫坐標和縱坐標即可繪制展現不同徑向距離對<r^2>貢獻的曲線圖。以He_S1.wfn為輸入文件，也以同樣方式獲得He的S1態的r^2*RDF(r)曲線數據。下圖將S0態和S1態的r^2*RDF曲線繪制在了一起

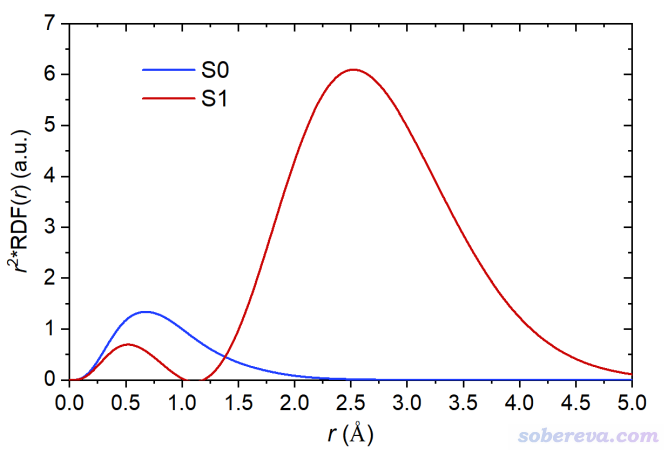
上圖曲線下方的積分面積就相當于<r^2>。由于S0態兩個電子都在彌散程度很低的1s軌道上，只有距離原子核不太遠的區域對<r^2>有貢獻。S1態的一個1s電子被激發到了2s上，導致圖中出現了兩個峰。由于2s上的電子主要分布區域的r較大，導致外側的峰的面積特別大，即對<r^2>的貢獻極大。這也體現出<r^2>的數值極度凸顯出分布范圍較廣的電子的存在感。

5 對其它函數考察<r^2>衡量分布范圍

實際上，對其它實空間函數也可以計算<r^2>來定量體現它的空間分布廣度。在非常靈活的Multiwfn中可以對任意實空間函數計算<r^2>，相當于把前文的<r^2>公式里的電子密度改為相應的函數。這需要用到Multiwfn主功能200的子功能11，這個功能可以對任意Multiwfn支持的實空間函數計算表征其定量分布的指標，也包括<r^2>，詳情見Multiwfn手冊的3.200.11節。
注：用這個功能算電子密度的<r^2>也完全可以，只不過這個功能是用的多中心數值格點積分算法來做的，而前文的功能是基于解析積分做的，故這個功能對大體系耗時明顯更高，而且精度會稍微低一丁點，所以算電子密度的<r^2>沒必要用這個功能。

下面就舉個例子，對[(H2O)4]-水合電子體系計算自旋密度的<r^2>來展現此體系中那個未配對的電子分布的廣度。在wB97XD/6-311++G**級別結合IEFPCM模型表現水環境的情況下優化的無虛頻的[(H2O)4]-結構的波函數文件是http://www.shanxitv.org/attach/616/file.zip里面的H8O4-.fchk。對它按照《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》（http://www.shanxitv.org/353）的做法繪制的自旋密度=0.005 a.u.的等值面圖如下，可見水合電子主要是被四個水圍在中間（但也有部分離域到氧上了），而且四個氫朝著被溶劑化的電子方向形成O-H...e-氫鍵。

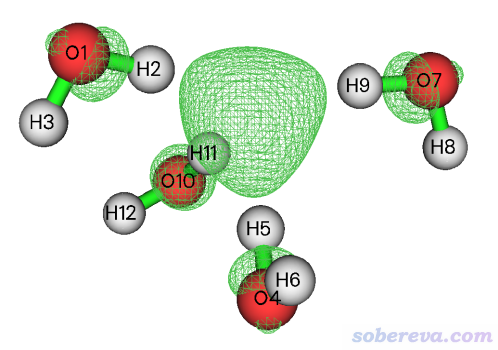
現在來計算這個自旋密度的<r^2>。啟動Multiwfn，載入H8O4-.fchk，然后輸入
200 //其它功能（Part 2）
11 //計算一個實空間函數的中心、一階矩、二階矩、回轉半徑和<r^2>
3 //選擇被考察的函數（默認是電子密度）
5 //自旋密度
2 //計算函數的中心位置。然后屏幕上就輸出了中心位置
y //將這中心位置當做接下來計算各種表征函數分布的量的原點位置
1 //對選定的函數計算各種表征分布的量

輸出信息如下
Integral over whole space: 9.99955676E-01 //此為自旋密度的全空間積分

The first moment:
X= 8.42381720E-15 Y= 9.87404603E-15 Z= 6.21724894E-15
Norm= 2.07111665E-28

The second moment:
XX= 6.74642468E+00   XY= 6.02776286E-02   XZ= 3.72437358E-02
YX= 6.02776286E-02   YY= 5.92056938E+00   YZ= -2.95383533E-02
ZX= 3.72437358E-02   ZY= -2.95383533E-02   ZZ= 5.80589584E+00
Eigenvalues: 5.79600793E+00 5.92478407E+00 6.75209791E+00
Sum of eigenvalues (trace of the second moment tensor): 1.84728899E+01
Anisotropy: 8.91701906E-01

Radius of gyration: 4.29810525E+00

Spatial extent of the function <r^2>: 18.472890

即自旋密度的<r^2>為18.47 a.u.，實際上它也正好等于二階矩（the second moment）矩陣三個對角元的加和。這三個對角元可以分別用來考察X、Y、Z方向各自對<r^2>的貢獻是多大。由于XX（6.75）稍微大于YY（5.92）和ZZ（5.80），說明水合電子在X方向上的延展程度比Y、Z方向略微大一點。

上面輸出的Radius of gyration（回轉半徑）也是衡量函數分布廣度的指標，它相當于<r^2>除以函數的積分值再開根號。由于當前體系自旋密度全空間積分值為1.0，因此上面輸出的回轉半徑4.298就相當于<r^2>直接開根號。

6 計算原子的電子密度的<r^2>

Multiwfn不僅可以計算整個分子的電子密度的<r^2>，還可以計算原子的，由此可以考察化學體系中各個原子上的電子的空間分布的廣度，以更好地理解不同原子的特征。Multiwfn的模糊空間分析（子功能15）可以基于模糊式劃分定義原子空間，盆分析（主功能17）可以基于電子密度零通量面劃分得到AIM理論定義的原子空間，在這兩個主功能里都有相應的選項計算原子空間內的偶極矩、多極矩以及<r^2>，這里用的r不是相對于(0,0,0)的距離，而是相對于被考察的那個原子核的距離。

這里舉個例子，使用Hirshfeld劃分計算氟代乙烷的各個原子的<r^2>。啟動Multiwfn，然后依次輸入
examples\C2H5F.wfn
15 //模糊空間分析
-1 //修改模糊空間定義
3 //Hirshfeld劃分（基于內置球對稱化的原子密度計算）
2 //計算原子和分子的多極矩以及<r^2>
程序依次輸出了各個原子的多極矩和<r^2>（Atomic electronic spatial extent <r^2>后面的值，X/Y/Z分量在下面一行也給了），最后輸出了整個分子的這些量。筆者將各個原子的<r^2>在這里匯總列出，其中1~4號原子是甲基部分，5~7是亞甲基部分：
C1 12.308481
H2 2.250021
H3 2.258035
H4 2.250021
C5 12.038875
H6 2.197460
H7 2.197460
F8 10.077855
可見氫原子的電子分布范圍遠小于重原子的，這和我們對原子半徑的認識也是一致的。C5的<r^2>小于C1的，這可能一定程度上是因為C5連了電負性較大的氟，導致其Hirshfeld原子電荷（在上面計算時一并輸出了）0.116比C1的-0.058更正，也因此帶的電子數更少。F帶的電子數雖然比C更多，但由于F的核電荷更大，電子被束縛得更緊，因此其<r^2>比C1和C5都小（你也可以對孤立的F和C原子進行計算，也是這樣的大小關系）。

7 總結

本文對Gaussian輸出文件里能直接看到的電子空間范圍<r^2>的定義、物理意義，以及一些實際應用都做了介紹，并且結合具體例子講解了如何用Multiwfn來計算<r^2>。從上文可看出，通過Multiwfn考察<r^2>很靈活強大，比靠Gaussian直接來計算有諸多重要好處：(1)不花錢 (2)支持幾乎所有量化程序 (3)可以獲得<r^2>的不同分量（這對于明顯偏離對稱的體系尤其重要）(4)可以計算各個軌道的貢獻來分析其本質 (5)可以借助徑向分布函數洞察<r^2>數值的來源 (6)可以考察各個原子的<r^2>。另外，Multiwfn對于任何實空間函數（無論是Multiwfn直接支持的超過100種函數，還是由其它程序產生并以.cub等格點數據文件記錄的）都可以計算<r^2>從而衡量其空間分布廣度，對于討論許多化學問題大有益處。