談談怎么計算化學體系中“原子的靜電勢”
談談怎么計算化學體系中“原子的靜電勢”
文/Sobereva@北京科音 2022-May-29
0 前言
在網上經常有人問我怎么計算原子的靜電勢。“原子的靜電勢”是一個非常含糊不明的詞。靜電勢是一個三維函數,空間中不同的點有不同的數值,顯然靜電勢不是對原子來說的,而是對具體坐標來說的。但有人就是想計算something like“原子的靜電勢”的量,那怎么算?本文我介紹三種比較有實際意義的基于靜電勢計算的對原子而言的值,讀者可以看看哪種是自己真正想要算的,根據實際情況決定算哪種。本文會舉一些計算例子,用到的Multiwfn可以在主頁http://www.shanxitv.org/multiwfn免費下載,不了解相關常識者建議看《Multiwfn FAQ》(http://www.shanxitv.org/452)和《Multiwfn入門tips》(http://www.shanxitv.org/167)。
如果你對靜電勢都完全不了解,切勿稀里糊涂急于計算,至少要知道靜電勢的定義和基本相關常識,否則都不知道自己到底想得到什么,對算出來數據也都是瞎討論。靜電勢基本相關知識看《靜電勢與平均局部離子化能相關資料合集》(http://bbs.keinsci.com/thread-219-1-1.html)。
1 原子的擬合靜電勢電荷
關于擬合靜電勢電荷,我在《RESP擬合靜電勢電荷的原理以及在Multiwfn中的計算》(http://www.shanxitv.org/441)中已經做了大量介紹,并且提供了許多相關資料和諸多計算實例,讀者仔細一看就能充分了解了。簡單來說,原子電荷是位于原子核位置的點電荷,是一種簡單描述化學體系中電荷分布的方式。擬合靜電勢是一種計算原子電荷的思想,使得基于原子電荷粗略計算出的分子范德華表面附近區域(通過一批擬合點來表示)的靜電勢和基于電子密度以更嚴格的方式算的這些區域的靜電勢盡可能一致。擬合靜電勢電荷有不同的具體實現,比如Merz-Kollman、CHELPG、RESP等,都可以用Multiwfn基于量子化學程序計算產生的波函數文件計算,具體做法看http://www.shanxitv.org/441,本文就不再舉例了。從計算思想可知,某原子的擬合靜電勢電荷的數值直接取決于這原子周圍范德華表面附近的擬合點。在這些點上靜電勢整體越正,這個原子的擬合靜電勢電荷通常就越正,反之就越負。
2 原子局部范德華表面的靜電勢平均值
分子的范德華表面上的靜電勢經常通過作圖來直觀考察,例如《使用Multiwfn+VMD快速地繪制靜電勢著色的分子范德華表面圖和分子間穿透圖》(http://www.shanxitv.org/443)。在這個表面上基于靜電勢算的統計量,比如平均值、方差、最大/最小值等,也有很多實際用處,見比如《使用Multiwfn預測晶體密度、蒸發焓、沸點、溶解自由能等性質》(http://www.shanxitv.org/337)里用到的量和《談談如何衡量分子的極性》(http://www.shanxitv.org/518)中的MPI指數,這些量的具體定義看Multiwfn手冊3.15.1節。分子空間可以劃分成一個個原子空間來研究分子中原子的特征,類似地,筆者曾提出“局部分子表面分析”的思想,把分子范德華表面劃分成一個個原子(或一批原子構成的片段)所屬的區域。通過計算這種“原子局部范德華表面”上靜電勢相關的統計量,就可以了解許多跟原子有關的信息。這種分析方法在Multiwfn程序中可以實現,下面就用給個具體例子。
此例是丙烯醛,結構如下。如圖所示,此體系碳原子有三個,羰基碳、alpha碳、beta碳原子,已知羰基碳最容易受到硬親核試劑進攻而發生反應。此例我們著重看看能否通過這些原子的局部范德華表面上靜電勢平均值的差異來說明這一點。
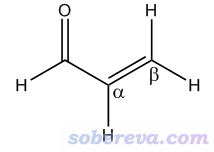
用Multiwfn做局部分子表面分析需要先得到波函數文件,做法見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。在B3LYP/6-31G**級別下通過Gaussian程序產生的此體系的波函數文件已經在Multiwfn文件包里提供了,是examples目錄下的acrolein.wfn。
啟動Multiwfn,然后輸入
examples\acrolein.wfn
12 //定量分子表面分析
0 //開始分析
瞬間就分析完了。默認是以電子密度=0.001 a.u.的等值面定義分子表面(對應于Bader對范德華表面的定義),默認分析的是分子表面上的靜電勢。此功能的相關知識看《使用Multiwfn的定量分子表面分析功能預測反應位點、分析分子間相互作用》(http://www.shanxitv.org/159)。
當前看到一個后處理菜單,選擇選項11 Output surface properties of each atom,然后瞬間就看到了下面這些信息
Note: Minimal and maximal value below are in kcal/mol
Atom# All/Positive/Negative area (Ang^2) Minimal value Maximal value
1 23.00966 0.00000 23.00966 -35.19343001 -0.36509775
2 4.33009 3.67503 0.65506 -5.46462950 11.48235449
3 4.54073 3.06665 1.47409 -1.73335086 7.66399279
4 15.69303 13.78753 1.90549 -17.69011113 19.13728594
5 16.53855 14.76842 1.77013 -20.37979596 16.57402636
6 3.74578 2.94182 0.80396 -1.67072249 10.11939827
7 15.01908 15.01908 0.00000 2.90973611 22.71210240
8 16.73671 16.73671 0.00000 1.14063472 22.64517642
Note: Average and variance below are in kcal/mol and (kcal/mol)^2 respectively
Atom# All/Positive/Negative average All/Positive/Negative variance
1 -24.35460 NaN -24.35460 NaN NaN 72.73909
2 4.65693 5.74623 -1.45429 9.79732 9.01640 0.78092
3 1.30960 2.36409 -0.88412 2.70939 2.46010 0.24929
4 8.37226 10.35882 -6.00183 36.74779 17.22575 19.52204
5 7.07178 8.68115 -6.35535 50.00159 25.34554 24.65605
6 2.21582 3.02333 -0.73900 5.15677 4.95386 0.20291
7 15.34361 15.34361 NaN NaN 22.85750 NaN
8 14.68585 14.68585 NaN NaN 25.92939 NaN
Note: Internal charge separation (Pi) is in kcal/mol, nu = Balance of charges
Atom# Pi nu nu*sigma^2
1 7.134251 NaN NaN
2 3.227929 0.073354 0.718674
3 1.715103 0.083543 0.226349
4 5.171843 0.249024 9.151075
5 5.533206 0.249952 12.498021
6 2.049430 0.037801 0.194929
7 3.976506 NaN NaN
8 4.188833 NaN NaN
以上信息告訴你分子范德華表面上對應各個原子的局部區域中各種基于靜電勢計算的統計值。例如如上All/Positive/Negative area (Ang^2)下面的內容可見,2號原子的局部范德華表面總面積為4.33 ?^2,其中靜電勢為正和為負的面積分別為3.67和0.65 ?^2。再比如,從如上Minimal value Maximal value下面的值可見在2號原子的局部范德華表面中,靜電勢最小和最大值分別為-5.46和11.48 kcal/mol。All/Positive/Negative average下面的值分別是各個原子局部范德華表面上靜電勢平均值、其中靜電勢為正區域的靜電勢平均值、其中靜電勢為負區域的靜電勢平均值。此外還有variance(靜電勢的方差)、Pi指數、nu指數、nu*sigma^2指數,也都是對各個原子局部范德華表面進行的計算,這些指數在Multiwfn手冊3.15.1節都有說明。
當前體系羰基碳、alpha碳、beta碳分別是2、3、6號原子(在Multiwfn載入波函數文件后,進主功能0就可以看到原子序號),由以上信息可見它們局部范德華表面上靜電勢平均值分別為4.656、1.309、2.215 kcal/mol,明顯羰基碳最容易吸引硬堿分子親核進攻它而發生反應。
以上信息中有些量是NaN,代表Not a number,是因為無法計算所致。比如7號H原子局部范德華表面中靜電勢為負區域的靜電勢平均值就是NaN,這是因為它的局部范德華表面上靜電勢全為正,根本不存在靜電勢為負的區域(也體現在了它的靜電勢為負的區域面積為0上)。
還值得一提的是,那些被嚴重包埋的原子是沒有對應的局部范德華表面的。比如C60富勒烯里包夾一個小分子,此時范德華表面完全在C60的外表面上,被包夾的小分子的原子對范德華表面沒有任何貢獻,也因此不可能對這些原子計算局部范德華表面上的信息。對這些原子,Multiwfn在輸出以上信息時是直接略過的。
Multiwfn具體是如何判斷范德華表面各個區域屬于哪個原子的,在Multiwfn手冊3.15.2.2節有說明。如果你想圖形化觀看一下,以人為檢驗范德華表面劃分得是否合理,在選擇完上述的11 Output surface properties of each atom選項后,輸入y,然后Multiwfn就會在當前目錄下輸出locsurf.pdb文件。范德華表面上的各個頂點在此文件里作為碳原子記錄,倒數第二列記錄的B因子信息的數值是相應頂點對應的原子序號。因此,把locsurf.pdb載入VMD程序,根據B因子數值進行著色,就可以通過顏色區分各個原子所屬的局部范德華表面區域了,具體做法看Multiwfn手冊4.12.3節。此例繪制的結果如下。可見此圖淡紅色、肉色和亮紫色小圓點分別是羰基碳、alpha碳和beta碳的局部范德華表面上的頂點,它們的分布很合理,確實能很好地對應相應原子,也因此前面給出的這三個碳的局部范德華表面的靜電勢平均值能合理反映出它們的特征。
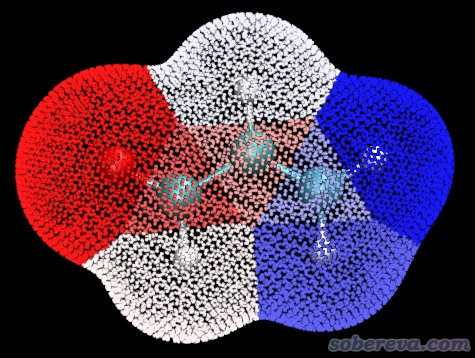
3 原子核位置的靜電勢
對三維空間中各個點都可以計算靜電勢,顯然在原子核位置也可以算,但這樣的位置靜電勢是無窮大的,這從靜電勢計算公式的原子核電荷貢獻部分的數學形式便知。但計算某原子核處靜電勢時把這個原子核對靜電勢的貢獻忽略掉,靜電勢就不是無窮大,而且是有實際意義的。下面說的“原子核處的靜電勢”指的都是這種定義。如果你看到的文獻里討論了原子核處的靜電勢,一般也都是這種定義。
這里著重說一下氫原子的原子核處的靜電勢,實際意義相對較明顯。對于氫來說,原子核處的靜電勢和它作為質子解離的難易程度有密切關系,也即可以用它來對類似物質估計pKa的相對大小。這是因為氫原子核處的靜電勢等同于它的原子核(即一個質子)與體系其它部分的靜電作用能,顯然數值越負,靜電勢吸引作用越強,質子就越不容易解離,pKa就可能越大。需要注意的是,這和這個體系的真空中的質子解離能的負值并不等價,因為實際中質子解離后,陰離子部分的電子結構和幾何結構會發生弛豫,這部分能量變化也會體現在質子解離能里。此外,溶劑效應對不同體系間的pKa的相對大小也有明顯影響。因此,氫核處的靜電勢和相應位點的pKa只有較松散的相關性,只能反映影響pKa因素中的一部分。
作為例子,下面對甲酸、乙酸、乙醇體系的幾個氫來計算原子核處的靜電勢,結構如下
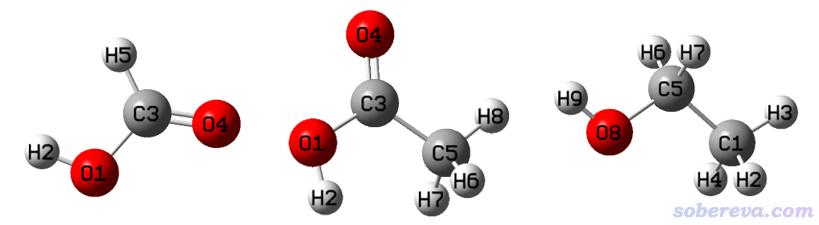
這幾個體系的波函數文件可以在http://www.shanxitv.org/attach/641/file.rar里得到,都是在B3LYP/6-311G**級別下用Gaussian做優化任務時產生的。
先計算甲酸。啟動Multiwfn,輸入
formic_acid.fch
1 //計算一個點的屬性
a2 //計算2號原子的原子核位置的屬性,這個原子是甲酸羧基上的氫
從屏幕上輸出的信息中可找到下面的內容:
Total ESP without contribution from nuclear charge of atom 2:
-0.9477863132E+00 a.u. ( -0.2579058E+02 eV, -0.5947454E+03 kcal/mol)
即曰,這個氫原子核位置的靜電勢(扣除其自身原子核電荷的貢獻)為-0.9478 a.u.,也即在當前幾何和電子結構下,這個氫原子核與體系其它部分的靜電作用能為-0.9478 a.u.。
之后再輸入a5,就得到了甲酸的與碳相連的H5的原子核位置的靜電勢,結果為-1.0628 a.u.。相對于羧基上的H2,顯然這個數值明顯更負,體現出H5原子核被體系束縛得明顯更牢,故更不容易解離掉,這和化學常識一致。
類似地,基于前述文件包里的acetic_acid.fch計算乙酸羧基氫上的原子核處的靜電勢,結果為-0.9589 a.u.。其數值比甲酸的羧基氫的更負,說明這個質子更不容易脫離。這也和水中的pKa的關系一致,乙酸的pKa是4.756,明顯比甲酸的3.745更大。
再用文件包里的ethanol.fch計算乙醇羥基氫的原子核處的靜電勢,結果為-1.0153 a.u.,可見比乙醇的羧基氫負得多得多,這也對應了羥基氫遠沒有羧基氫易于作為質子解離的事實。乙醇在水中的pKa是15.9。
最后,值得一提的是擬合靜電勢電荷和原子局部范德華表面的靜電勢平均值在原理上存在一定正相關性,而原子核處的靜電勢和它們沒密切聯系,除非是原子所處的化學環境類似。