使用Multiwfn計算odd electron density考察激發態單電子分布
使用Multiwfn計算odd electron density考察激發態單電子分布
文/Sobereva@北京科音 2021-Aug-14
1 前言
對于基態是開殼層的體系,比如自由基、過渡金屬配合物等,要考察單電子分布,最常用也是最簡單的做法就是做非限制性開殼層的DFT計算(UKS),然后繪制自旋密度圖,見《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》(http://www.shanxitv.org/353)。UKS也常被用來計算基態是閉殼層體系的最低三重態激發態(T1態),也可以得到其自旋密度。常有人問諸如T2、T3態的單電子分布怎么得到,這些比T1更高的三重態一般沒法直接靠UKS來計算而普遍使用TDDFT來計算。但是Gaussian、ORCA等常用量子化學程序的TDDFT計算并沒法給出激發態的alpha和beta的密度,也相應地沒法獲得激發態的自旋密度來考察單電子分布情況。不過,可以利用Multiwfn將TDDFT計算的激發態密度轉化為odd electron density(OED,可譯為單電子密度函數),通過其圖形可以考察激發態中哪里單電子多哪里單電子少。雖然OED不像自旋密度那樣還能通過正負號體現單電子自旋方向,但一般也足夠討論實際問題。OED是個普適的函數,對于任何能產生密度矩陣的理論方法,比如CASSCF,也都能靠它來考察所得波函數的單電子分布。所以,自旋密度絕對不是考察單電子分布的唯一辦法。
本文將介紹OED的定義,并演示怎么使用Multiwfn計算OED考察TDDFT算的三重態激發態的單電子分布,在Multiwfn手冊4.A.6.1節還有OED的其它用法示例。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載,相關基本常識見《Multiwfn入門tips》
(http://www.shanxitv.org/167)和《Multiwfn FAQ》(http://www.shanxitv.org/452)。讀者請使用2021-Aug-14及以后更新的Multiwfn版本。
2 OED的定義
早在Theor. Chim. Acta (Berl.), 48, 175 (1978), Yamaguchi等人就定義了一種基于密度矩陣的衡量單電子(odd electron)分布的函數。后來Head-Gordon在Chem. Phys. Lett., 372, 508 (2003)的9式定義了更好的衡量單電子數的表達式;基于其思想,Nakano等人在Theor. Chem. Acc., 130, 711 (2011)的2式給出了展現單電子空間分布的實空間函數,即前述的OED函數。
OED基于無自旋自然軌道進行計算,表達式如下
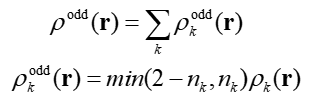
可見OED,即ρ_odd(r),是由各個自然軌道貢獻的,k循環所有自然軌道。min()代表取里面兩個數的最小值,n_k是第k個自然軌道的占據數,ρ_k(r)是k軌道波函數的概率密度。上式min(2-n_k,n_k)體現的是k軌道對應的(有效)單電子數,對應軌道占據數距離閉殼層狀態(0.0或2.0)的差距。其思想容易理解,如果軌道上的電子數n_k<1,則min(2-n_k,n_k)就直接等于n_k,即軌道上的這些電子都算是單電子;如果n_k>=1,則min(2-n_k,n_k)對應的是n_k與2的差值,這部分都當做單電子。
體系的總的(有效)單電子數可以把各個軌道的貢獻加和得到
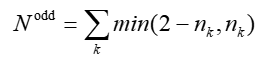
3 例子:BODIPY FL
為了演示如何利用OED展現TDDFT算的激發態的單電子分布,我們用下圖所示的BODIPY FL熒光染料分子作為例子,本例涉及的文件都可以在此下載:http://www.shanxitv.org/attach/583/file.rar。計算都用的是Gaussian 16,計算級別是算激發態常用的PBE0/6-31G*。所有計算用的結構都是S0基態的極小點結構(這沒有什么特殊理由,隨便舉個例子而已)。
首先繪制TDDFT計算的T1波函數的OED,并且也與UKS計算的自旋密度進行對比來檢驗一下OED是否確實能合理展現單電子分布。利用下面的Gaussian輸入文件(本文文件包里的TDDFT_T1.gjf)做TDDFT計算產生T1態的自然軌道,并將之導出為wfn文件
%chk=TDDFT.chk
# PBE1PBE/6-31g(d) TD(triplet) out=wfn
[空行]
b3lyp/6-31g(d) opted
[空行]
0 1
[坐標部分]
[空行]
TDDFT_T1.wfn
算完之后,當前目錄下就有了TDDFT_T1.wfn,里面記錄的是T1態的自然軌道(這是因為當前要求算出來的激發態都是三重態,而且默認的root是1。如果不了解相關知識的話看《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》http://www.shanxitv.org/314)。如果你用的是G09 C.01以前的版本,關鍵詞還需要加上density,否則導出的還是基態的DFT軌道。
作為對照,我們也用UKS算一下T1態,輸入文件如下(本文文件包里的UKS.gjf)
%chk=UKS.chk
# PBE1PBE/6-31g(d)
[空行]
b3lyp/6-31g(d) opted
[空行]
0 3
[坐標部分]
現在來繪制TDDFT的T1態的OED。啟動Multiwfn,載入TDDFT_T1.wfn,然后輸入
6 //修改波函數
26 //修改軌道占據數
0 //選擇所有軌道
odd //將軌道占據數轉化成OED定義的單電子數,即min(2-n_k,n_k)
q //返回
-1 //返回主菜單
由于當前的軌道占據數都已經是相應的(有效)單電子數了,所以接下來對電子密度做任何分析和繪制都等同于對OED來做。這里我們就只用主功能5來繪制一下等值面圖。現在輸入
5 //計算格點數據
1 //電子密度(當前等同于OED)
3 //高質量格點
-1 //觀看等值面
把等值面數值改為0.01 a.u.,就看到了下圖左邊部分。作為對照,將UKS計算產生的UKS.chk用formchk轉化為fch并作為Multiwfn輸入文件,按照《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》(http://www.shanxitv.org/353)所示的過程繪制自旋密度圖,等值面數值也設為0.01 a.u.,如下圖右邊部分所示。
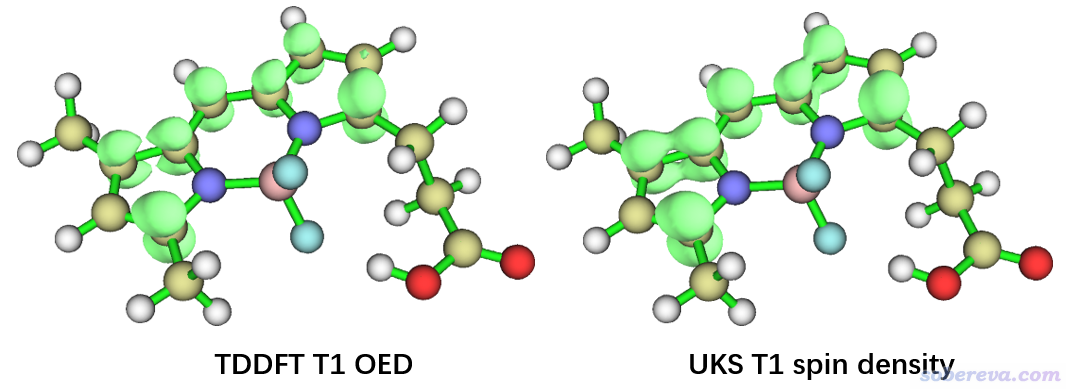
對比可見,兩幅圖并沒顯著差異,這說明基于TDDFT算的三重態激發態波函數繪制的OED可以正確反映單電子分布情況。
下面再繪制一下TDDFT算的T3和S1態的OED圖,在Multiwfn里的操作同前,只不過Gaussian計算用的關鍵詞有所不同,S1用的是# PBE1PBE/6-31g(d) TD out=wfn,T3用的是# PBE1PBE/6-31g(d) TD(triplet,root=3,nstates=5) out=wfn。相應得到的wfn文件TDDFT_S1.wfn和TDDFT_T3.wfn在本文的文件包里也都提供了。OED圖如下所示。
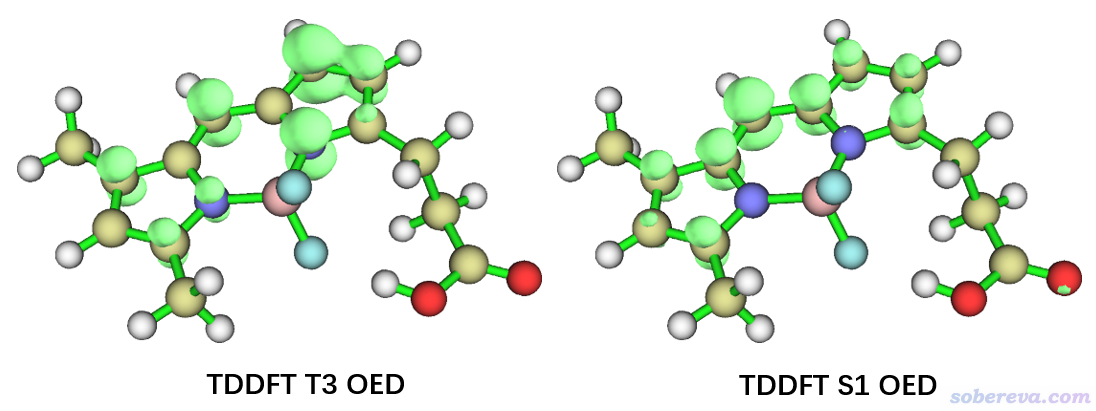
可見T3態的單電子和T1一樣也是分布在共軛平面部分的。S1的OED和前面T1的OED分布頗為相似,這主要也是因為T1和S1的軌道躍遷特征高度相似。從輸出的組態系數來看,T1是
76 -> 77 0.71103
76 <- 77 0.15278
S1是
74 -> 77 -0.15141
76 -> 77 0.69201
76 <- 77 -0.11347
可見二者都是由76 -> 77完全主導的。
值得一提的是,在前述的主功能6的子功能26里輸入odd對占據數進行轉換后,屏幕上會提示所有軌道占據數的加和,比如T1的情況輸出的是
Sum of occupation numbers of selected orbitals: 1.840534
T3的結果是1.988034,S1的結果是1.754538。這些值都很接近2,所以都可以認為差不多有兩個有(效)單電子。
OED的分布還可以做定量考察。比如對T1態的情況,按照前文的過程在使用主功能6將軌道占據數轉化為軌道的(有效)單電子數后,可以輸入以下命令使用Becke劃分計算原子的貢獻
15 //模糊空間分析
1 //對實空間函數在各個原子空間進行積分
1 //電子密度(此時對應OED)
結果如下,顯示了各個原子貢獻值,以及占總值1.840534的百分比
Atomic space Value % of sum % of sum abs
1(C ) 0.17890273 9.720169 9.720169
2(N ) 0.04492675 2.440967 2.440967
3(B ) 0.00539538 0.293143 0.293143
4(N ) 0.04119946 2.238455 2.238455
5(C ) 0.16279675 8.845096 8.845096
6(C ) 0.21869844 11.882355 11.882355
7(C ) 0.16878350 9.170369 9.170369
8(C ) 0.07606307 4.132670 4.132670
9(C ) 0.27330059 14.849007 14.849007
10(C ) 0.26601172 14.452987 14.452987
11(C ) 0.08853443 4.810266 4.810266
...略
這些定量數據和前面的OED等值面圖對應很好,諸如C9、C10的貢獻值最大,確實在前面的T1的OED等值面圖上這倆原子上的等值面是最大的。Multiwfn里也可以改為Hirshfeld或Hirshfeld-I劃分來計算原子的貢獻,用選項1開始計算前先選擇選項-1 Select method for partitioning atomic space修改原子空間劃分方式,按提示操作即可。
讀者如果感興趣的話,還可以看看OED是主要由哪些自然軌道貢獻的。使用主功能6將軌道占據數轉化為軌道的(有效)單電子數后,可以進入主功能0,這是觀看軌道的界面,詳見《使用Multiwfn觀看分子軌道》(http://www.shanxitv.org/269)。在界面左上角選Orbital info. - Show all,然后在文本窗口里會看到各個軌道信息:
[略...]
Orb: 74 Ene(au/eV): 0.000000 0.0000 Occ: 0.004163 Type:A+B
Orb: 75 Ene(au/eV): 0.000000 0.0000 Occ: 0.008586 Type:A+B
Orb: 76 Ene(au/eV): 0.000000 0.0000 Occ: 0.906738 Type:A+B
Orb: 77 Ene(au/eV): 0.000000 0.0000 Occ: 0.907325 Type:A+B
Orb: 78 Ene(au/eV): 0.000000 0.0000 Occ: 0.006671 Type:A+B
Orb: 79 Ene(au/eV): 0.000000 0.0000 Occ: 0.004351 Type:A+B
[略...]
只有那些原先軌道占據數偏離0和2較大的自然軌道,當前對應的(有效)單電子數才較大。如上可見,OED的貢獻主要來自76和77號自然軌道,貢獻分別為0.906738/1.840534*100%=49.26%和0.907325/1.840534*100%=49.30%。它們的0.05等值面的波函數圖形如下
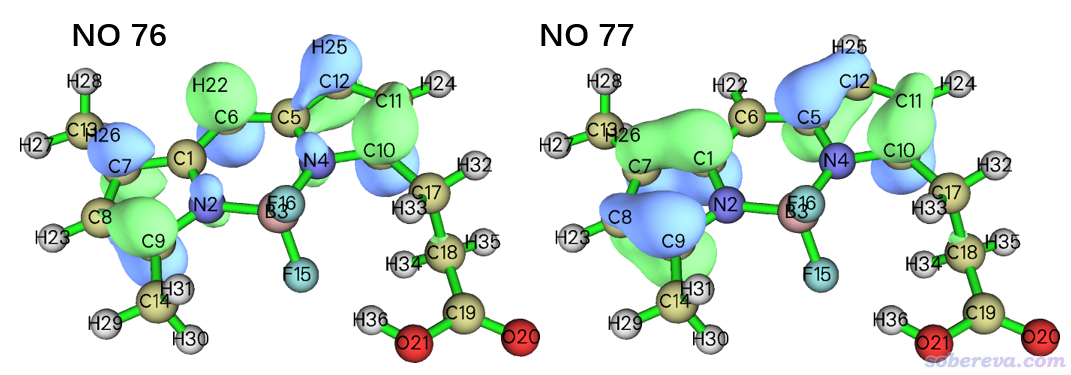
如果將這倆軌道圖和之前的T1的OED等值面圖相對照,會發現OED圖基本上就是這兩個軌道的概率分布的簡單疊加。之前做TDDFT計算時得到的TDDFT.chk里面包含的是基態的分子軌道,如果你用Multiwfn去查看軌道圖形,會發現上面兩個自然軌道的圖形和此體系的HOMO、LUMO幾乎完全一樣,這也是因為如前面的組態系數所看到的,此體系的T1激發幾乎完全是HOMO->LUMO所致,顯然主要貢獻單電子的兩個自然軌道也必然恰好基本就是HOMO和LUMO的形狀。
4 總結
本文介紹了專門用來展現單電子分布的OED的思想,并且通過實例演示了怎么使用Multiwfn非常方便地計算和繪制OED,以及如何考察原子和自然軌道對OED的貢獻。雖然一般大家都是用自旋密度考察單電子分布,確實這也是嚴格的做法,但是很多理論方法在程序實現上或者原理上就是沒法給出自旋密度,而只能給出總密度(以及相應的無自旋自然軌道),此時就只能通過OED來考察單電子如何分布了,凸顯出OED的重要意義。本文示例的TDDFT算激發態只是這種情況之一,還有一個OED特別有用的情況是使用CASSCF計算雙自由基體系的時候,參考比如《CASSCF計算雙自由基以及雙自由基特征的計算》(http://www.shanxitv.org/264),這種情況也沒法獲得自旋密度,因此要考察單電子分布也需要利用OED。過程是先產生記錄CASSCF自然軌道的wfn文件,然后按照本文例子操作即可繪制OED圖。Multiwfn手冊4.A.6.1節專門有個例子演示用OED考察丁烷雙自由基的單電子分布情況,只不過基于的是UKS算的UNO自然軌道,你會發現得到的OED圖和《談談片段組合波函數與自旋極化單重態》(http://www.shanxitv.org/82)一文里的丁烷雙自由基的自旋密度圖幾乎一樣,只不過OED沒有正負號來區分單電子是alpha還是beta。
筆者認為通過OED也可以考察體系哪些地方有較強的電子相關效應,因為軌道占據數偏離整數正是由于電子相關效應所帶來的,見最新版Multiwfn手冊4.A.6.2節的例子。顯然,這要求產生自然軌道的理論方法必須能恰當描述當前體系的電子相關效應才行。OED與Grimme在Angew. Chem. Int. Ed., 54, 1 (2015)和Chem. Eur. J., 23, 6150 (2017)提出的專門圖形化展現靜態相關主要來源FOD (fractional occupation number weighted density)函數的特征頗為相似,只不過FOD利用的是有限溫度DFT計算得到的占據數,這種計算頗為便宜。
用Multiwfn計算OED絕不僅限于使用Gaussian產生的wfn文件作為輸入,只要是用Multiwfn支持的記錄波函數的格式,且里面記錄的是自然軌道就可以。Multiwfn支持的波函數文件格式見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。