亂談外重組能的計算
重組能對Marcus理論計算電子轉移速率很重要,內重組能是大家最關注的,計算方式在此文也談了:《使用Dushin分解重組能和計算Huang-Rhys因子》(http://www.shanxitv.org/330)。外重組能是分子得/失電子或電子態改變后引發環境分子幾何結構弛豫造成的能量變化,其計算關注度低一些,討論其計算方法的文章不多,此文就胡亂對外重組能的計算發表點個人觀點。
和溶液狀態不同的是,晶體狀態下,環境分子沒法自由運動,所以晶體狀態和溶液狀態下計算外重組能的方式差異很大,因此本文分別來談。
1 晶體下外重組能的計算
1.1 基本流程
在分子晶體中發生一次電子/空穴轉移,會令一個分子帶電,同時一個分子回到中性狀態。外重組能可以按下圖這么算,在(1)和(2)->(3)的過程中共優化兩次,共算四個單點。注意有的文章如JPCL,1,941對外重組能的定義是λext(I)和λext(II)的平均值。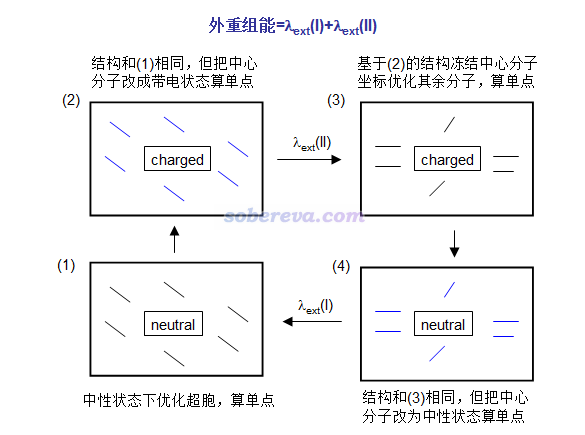
圖中黑色粗框代表分子晶體的晶胞。圖中藍線代表環境分子的電子結構已被中心分子的電荷分布所極化,與此同時中心分子電子結構也被環境分子極化了,但環境分子結構還沒來得及弛豫。
這種方式計算的分子晶體的重組能一般在0.01eV的數量級,見JPCL,1,941和JACS,130,12377的例子(后者主要是講極化能的計算,很靠后部分才牽扯到外重組能)。之所以很小是由于受到晶體環境的束縛,環境分子很不容易發生結構變化。
上圖看起來原理不復雜,但在實際計算時有很多具體問題:
1.2 計算細節
1.2.1 計算模型怎么構建
通常需要先找到分子晶體的cif文件,在此基礎上來創建計算模型。沒有實驗晶體結構就只能通過晶體結構預測程序了。計算一般在PBC下進行。實際計算時絕對不能像上圖中這樣中心分子附近只有幾個環境分子,而是要把素晶胞展成復晶胞,選擇最接近中心處的分子令其電荷發生變化。復晶胞用得越大結果越準確,因為這樣中心分子對附近環境分子的極化效果表現就越真實,同時邊界效應越弱,即邊界分子狀態和bulk狀態越相符。但是復晶胞取大了計算量也猛升,因此要根據分子大小、計算級別、計算姬的性能、程序的選用、對精度的要求等酌情而定。
如果由于程序、方法的限制等原因在PBC下計算不方便,也可以用團簇模型當孤立體系計算,比如下圖這樣。即取一大團分子,在上圖(2)->(3)過程中讓中心分子(紅色)凍結,讓與它最近的一些分子(黃色)允許在優化中弛豫。而最外層的分子(細線表示),在(1)和(2)->(3)的優化中始終保持凍結,以此來表現bulk環境。
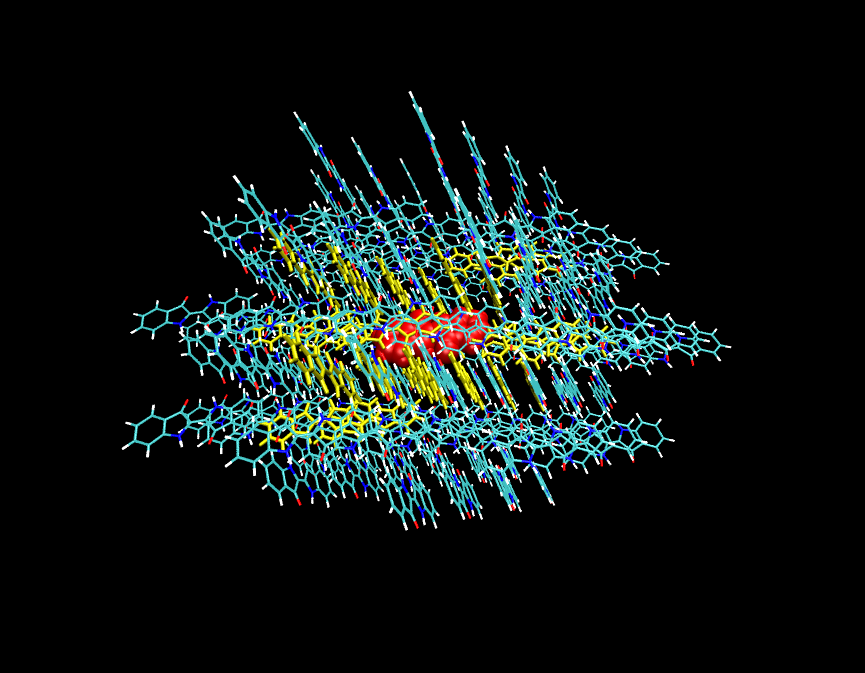
關于復晶胞或團簇應該取的大小,可以參考下面的JPCL,1,941中的一個圖片

1.2.2 用什么理論方法算
量子化學方法來算:量化方式來算外重組無疑精度是最理想的,但很難實現。如果用DFT,優化那么大復晶胞或者團簇太花時間。雖然半經驗或者DFTB容易算得動(尤其是借助MOPAC的MOZYME),但還是有一個關鍵問題是沒法讓指定的電荷只局域在中心分子上而不離域到其它分子。DFT的話,靠CDFT方式雖原理上可以實現,見《談談約束性DFT (CDFT)》(http://www.shanxitv.org/271),但是搞這么大體系太困難,而這種約束方式還沒有程序能對于半經驗來做。另一個可以考慮的做法是用GAMESS-US支持的片段有效勢,把帶指定電荷的中心分子由有效勢來描述,但是可惜這沒法表現環境分子對中心分子電荷的極化(除非再人為加個迭代步驟能讓片段有效勢與環境分子電荷分布自洽,但實現起來很耗時麻煩),而且計算量也同樣巨大。
分子力場來算:
這是最可行的算外重組能的級別,不僅速度足夠快,而且一大好處是便于描述定域的電荷。例如,可以將中心分子的電荷設置為它在帶電狀態下計算出的CHELPG擬合靜電勢電荷,而周圍分子的電荷都設成在不帶電狀態下算出的原子電荷。分子力場也是多種多樣,對于外重組能的計算要從三個方面考慮:
(a)對成鍵項的描述:這關乎到能否優化出合理的結構。UFF之流精度比較爛,用MM2/3、MMFF94之類高精度有機分子力場最理想。不過,由于λext(I)和λext(II)的結構變化過程是相反的,即成鍵項的變化會抵消,因此外重組能計算精度對成鍵項的描述精度敏感性不很高。
(b)對范德華作用的描述:不同力場半斤八兩,不值得一說。
(c)對靜電作用的描述:這是對外重組能計算精度影響最為關鍵的。可極化力場平時用得遠不如固定電荷力場普遍,但計算外重組能時應當盡量用可極化力場,無論是基于浮動電荷方式還是考慮原子極化率都可以。力場的可極化對外重組能的計算之所以這么重要,是因為給中心分子加上一個單位凈電荷后,會強烈對周圍分子電子結構產生極化效果,同時周圍分子也會反過來極化中心分子,這個效應在量化計算時隨著自洽迭代就自然而然體現了,而對于分子力學計算則必須通過可極化力場來表現。在JPCL,1,941中,是基于MM3力場加上可極化項,而點電荷用的是對靜電作用描述較好的CHELPG。在JACS,130,12377中,則是用Gaussian基于B3LYP與UFF結合做電子嵌入的ONIOM(QM:MM),以迭代方式讓QM區域的MK擬合靜電勢電荷與MM區域的QEq電荷達到自洽(具體來說,是先讓QM描述的中心分子的初始電荷設為單獨計算時得到的CHELPG電荷,然后在Gaussian算QEq電荷時固定QM原子的電荷不變去確定MM原子的電荷以表現環境分子對中心分子電荷分布的響應,然后再將MM原子的QEq電荷作為背景電荷來算QM區域的密度分布,進而得到QM原子更新的CHELPG電荷,再反過來計算MM原子的QEq電荷,不斷如此循環以達到QM的CHELPG電荷與MM的QEq電荷間完全自洽,某種意義上類似SCRF自洽反應場的過程。這是通過作者自己額外的代碼實現的,Gaussian本身直接做不了這個QM區電荷與MM的QEq電荷的自洽迭代)。
QM/MM來算:
這個是個很好的算外重組能的做法,對QM與MM區域之間靜電描述比直接用固定電荷的力場準確,如果把QM與可極化力場搞一起就更完美了。前面說的電子嵌入方式的ONIOM(QM:MM)結合電荷自洽過程描述可極化效果也算此類。不過灑家覺得靠QEq雖然可以等效令UFF表現極化效果,但它描述靜電作用的準確度還是不很理想,QEq對靜電勢的描述能力在《原子電荷計算方法的對比》(http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml)中測試過。
1.2.3 用什么程序算
如果以量化方式來算,為了表現電荷定域在中心分子,CDFT的話只有NWChem和Q-Chem可選,如果用片段有效勢只能用GAMESS-US。如果是以分子力學來算,MM3結合額外的可極化設定,或者用AMOEBA可極化力場,無論是當PBC還是團簇來算都可以用Tinker。買了Material studio的人可以用Forcite靠COMPASS來算,不過沒有可極化效果。Gaussian直接用UFF可以按照團簇來算,并且把中心分子的原子電荷固定為擬合靜電勢電荷來確定其余原子的QEq電荷可以粗略表現可極化效果,但必須像JACS那篇文章一樣通過額外方式做迭代才能更充分描述中心分子與環境分子間的相互極化。如果在Gaussian里用電子嵌入的方式做ONIOM(QM:MM)可以把MM原子與QM原子之間的靜電相互作用描述得更準確。Amber自身就能做QM/MM,支持PM6等半經驗和可極化力場,用來算外重組能估計不錯。其它還有很多程序都可以用來前述方式算外重組能,這里就不一一說了。
1.3 關于重組能的拆分
重組能的拆分這一點在大多文獻中說得不夠清楚、確切,這里專門說一下。對于晶體來說,總重組能的計算過程為:
a 優化中性狀態晶胞結構
b 將中心分子設成帶電狀態,對a的結構做單點
c 將中心分子設成帶電狀態,以a的結構為初始結構對晶胞做優化
d 將中心分子還原成中性狀態,對c的結構做單點
然后總重組能=|d-a|+|b-c|。
對上面的流程,如果我們優化時凍結環境分子,得到的就是內重組能;如果優化時凍結中心分子,即1.1節的過程,得到的就是外重組能。注意這樣得到的內重組能和外重組能之和并不是總重組能!因為中心分子結構變化必會和環境分子的結構變化產生耦合,因此正確的拆分是:總重組能=內重組能+外重組能+耦合項。
然而,文獻里看到的都是這么拆分的:總重組能=內重組能+外重組能。顯然這種劃分方式并不確切,除非在計算的時候,把耦合項給納入到了內重組能或外重組能當中。比如納入到外重組能的話,那么就需要計算總重組能和內重組能,然后求差值來得到外重組能,而不是直接按1.1節的方式來計算外重組能。
很多文章雖然研究的是晶體內的電子/空穴轉移,但是算的卻是分子在孤立狀態的重組能。前面提到的《使用Dushin分解重組能和計算Huang-Rhys因子》也是算的吡咯在孤立狀態的重組能。JACS,130,12377中指出氣相算的分子孤立狀態的重組能可以作為分子晶體環境下內重組能的較好近似。所以,如果研究分子晶體中電荷轉移速率問題時嫌按照上文計算太麻煩,干脆就只計算分子在孤立狀態的重組能,這在步驟上容易多了,耗時也低多了。
2 溶液下外重組能的計算
溶液下算外重組能可以用顯式溶劑模型也可以用隱式溶劑模型。
用顯式溶劑模型的話,計算外重組能的步驟、方法選用等方面和上面說的完全一樣,只不過不太適合用PBC來算,而更適合按照團簇來算。計算時必須考慮各種溶劑層排布方式,這是非常麻煩的事情,為此通常得做動力學模擬來得到一批溶質+溶劑微結構,都分別計算外重組能之后再取平均。
用隱式溶劑模型來算外重組能就很方便也很快捷了,這牽扯到非平衡溶劑效應。溶劑的快部分對應于溶劑的電子結構改變,慢部分對應于溶劑的結構和朝向的改變。只讓溶劑的快部分響應溶質的話,相當于溶劑-溶質之間電子結構已經相互極化到自洽,但溶劑幾何結構還沒弛豫。而快部分和慢部分都響應溶質的話,就相當于溶劑的電子結構和幾何結構都充分弛豫了。這兩種情況的能量差正是外重組能。關于非平衡溶劑效應以及使用方式的介紹,參見《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》(http://www.shanxitv.org/314)。一般靠隱式溶劑模型表現非平衡溶劑都是用于電子垂直躍遷過程的研究,但計算外重組能其實也正好用得著。
隱式溶劑模型下計算外重組能流程如下
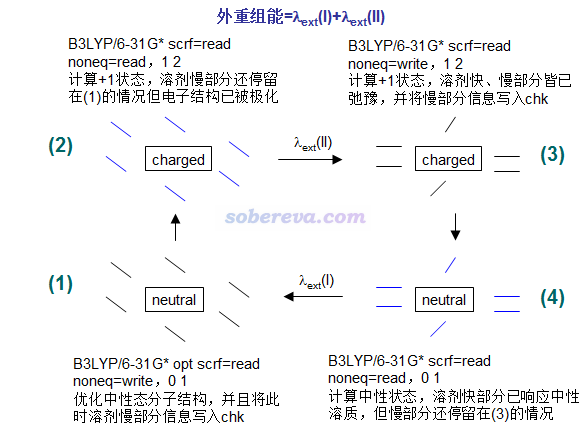
圖中給出了對應的Gaussian09的關鍵詞,noneq=xxx是寫在坐標末尾后空一行處。0 1、1 2是電荷與自旋多重度設定,假定計算的是溶質在中性和帶+1電荷之間變化的外重組能。圖中雖然畫了溶劑分子,但那只是示意,在隱式溶劑模型下溶劑分子是當做沒有具體結構的連續介質考慮的。
按照上面的計算流程,這里舉一個萘分子在水中的外重組能的實例,下面是每一步的能量
(1)-385.8964554
(2)-385.6405968
(3)-385.6810581
(4)-385.8560789
λext(I)=27.2114*(-385.6405968+385.6810581)=1.10eV
λext(II)=27.2114*(-385.8560789+385.8964554)=1.10eV
故外重組能為λext(I)+λext(II)=2.20eV。
在氯仿下計算的結果
(1)-385.895197
(2)-385.6473217
(3)-385.6668006
(4)-385.8762549
λext(I)=0.53eV
λext(II)=0.52eV
故外重組能為1.05eV。趨勢是溶劑的介電常數越小外重組能也就越小。