使用Multiwfn極為方便地繪制(超)極化率密度和三維空間對(超)極化率的貢獻
使用Multiwfn極為方便地繪制(超)極化率密度和三維空間對(超)極化率的貢獻
文/Sobereva@北京科音 2023-Aug-11
1 前言
(超)極化率密度是一種非常重要的直觀分析化學體系(超)極化率內在本質的方法,由此可進一步得到三維空間各個位置對(超)極化率的貢獻,這種分解分析對于討論和對比(超)極化率的大小和符號,以及深入了解體系不同區域對外電場的響應,都有重要意義。筆者之前在《使用Multiwfn計算(超)極化率密度》(http://www.shanxitv.org/305)介紹了如何利用強大靈活的波函數分析程序Multiwfn以純手動的方式計算(超)極化率密度,此方法已經在大量文章中得到了廣泛的應用。但這種做法操作起來很費事,計算流程也容易忘,經驗不足的用戶還可能犯錯誤,在一定程度上制約了(超)極化率密度的普及。
2023-Aug-11更新的Multiwfn版本中加入了非常方便省事的計算(超)極化率密度以及三維空間對(超)極化率的貢獻的功能,可以直接繪制等值面圖和平面圖,令這種分析的流程極大地簡化,也充分避免了初學者在操作過程中犯錯的可能,在本文就介紹一下這個功能的用法。《使用Multiwfn計算(超)極化率密度》(http://www.shanxitv.org/305)里介紹的操作方法就可以徹底棄了,但如果你對(超)極化率密度的背景知識不了解、不知道怎么分析的話,則一定要先讀一下這篇文章里的相關介紹和討論,我假定讀者已經看過了此文。
Multiwfn可以在官網http://www.shanxitv.org/multiwfn免費下載。如果你對Multiwfn不了解,建議閱讀《Multiwfn入門tips》(http://www.shanxitv.org/167)和《Multiwfn FAQ》(http://www.shanxitv.org/452)。本文介紹的功能需要結合Gaussian使用,本文例子用的是Gaussian 16 C.02版,至少不能用比G09 B.01更老的版本。
下文涉及的文件都可以在http://www.shanxitv.org/attach/683/file.zip中找到。
2 實例1:D-pi-A體系第一超極化率密度的繪制
此例要對下面這個D-pi-A型體系繪制第一超極化率密度的XX分量(ρxx),以及三維空間對第一超極化率的貢獻(-x*ρxx)。在Multiwfn可執行文件包里examples\excit\D-pi-A.fchk文件記錄的結構信息對應的是此體系的優化過的基態的結構,如下圖所示。
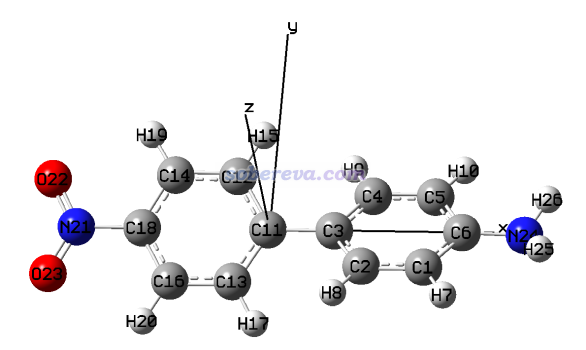
啟動Multiwfn,然后輸入
examples\excit\D-pi-A.fchk //Multiwfn將從中讀取結構信息。用.xyz、.pdb、.gjf等其它記錄了結構信息的文件格式也都可以,詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)
24 //各種(超)極化率相關的分析
3 //(超)極化率密度分析
2 //計算第一超極化率密度
1 //X方向
1 //產生不同電場下的Gaussian單點任務的輸入文件
現在當前目錄下就有了X-1.gjf、X_0.gjf和X+1.gjf。Multiwfn用的電場的有限差分步長是0.003 a.u.,這很適合用于計算(超)極化率密度,也因此比如X-1.gjf和X+1.gjf就分別對應向X的負方向和正方向加0.003 a.u.電場,X_0.gjf是不加外電場的情況。輸入文件里默認用的是PBE0/aug-cc-pVTZ進行計算,這對于大多數分子的(超)極化率的計算都是適合的級別,如果想改成其它的自己改就完了。輸入文件里還有一些關鍵詞是用來盡可能避免因為帶彌散函數較多時電子積分求解精度差和KS矩陣構建不精確而導致SCF難收斂的,不懂就別亂改。nosymm關鍵詞也自動加上了,由此避免Gaussian自動把體系搞到標準朝向下,不理解的話看《談談Gaussian中的對稱性與nosymm關鍵詞的使用》(http://www.shanxitv.org/297)。從gjf文件內容還可以看到這些任務會產生與輸入文件同名的.wfx格式的波函數文件。
使用Gaussian運行這三個.gjf文件,分別得到X-1.wfx、X_0.wfx和X+1.wfx。如果你不知道怎么批量用Gaussian運行一堆gjf文件的話,看《使用Gaussian時的幾個實用腳本和命令》(http://www.shanxitv.org/258)。
接著,在Multiwfn的窗口里輸入2,并輸入這些wfx文件所在目錄(如果是在當前目錄下則直接按回車),它們就都被讀取了。之后看到新菜單,選項的含義都提示得非常明白,可以對(超)極化率密度和三維空間對(超)極化率的貢獻計算格點數據(之后可以繪制等值面圖或者導出cub文件),也可以對它們繪制成平面圖。由于一開始我們選的是第一超極化率和X方向,所以此菜單的選項里的first hyperpolarizability density當前顯然指的是ρxx,而spatial contribution to first hyperpolarizability顯然對應-x*ρxx。
下面繪制ρxx的等值面圖。在Multiwfn里輸入
1 //計算(超)極化率密度的格點數據
3 //高質量格點。不懂格點怎么選的話看《Multiwfn FAQ》(http://www.shanxitv.org/452)的Q39
之后屏幕上給出了積分值(-1.721222 a.u.)。選1后蹦出了ρxx的等值面圖。等值面數值設為2后看到的圖像如下,綠色和藍色分別為正值和負值等值面
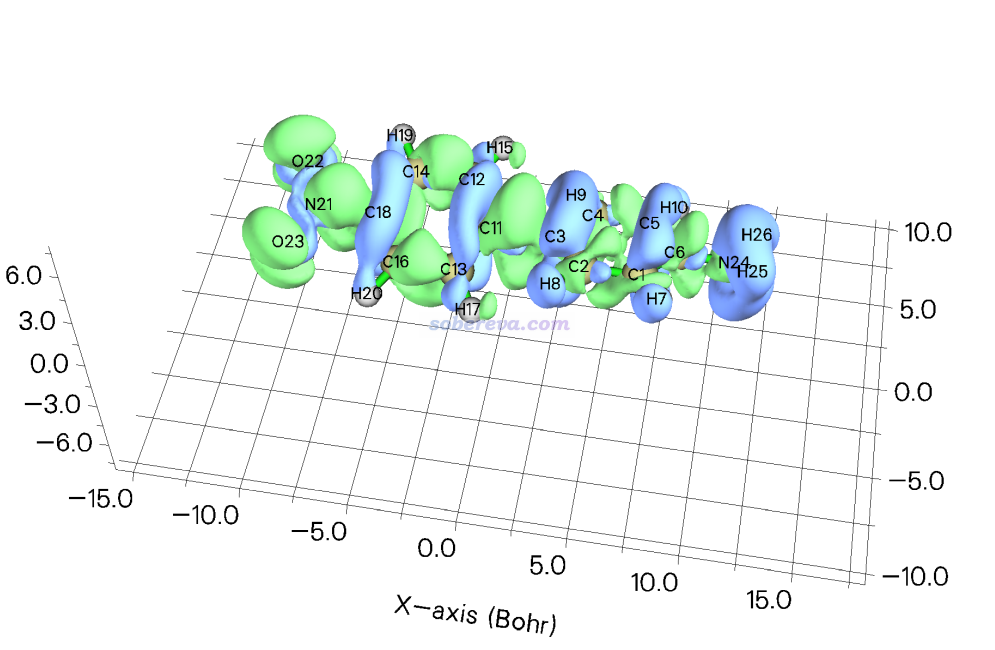
關閉窗口后還可以選2導出cub文件,然后可以用《在VMD里將cube文件瞬間繪制成效果極佳的等值面圖的方法》(http://www.shanxitv.org/483)介紹的方法在VMD里繪制出效果更好的等值面圖。
接下來繪制-x*ρxx的等值面圖,輸入
0 //返回
2 //計算三維空間對(超)極化率密度貢獻的格點數據
3 //高質量格點
屏幕上顯示格點數據的積分值為7803.891517 a.u.,這對應基于立方格點積分-x*ρxx算的βxxx值。選1后蹦出了-x*ρxx的等值面圖。等值面數值設為5時看到的圖如下(這里還改成了solid+mesh風格顯示以讓圖更有立體感)。可見圖里大部分地方數值為正,是此體系βxxx很大的主要原因。
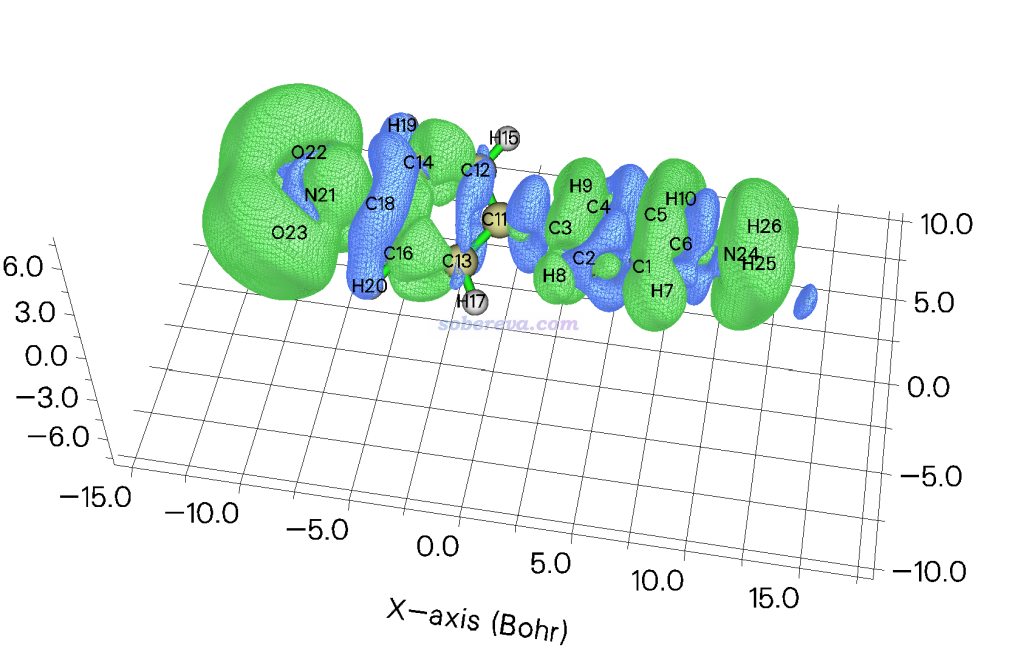
選0返回后還可以選3和4分別繪制ρxx和-x*ρxx的平面圖,操作和設置方式與Multiwfn的主功能4繪制平面圖完全一樣,如果你不熟悉用Multiwfn繪制平面圖的話參看Multiwfn手冊4.4節的海量例子。平面圖的繪制在下一節的例子里有具體體現。
在本文的文件包里的D-pi-A目錄里有個gamma.out,是PBE0/aug-cc-pVTZ級別對當前體系計算(超)極化率的輸出文件。使用《使用Multiwfn分析Gaussian的極化率、超極化率的輸出》(http://www.shanxitv.org/231)介紹的方法查看βxxx會發現數值為7639.07。上面基于立方格點積分得到的值7803.89與之很接近,說明以上圖像是合理、有意義的。
3 實例2:18碳環第二超極化率密度的繪制
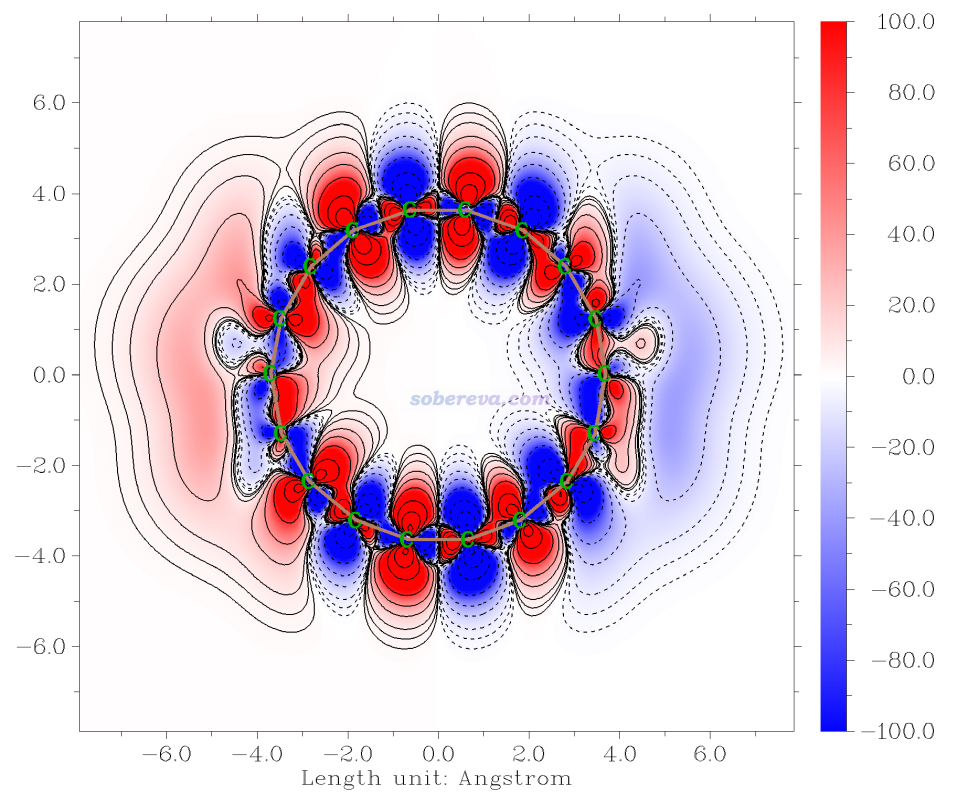
18碳環(cyclo[18]carbon)是個有意思的體系,筆者對它及其類似物做了大量的研究,匯總見http://www.shanxitv.org/carbon_ring.html。在Carbon, 165, 461 (2020)筆者給出了18碳環環平面上的ρxxx和-x*ρxxx的填色等值線圖,這里來重現一下。優化過的18碳環的結構是本文文件包里的C18目錄下的C18.xyz,如下所示,體系在Z=0的XY平面上
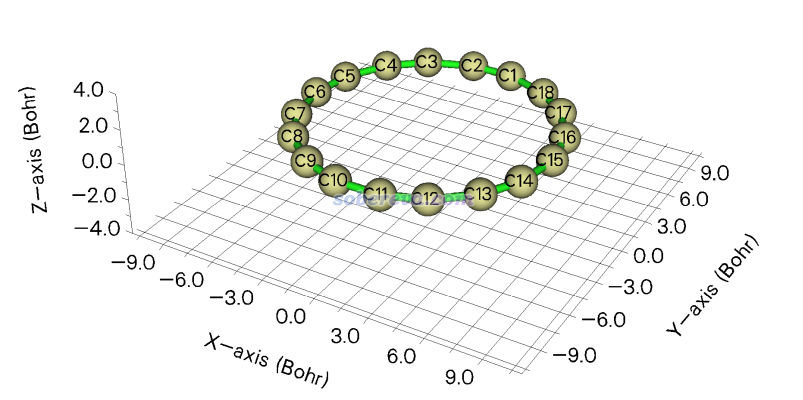
啟動Multiwfn,然后輸入
C18.xyz
24 //(超)極化率分析
3 //考察(超)極化率密度
3 //第二超極化率密度及三維空間對第二超極化率的貢獻
1 //X方向
1 //產生不同電場下的Gaussian單點任務的輸入文件
[回車] //凈電荷為0、自旋多重度為1
當前目錄下產生了X-2.gjf、X-1.gjf、X+1.gjf和X+2.gjf。如我在Carbon, 165, 468 (2020)中證明的,PBE0無法正確描述18碳環的長短鍵交替的結構,因此手動把這4個gjf文件里的PBE0替換成非常適合研究碳環體系的wB97XD。然后用Gaussian計算它們,得到X-2.wfx、X-1.wfx、X+1.wfx和X+2.wfx。
在Multiwfn的窗口里輸入2,并輸入這些wfx文件所在目錄以載入它們。之后繪制ρxxx的平面圖,輸入
3 //繪制(超)極化率密度的平面圖
1 //填色圖
[回車] //用默認格點數
1 //XY平面
0 //Z=0
圖像馬上就蹦出來了。之后關閉圖像,輸入以下命令調節作圖效果
19 //修改色彩變化
8 //藍-白-紅
1 //設置色彩刻度下限和上限
-100,100
4 //顯示原子標簽
12 //深綠色
8 //顯示化學鍵
14 //棕色
-8 //把橫縱軸單位改成埃
-2 //設置X、Y、Z(色彩刻度)軸的標簽間隔
2,2,20
-3 //其它設置
2 //設置X、Y、Z軸標簽的小數點位數
1
1
1
0 //返回
2 //顯示等值線
3 //修改等值線設置
4 //刪除某些等值線(這里把數值很小的刪除,免得圖像太亂)
32-41
4 //刪除某些等值線
1-10
1 //保存并返回
-1 //重新作圖
現在得到下圖,可見效果很好。-x*ρxxx的平面圖也可以以類似方式繪制,選-5返回后,再選擇4 Plot plane map of spatial contribution to second hyperpolarizability然后重復上面的操作即可。顯然,也可以類似上一節的例子選擇相應選項繪制ρxxx和-x*ρxxx的等值面圖。
4 總結
本文演示了Multiwfn專門計算(超)極化率密度以及三維空間對(超)極化率貢獻的功能,通過上面的例子可見用此功能繪制等值面圖和等值線圖非常方便,照著屏幕上的提示來操作就可以輕易完成,此功能使得(超)極化率密度的考察變得比以往容易得多得多,推薦大家在極化率和超極化率的研究中充分使用此功能。本文沒有專門給出極化率密度和三維空間對極化率貢獻的計算例子,因為操作和上面的例子完全一樣,只不過進入主功能24的子功能3之后先選擇1 Polarizability density and spatial contribution to polarizability即可。
Multiwfn還可以基于三維空間對(超)極化率貢獻的格點數據通過模糊空間積分來得到原子對(超)極化率貢獻的定量數值,做法在《使用Multiwfn計算(超)極化率密度》(http://www.shanxitv.org/305)的第7節演示了,這里不再重復。怎么把格點數據導出在上面的例子里已經明確提過了。
使用Multiwfn按本文的做法進行研究時需要在寫文章時引用Multiwfn啟動后明確顯示的Multiwfn原文。