使用concvar程序求解復雜化學反應中物質的濃度隨時間的變化
使用concvar程序求解復雜化學反應中物質的濃度隨時間的變化
文/Sobereva@北京科音 (非正式版)
1 前言
最近有人在計算化學公社論壇問“請問常溫下像是如下述兩條路徑的反應,哪個更優勢”,他給的圖如下所示。
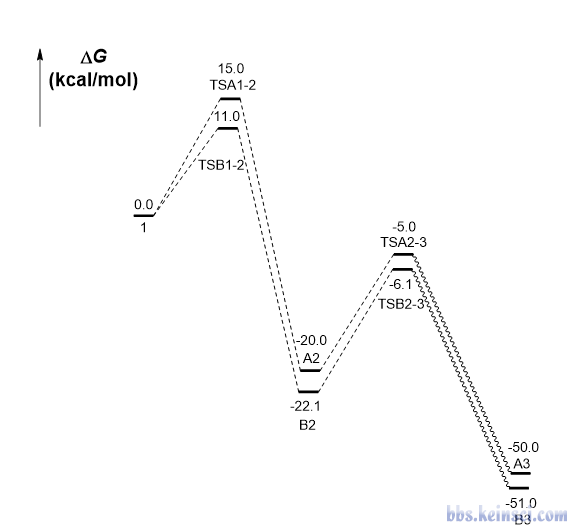
這個問題光憑感覺不容易給出絕對可靠的答案,而這類問題在通過計算化學研究化學反應相關問題時卻又容易遇到。實際上這種問題可以根據每一步的反應速率常數直接模擬反應的進行來得到,這樣的模擬可以給出濃度隨時間的變化。給反應物設置一定初始濃度,并經過足夠長時間的模擬后,哪個是主產物自然就知道了。
目前并沒有免費、靈活、易用的程序實現上述這種模擬,而這樣的程序對于涉及化學動力學的研究問題又非常重要,于是筆者開發了名為concvar的程序彌補這一空白。用戶只需要提供整個反應涉及的各個極小點和過渡態結構的自由能,并設置模擬條件,程序就能開始模擬,輸出各個物質濃度隨時間的變化。
concvar程序的Windows和Linux版可執行文件,以及很詳細的手冊,可以在http://www.shanxitv.org/soft/concvar免費下載。
concvar的介紹文章已經發表在了ChemRxiv上(https://doi.org/10.26434/chemrxiv-2022-r6rh8),研究文章中使用了concvar程序的話必須進行引用(注意確保DOI號在文獻列表里確實顯示了出來),格式例如:Tian Lu, concvar: A program solving time-dependent concentration variation for complex reactions, ChemRxiv (2022) DOI: 10.26434/chemrxiv-2022-r6rh8。
2 concvar簡介
concvar程序的細節、具體使用方法請讀者自行看手冊和發表在ChemRxiv上的原文,在這一節僅對concvar的特征做很簡要的說明。
一個復雜反應包含多個基元反應。concvar主要目的是求解復雜反應中涉及的各個物質(指反應物、中間體、產物,后同)各個時刻的濃度。需要從t=0時刻基于給定的初始濃度在特定溫度下進行模擬,直到達到預設的步數上限,或者滿足預設的某個濃度條件為止。每一步concvar按照下式令各個物質濃度c發生變化,其中t是當前時刻,Δt是模擬步長,t+Δ是下一時刻
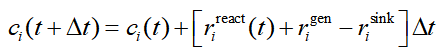
上式中r是反應速率,包含三個來源。其中r_react體現的是相關的基元反應產生的貢獻,如下所示。這里假設基元反應是單分子的情況,concvar也支持雙分子。其中j循環與當前物質i相鄰的其它物質。k(j→i)是相鄰物質j變成i的反應速率常數,k(i→j)是i變成相鄰物質j的反應速率常數。
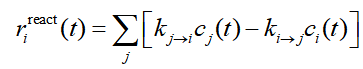
k可以讓concvar根據輸入文件里各個體系(“體系”指極小點和過渡態,后同)的自由能直接根據標準的過渡態理論自動算出來。對于有特殊情況時(如需要考慮隧道效應、變分過渡態理論),k也可以根據《基于過渡態理論計算反應速率常數的Excel表格》(http://www.shanxitv.org/310)或使用其它程序自行計算,然后寫在輸入文件里提供給concvar。
上面物質濃度變化的式子里還有c(gen)和c(sink),這是由于外部原因導致物質濃度生成(generation)和下降(sink)的速率。這兩項在輸入文件里可設可不設,默認為0。concvar也允許令特定物質濃度恒定在特定值。concvar還能強行讓一批物質的濃度在每一步都彼此間滿足Boltzmann分布。
模擬步長的選取是個重要問題。模擬的總時間長度等于步數和步長的乘積,跑特定時間長度的模擬,顯然步長越大,所需步數越少,模擬耗時也因此越少。但步長不能太大,否則會造成結果不精確甚至明顯不合理。假設所有基元反應都是單分子反應,或者雖然有雙分子反應但其中一個反應物濃度為1 M(M是mol/L的意思),則以s(秒)為單位的步長應小于0.1/k_max,其中k_max是模擬涉及的基元反應中最大的k(對單分子以/s為單位,對雙分子以/M/s為單位)。這等同于讓物質濃度每一步的變化不超過當前濃度的10%。concvar在計算一開始會直接列出各個基元反應的k,并給出以此式估計的最大可接受步長,用戶可以以此為參考設置輸入文件里的步長。
3 concvar的應用實例
下面給出concvar程序的一些應用實例,由此讀者可以快速了解concvar都能干什么,有什么實際意義,以及輸入文件的形式是怎樣的。具體輸入文件的寫法請大家自行看手冊里的詳細說明。下文的例子的完整的輸入、輸出文件在程序文件包里的examples目錄下都提供了。concvar非常靈活,請讀者基于這些例子舉一反三研究自己的實際問題。
3.1 基元反應
在使用concvar研究復雜情況之前,先看一個最簡單的情況,基元反應,能量折線圖如下所示,藍字是體系序號(標注順序隨意,這決定了$G字段里定義能量的順序)。由于逆反應能壘很高,因此逆反應可以忽略不計。
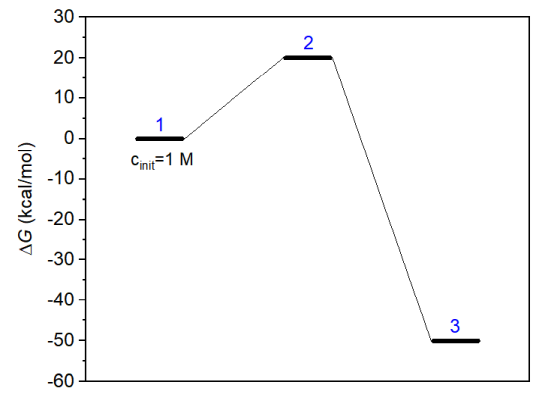
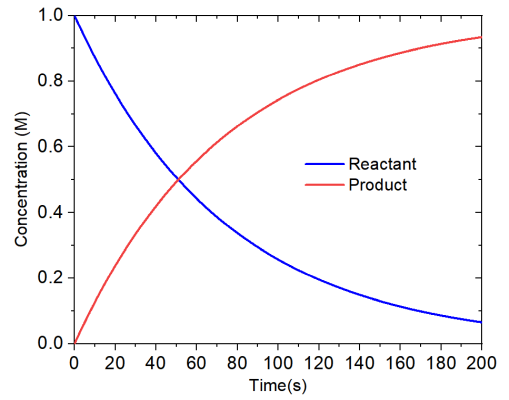
我們要對此反應在298.15 K下模擬200秒,看看反應物和產物濃度是怎么變化的。此例的concvar輸入文件如下所示(創建一個文本文件,把以下內容粘貼進去即可,末尾至少要有一個空行。$打頭的代表字段,不同字段間必須有至少一個空行)。
temper= 298.15
stepsize= 1E-4
nstep= 2000000
outfreq= 1000
ioutfmt= 2
$G
0
20
-50
$link
1,2,3
$cinit
1 1.0
上面temper是模擬溫度(K),stepsize是模擬步長(秒),nstep是模擬步數上限,outfreq是往輸出文件中輸出各物質當前濃度的頻率,ioutfmt控制輸出的濃度的格式(1是科學計數法,2是小數)。$G字段設置各個體系在當前溫度下的標準態濃度的自由能(kcal/mol)。由于能量折線圖上我們把反應物、過渡態、產物分別標記為1、2、3號體系,因此$G里也要按照反應物、過渡態、產物的順序輸入。自由能可以通過量子化學方法很容易地計算,參考《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552)。$link里每一行定義一個基元反應的反應物、過渡態、產物的體系序號。$cinit設置物質的初始濃度,當前將反應物(1號體系)濃度被設為1 M,沒設的默認為0。
啟動concvar,輸入輸入文件的路徑(Windows版可以直接把文件圖標拖到concvar窗口里免得手寫路徑。如果路徑兩邊自動出現了雙引號要去掉),然后按回車,就可以看到如下模擬狀態信息,然后程序開始進行模擬。從以下信息中可看到各個物質的自由能,以及每個基元反應的自由能壘和根據過渡態理論估計的反應速率常數。還可以看到concvar建議步長應當小于7.36秒,當前我們用的步長0.0001秒遠小于這個,所以模擬結果肯定是相當精確的。
Temperature: 298.150 K
Simulation stepsize: 1.000E-04 s
Number of simulation steps: 2000000
Total simulation time: 200.000000 s ( 3.333333 min)
Output frequency: per 1000 steps ( 0.100000 s)
Number of systems: 3
Number of minima: 2
1 # System index: 1, G: 0.00 kcal/mol, c(init): 1.000000 M
2 # System index: 3, G: -50.00 kcal/mol, c(init): 0.000000 M
Number of reactions: 2
1 # System 1 to 3, G barr: 20.00 kcal/mol, k: 1.358867E-02 s^-1
2 # System 3 to 1, G barr: 70.00 kcal/mol, k: 3.040630E-39 s^-1
Maximum k is 1.358867E-02 s^-1
Stepsize is suggested to be smaller than 7.36E+00 s for present situation
在模擬進行過程中,程序每隔outfreq步就會往當前目錄下的conc.txt里輸出當前的步數、時間、各個物質的濃度以及總濃度。模擬期間用戶可以隨時打開此文件,看看當前濃度已經變化成什么樣了。在筆者的Intel i7-10870H普通CPU上僅花費了3秒就跑完了設定的200萬步。最后conc.txt的內容如下所示。
Step Time(s) 1 3 Total
0 0.0000E+00 1.0000000 0.0000000 1.0000000
1000 1.0000E-01 0.9986421 0.0013579 1.0000000
2000 2.0000E-01 0.9972860 0.0027140 1.0000000
3000 3.0000E-01 0.9959317 0.0040683 1.0000000
...略
1997000 1.9970E+02 0.0662937 0.9337063 1.0000000
1998000 1.9980E+02 0.0662037 0.9337963 1.0000000
1999000 1.9990E+02 0.0661138 0.9338862 1.0000000
2000000 2.0000E+02 0.0660240 0.9339760 1.0000000
可見在反應進行200秒之后,反應物(1號體系)的濃度僅有0.066 M,產物濃度為0.934 M,模擬期間總濃度始終為1 M。
可以將濃度變化曲線畫出來直觀考察濃度變化過程。啟動Origin,把conc.txt往里面一拖,然后把第二列作為橫坐標數據,第3、4列作為縱坐標數據,繪制曲線圖,結果如下,可見反應物濃度逐漸下降,產物濃度逐漸上升
下面,我們用concvar考察一下這個反應的半衰期,也就是反應物濃度下降到一半的時候所花費的時間,這可以給輸入文件添加以下內容來實現。這代表當1號體系濃度下降到0.5 M以下時模擬就立刻停止。
$conccrit
1 < 0.5
用新的輸入文件重新進行模擬,模擬會中途結束,并顯示以下信息。即曰,模擬到了51.0092秒的時候就滿足了濃度判斷條件,顯然當前的反應半衰期就是51.0092秒。
Simulation is stopped because concentration of 1 < 0.500000 M has been satis
fied at step 510092 ( 51.00920000 s). Current concentration: 5.0000E-01 M
單分子基元反應的半衰期是有解析解的,即ln(2)/k。從concvar載入輸入文件后顯示的信息中可看到當前的正向反應的k是1.358867E-02 s^-1,因此精確的半衰期是ln(2)/1.358867E-02=51.0092秒,這和concvar模擬出來的精確吻合!體現出當前模擬是完全合理的。實際上,當前模擬用更大步長也完全可以,比如模擬步長從0.0001設大到0.001秒的話,就只需要1/10的模擬耗時,此時得到的半衰期是51.009秒,依然很精確,只不過在有效位數上輕微微打了折扣。
3.2 包含多個基元步的復雜反應
此例使用concvar對下面的能量折線圖描述的情況進行模擬。可見有三個基元反應,1和7號分別是反應物和產物,2、4、6號是過渡態,3和5是中間體。每個基元反應的正向和逆向勢壘都分別是15和20 kcal/mol。
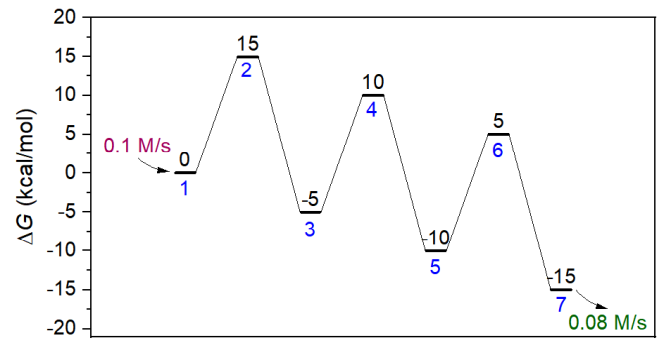
此模擬假定所有物質的初始濃度都為0,反應物的生成速率為0.1 M/s,而產物的消耗速率是0.08 M/s。模擬的反應將在250 K下進行50秒。輸入文件如下所示,$G按照體系序號的順序來寫。順帶一提,$G定義的是相對自由能,相對于誰都可以,只有自由能之差影響模擬結果,習俗上將反應物作為自由能零點來定義。由于有三個基元反應,所以$link里定義了三條連接關系。$gen和$sink分別定義反應物和產物的生成和消耗速率。注意消耗速率具體來說是最大消耗速率,每一步消耗量不會超過剩余量(當某一步某物質濃度為負時,concvar自動會將其濃度設為0)。
temper= 250
stepsize= 1E-4
nstep= 500000
outfreq= 100
ioutfmt= 2
$G
0
15
-5
10
-10
5
-15
$link
1,2,3
3,4,5
5,6,7
$gen
1 0.1
$sink
7 0.08
使用concvar載入上面的輸入文件進行模擬,一開始會顯示以下信息。建議用戶總是仔細看一下這里顯示的模擬參數,確保輸入文件書寫和載入正確。
Number of systems: 7
Number of minima: 4
1 # System index: 1, G: 0.00 kcal/mol, c(init): 0.000000 M
2 # System index: 3, G: -5.00 kcal/mol, c(init): 0.000000 M
3 # System index: 5, G: -10.00 kcal/mol, c(init): 0.000000 M
4 # System index: 7, G: -15.00 kcal/mol, c(init): 0.000000 M
Generation and consumption rates:
1 # System index: 1, gen.: 0.100000 M/s, consump.: 0.000000 M/s
2 # System index: 3, gen.: 0.000000 M/s, consump.: 0.000000 M/s
3 # System index: 5, gen.: 0.000000 M/s, consump.: 0.000000 M/s
4 # System index: 7, gen.: 0.000000 M/s, consump.: 0.080000 M/s
Number of reactions: 6
1 # System 1 to 3, G barr: 15.00 kcal/mol, k: 4.018411E-01 s^-1
2 # System 3 to 1, G barr: 20.00 kcal/mol, k: 1.710605E-05 s^-1
3 # System 3 to 5, G barr: 15.00 kcal/mol, k: 4.018411E-01 s^-1
4 # System 5 to 3, G barr: 20.00 kcal/mol, k: 1.710605E-05 s^-1
5 # System 5 to 7, G barr: 15.00 kcal/mol, k: 4.018411E-01 s^-1
6 # System 7 to 5, G barr: 20.00 kcal/mol, k: 1.710605E-05 s^-1
Maximum k is 4.018411E-01 s^-1
Stepsize is suggested to be smaller than 2.49E-01 s for present situation
輸出的concvar.txt開頭部分如下所示,可見反應物、中間體、產物的濃度隨時間的變化都輸出了。
Step Time(s) 1 3 5 7 Total
0 0.0000E+00 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
100 1.0000E-02 0.0009980 0.0000020 0.0000000 0.0000000 0.0010000
200 2.0000E-02 0.0019920 0.0000080 0.0000000 0.0000000 0.0020000
300 3.0000E-02 0.0029820 0.0000179 0.0000001 0.0000000 0.0030000
...略
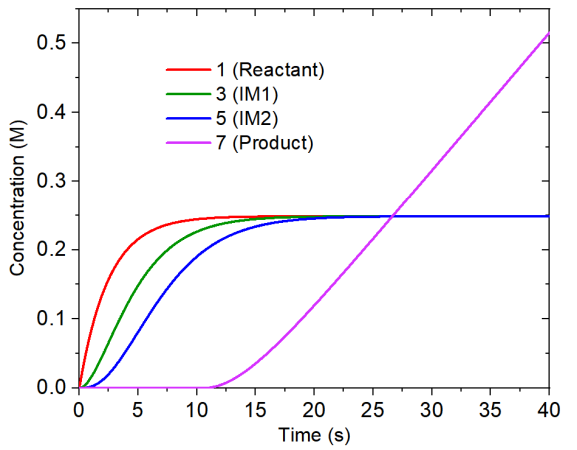
對concvar.txt里的濃度變化進行繪圖,得到下圖。可見隨著反應物的不斷產生,反應物、第一個中間體(體系3)、第二個中間體(體系5)的濃度依次累積起來,但到了20秒后基本就不變了,處于飽和了。產物的濃度在10.7秒之前都為0,這是因為自設的產物的消耗速率0.08 M/s在此之前都比它的產生速度更快。在反應進行20秒之后,產物的濃度以0.02 M/s的速率線性增加,這是因為此時第二個中間體的濃度已經恒定不變了,而且反應物的生成速度(0.1 M/s)比產物的消耗速度(0.08 M/s)更大。
3.3 含有競爭反應的例子
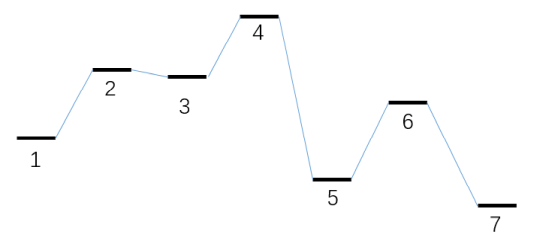
下面這個能量折線圖里各個體系的自由能就是本文一開始的那張圖里的,存在彼此競爭的兩個反應路徑。此例我們靠concvar做模擬來研究一下哪個產物是主產物、反應的選擇性如何。
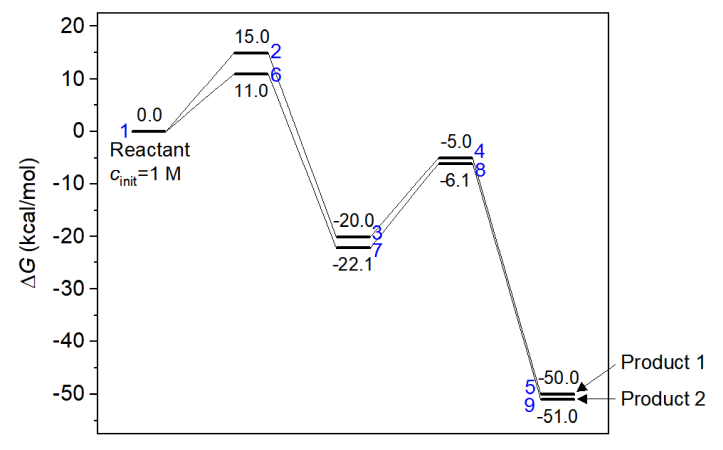
這個反應假定在常溫下進行,反應物初始濃度設1 M。模擬步長用1E-6秒,跑100萬步,因此模擬總時間為1秒。前面說了,concvar會直接在屏幕上顯示最大可接受步長,模擬用的步長明顯比那個小就可以保證模擬精度。至于需要跑多少步,大家可以反復嘗試。如果跑的步數太少,導致模擬的總時間長度不夠,可能產物都還沒怎么生成,就沒法判斷主產物了,此時可以把步數增加后重新跑。此例的輸入文件如下所示。可見在$link里反應物(體系1)同時在兩個基元反應中被涉及。
temper= 298.15
stepsize= 1E-6
nstep= 1000000
outfreq= 1000
ioutfmt= 2
$G
0
15
-20
-5
-50
11
-22.1
-6.1
-51
$link
1,2,3
3,4,5
1,6,7
7,8,9
$cinit
1 1.0
這次的模擬輸出文件如下所示
Step Time(s) 1 3 5 7 9 Total
0 0.0000E+00 1.0000000 0.0000000 0.0000000 0.0000000 0.0000000 1.0000000
1000 1.0000E-03 0.0000000 0.0010982 0.0000699 0.9875062 0.0113257 1.0000000
2000 2.0000E-03 0.0000000 0.0010313 0.0001367 0.9760981 0.0227339 1.0000000
3000 3.0000E-03 0.0000000 0.0009685 0.0001996 0.9648217 0.0340102 1.0000000
...略
997000 9.9700E-01 0.0000000 0.0000000 0.0011681 0.0000093 0.9988226 1.0000000
998000 9.9800E-01 0.0000000 0.0000000 0.0011681 0.0000092 0.9988227 1.0000000
999000 9.9900E-01 0.0000000 0.0000000 0.0011681 0.0000091 0.9988228 1.0000000
1000000 1.0000E+00 0.0000000 0.0000000 0.0011681 0.0000090 0.9988229 1.0000000
5號和9號分別是產物1和產物2。從以上信息可見,在模擬結束后,1 M反應物幾乎完全變成了產物2(0.9988 M),而產物1的濃度幾乎可以忽略不計(約0.0012 M)。當前反應已經進行得很充分了,因為反應物(體系1)、中間體(體系3和7)的濃度都基本為0。因此,此模擬證明產物2是主產物,而且反應的選擇性非常強。
3.4 驗證Curtin–Hammett原理
化學動力學領域有個知名的Curtin–Hammett原理。它說如果有一對反應物彼此可以快速相互轉換,每個反應物都各通向一個產物而且逆反應可以忽略,則產物分布由兩個反應的過渡態的能量相對高低所決定,過渡態能量低的那個路徑對應的是主產物。Curtin–Hammett原理可以通過推導來證明,而這一節我們設計一個模型,用concvar做模擬來驗證。下面的能量折線圖對應的情況是Curtin–Hammett原理適用的典型情況,體系3和5是兩個反應物,它們之間的變換勢壘非常低,因此常溫下二者轉換很快且總能達到熱力學平衡狀態。兩個反應物通向產物的勢壘都較高,并且產物能量顯著低于反應物,故逆反應可忽略。按照Curtin–Hammett原理的說法,由于TS 1顯著低于TS 2,產物1應當是主產物(盡管根據波爾茲曼分布,反應物2的濃度總比反應物1要高,且盡管產物2相對于產物1是明顯熱力學上更有利的產物)。
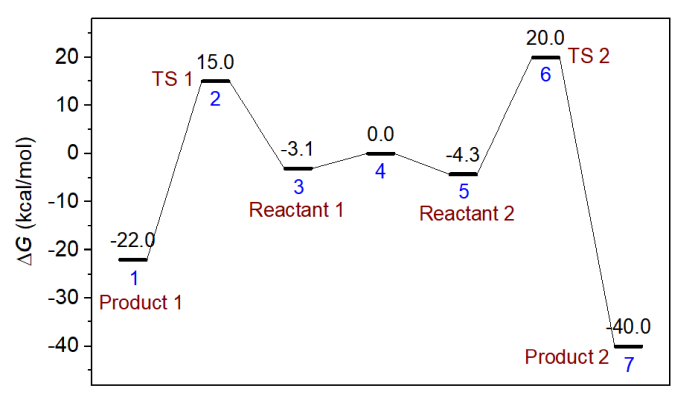
本節我們在298.15 K下對上圖的模型進行模擬來試圖驗證Curtin–Hammett原理對主產物的預測。輸入文件如下所示。這里有很關鍵的一點是不能將兩個反應物之間的相互轉換反應以常規方式進行考慮,即不能在$link里寫上3,4,5,否則由于這樣的基元反應的k很大,必須用非常小的模擬步長(1E-12秒的數量級)才行,而此時為了模擬足夠長時間以觀測到產物出現足夠的濃度(需幾百秒,因為此例的反應勢壘較高),所需要的模擬步數要達到1E14數量級,明顯不可能算得動。考慮到兩個反應物之間的轉換極快,二者總能達到熱力學平衡,因此在此例輸入文件里用了$Boltzmann字段,直接要求它倆的濃度關系在模擬的每一步總是滿足Boltzmann分布(或者說,每一步都將二者的總濃度按照Boltzmann分布關系進行分配)。如果不了解Boltzmann分布的話看《根據Boltzmann分布計算分子不同構象所占比例》(http://www.shanxitv.org/165)。此時,這兩個反應物各自的濃度隨便設,只有濃度之和是有意義的,這里將二者濃度都設為了0.5 M,即總反應物濃度是1 M。
temper= 298.15
stepsize= 1E-3
nstep= 500000
outfreq= 100
ioutfmt= 2
$G
-22
15
-3.1
0
-4.3
20
-40
$link
1,2,3
5,6,7
$Boltzmann
3,5
$cinit
3 0.5
5 0.5
用以上輸入文件進行模擬,反應總共進行了500秒,實際發現到了200秒之后濃度就不再明顯變化了,因此下圖只把前200秒的濃度變化曲線繪制了出來。
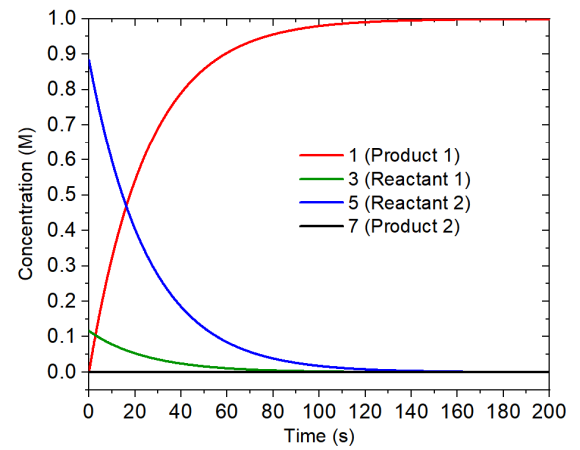
由上圖可見兩個反應物的濃度隨反應進行不斷下降,由于定義了$Boltzmann,二者的比率始終為0.131:1。產物2的濃度始終基本為0,而產物1的濃度則增加得很快,因此是占絕對主導的產物,這和Curtin–Hammett原理做出的預測完全相同。
3.5 確定決速態
這里說的決速態是指它的自由能對整個反應速率起決定作用的過渡態,它的自由能輕微降低就可以令反應速率有明顯的提升。目前有直接觀看能量折線圖判斷決速態的方法,見J. Chem. Educ., 58, 32 (1981)和ChemPhysChem, 12, 1413 (2011),而本節我們通過concvar從數值模擬的角度來確認決速態,這是嚴格而且普適的。
本節考察下圖的模型,1號體系是反應物,經過兩個過渡態到達產物(體系5)。這兩步正向反應勢壘都是30 kcal/mol,哪個是決速態?為了研究這個問題,創建如下輸入文件,假設模擬發生在350 K,反應物初始濃度為1 M。由于這兩個基元反應都很慢,為了讓產物能有明顯的濃度,需要跑較長的模擬。concvar運行后會顯示步長建議不超過55.9 s,因此這里用10秒作為步長(留有一定余量,因為之后還要稍微降低過渡態勢壘后重新模擬,屆時最大可接受步長會更小)。總共模擬10000000步,相當于反應進行100000000秒(3.17年)。
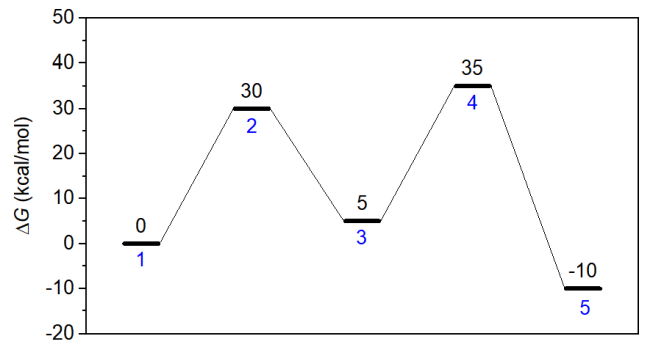
模擬后得到的concvar.txt內容如下所示,可見最終產物(體系5)濃度為0.096783 M。
Step Time(s) 1 3 5 Total
0.0000E+00 0.0000E+00 1.0000E+00 0.0000E+00 0.0000E+00 1.0000E+00
1.0000E+04 1.0000E+05 9.9915E-01 7.5375E-04 1.0122E-04 1.0000E+00
...ignored
1.0000E+07 1.0000E+08 9.0254E-01 6.8087E-04 9.6783E-02 1.0000E+00
將第一個過渡態的濃度降低1 kcal/mol,即把$G里的30改寫為29,然后重新做模擬,發現模擬后產物濃度為0.096836 M,相對于之前基本沒變,體現出總反應速度對這個過渡態的能量敏感性極低。
將過渡態1的自由能恢復為原先值,而把第二個過渡態的自由能降低1 kcal/mol成為34 kcal/mol,再次重做模擬,發現最后產物濃度為0.34796 M,這比原先濃度大得多。可見,第二個過渡態明顯可判斷為決速態。這個結論和前面提到的觀看能量折線圖進行判斷的方法得到的結論是一致的。
3.6 含有雙分子基元反應的復雜反應
前面例子里的模擬只涉及到單分子基元反應,concvar也可以支持含有雙分子反應物和雙分子產物的基元反應情況的模擬,這一節就給出具體例子。需要注意的是,concvar根據輸入的自由能自動計算k的公式適合單分子基元反應以及液相下的雙分子基元反應,如果你的模擬涉及到雙分子氣相基元反應,則相應的k必須自己在$link中直接定義,見concvar手冊3.3節。雙分子氣相基元反應的k可以通過《基于過渡態理論計算反應速率常數的Excel表格》(http://www.shanxitv.org/310)里的表格直接基于自由能壘得到。
本節模擬對應的能量折線圖如下所示。第一個基元反應是雙分子反應物,而第二個基元反應是雙分子產物。下圖的體系2被視為加入分子看待,體系7被視為離去分子看待,在concvar中它們和其它極小點等同視之。記住只有自由能壘影響模擬結果,比如對于第一步基元過程的正向反應,只有G(3)-G(1)-G(2)影響結果,因此只有倆反應物的自由能之和有意義。習俗上,把加入和離去分子的自由能定義為0。
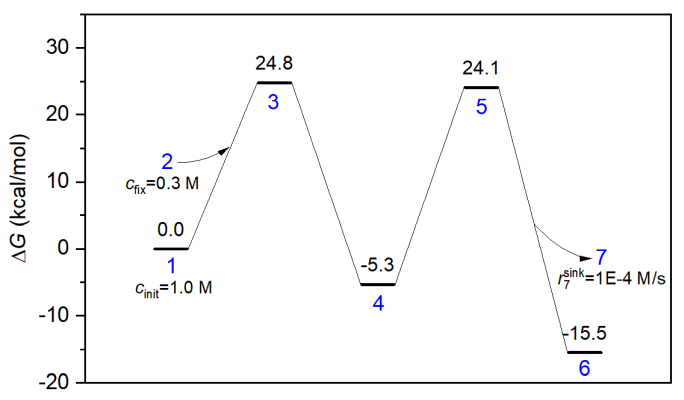
本次模擬用的輸入文件如下。反應在400 K下進行10000秒,反應物的初始濃度被設為了1 M。此模擬假定加入分子的濃度始終恒定為0.3 M,如下所示這通過$fix字段來實現。另外,離去分子的消耗速率假定最大為0.0001 M/s,因此用了$sink字段。怎么定義雙分子反應物和雙分子產物在下面的輸入文件也明確體現了,要用&符號分隔兩個反應物和兩個產物的體系序號。
temper= 400
stepsize= 1E-2
nstep= 1000000
outfreq= 1000
ioutfmt= 2
$G
0
0
24.8
-5.3
24.1
-15.5
0
$link
1&2,3,4
4,5,6&7
$cinit
1 1.0
$fix
2 0.3
$sink
7 1E-4
整個模擬過程中各物質濃度變化如下圖所示。由于反應物和中間體濃度在一開始變化極快,所以橫坐標用了個間斷使得整個過程的各個物質濃度變化都能清楚展現出來。
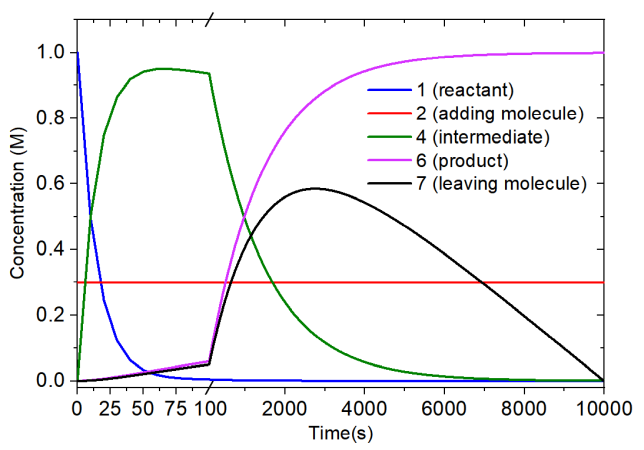
由上圖可見,在模擬開始后幾十秒內,反應物幾乎完全變成了中間體,而加入分子的濃度始終恒定在0.3 M。隨著反應的進一步進行,中間體的濃度逐漸下降并形成了產物。在10000秒反應結束后,1 M的反應物完全變成了產物。離去分子濃度在約2800秒的時候達到了頂峰。而由于此后中間體的濃度較低了,導致由中間體生成產物&離去分子的速度比人為設置的離去分子消耗速度更慢,因此離去分子的濃度不斷下降,并在模擬的最后都消耗光了。
4 總結&其它
concvar是一個免費、靈活、普適的研究復雜反應中各種物質濃度隨時間變化的程序,對于量子化學研究者來說極為友好,只需要把算出來的自由能輸進去并設置模擬條件即可進行模擬。concvar有很大的實際意義,如前面的例子所見,反應的半衰期、反應的主產物和分支比、決速態等都可以通過concvar做模擬來研究。而且仔細考察濃度在反應過程中的變化細節、檢驗濃度變化如何受模擬設置的影響,還可以更好地認識反應的內在特征,認清影響反應進行的因素。大家做量子化學計算研究化學反應的時候可以把concvar模擬的濃度變化納入到文章的討論中,可使得研究更有深度、分析討論更充實。另外,concvar對于物理化學中的化學動力學這部分的教學也很有好處,通過讓學生實際做模擬,可以使他們更好地理解過渡態理論、物質間的變化、反應速率常數、決速態、半衰期、競爭反應等重要概念以及Curtin–Hammett等原理。
最后順帶一提的是,有些復雜反應路徑上有一些勢壘很低、反應很快的基元過程,為了照顧它們需要用很小的步長,導致難以在有限的模擬時間內觀察到真正關心的物質出現明顯的濃度。對這種情況可以考慮對整條反應路徑做適當簡化,將一些濃度沒什么考察意義的中間體和相鄰的過渡態忽略掉。
concvar也可以用于模擬催化循環過程中物質濃度的變化。通常將催化劑與被催化物質的結合作為第一步基元反應,讓催化完成并釋放催化劑對應最后一步基元反應,令最后一步對應催化劑的物質的序號等于第一步的催化劑序號,就構成了首尾相接的催化循環了。