由Mulliken布居和Lowdin布居再談旋轉不變性問題

前言：

最近看到兩篇Mayer的討論Lowdin布居旋轉不變性問題的文章Int. J. Quant. Chem, 106, 2065-2072和CPL, 393, 209-212，受到啟發，繼之前寫的《談談原子軌道朝向引起的量化計算結果與經驗觀念的差異》（http://www.shanxitv.org/52），本文對旋轉坐標問題作進一步討論。

注：本文說軌道時是指原子軌道，極小基與之對應。說原子內基函數時，則含義更為普遍，包括用了擴展基的情況，此時與原子軌道無對應關系。

1. 基本概念回顧

基函數的變換可以分為線性和非線性，常見的都是線性變換，此時變換關系可以用變換矩陣X來表示。設有a基函數集a(1),a(2)...和b基函數集b(1),b(2)...變換矩陣為X；共軛矩陣為X`。則有b(i)=∑[k]X(k,i)a(k)。若有一個算符Y，a為基時叫O，即O(i,j)=<a(i)|Y|a(j)>；b為基時叫P，即P(i,j)=<b(i)|Y|b(j)>。則有P=X`OX。若有一個波函數在a為基時以向量c表示，在b為基時以c"表示，則有c=Xc"。

基函數的酉變換是線性變換的特例，只有當變換前后都是正交歸一集時線性變換才是酉變換，此時X是酉矩陣，即XX`=I。由∑[k]|a(k)><a(k)|=1和∑[k]|b(k)><b(k)|=1的關系可推得矩陣元X(i,j)=<a(i)|b(j)>。

基函數的線性變換在量子化學計算中經常用到，例如由原來不同類型軌道變換為雜化軌道（如s、p軌道組合成sp3軌道），由擴展基變換為自然原子軌道或AOIM軌道，由非正交基函數變換為正交基，由原子基函數變換為群軌道成為分子所屬點群不可約表示的基等等。本文涉及的是由分子旋轉（即朝向改變）導致的基函數變換，這里只討論笛卡爾型高斯函數為基函數的情況，如果是STO、球諧高斯函數，則實際上分子旋轉引起的是其角度部分波函數原點的變化。

有的量化方法有基函數線性變換不變性，例如《談談原子軌道朝向引起的量化計算結果與經驗觀念的差異》已經證明了HF方法的這個特點，在推導中只利用了線性變換的規則。而有的量化方法不具備基函數線性變換不變性，只具備酉變換不變性，Lowdin布居就是如此。

一些引起基函數線性變換的操作在某些條件下可回歸為酉變換，尤其是分子的旋轉操作這點很重要。了解了這些條件，才能正確地使用量化方法。下面先談談重要的原子基函數正交性問題。

2. 原子基函數的正交性

類氫原子軌道：原子內軌道都正交。

STO(Slater type orbitals)：相對于類氫原子軌道修改了徑向部分的形式，使其波節消失，每個STO仍對應于一個原子軌道（雖然高精度計算時也可以用多個STO展開一個原子軌道）。不同類型（指s、p、d...后同）之間的軌道都正交；相同類型不同主量子數軌道間不都正交，不正交情況例如3px與4px。

球諧型GTF(Gaussian type function)：將STO的徑向形式修改為了r^n*exp(-α*r^2)，與原子軌道主量子數不再相關，緊縮或彌散只取決于α值，使用擴展基時與原子軌道無一一對應關系，一般用殼層來描述，一個殼層是指結合一個特定的軌道指數的類型相同的幾個基函數，在此不考慮SP殼層這樣的類型混合的特例。相同殼層內的基函數都正交。不同類型的不同殼層間的基函數都正交，相同類型的不同殼層見基函數不都正交，不正交情況例如分裂價基的兩套殼層間的角度部分行為相同的軌道。

笛卡爾型GTF：將球諧型GTF的角度部分改為x^i*y^j*z^k形式。與球諧型GTF正交性的區別是對于d、f、g...類型的相同殼層內的基函數不都正交，例如d型的XX、YY、ZZ間不正交、f型的XXY與YZZ不正交等等。這是因為對這些情況，將重疊積分中兩個笛卡爾型GTF相乘化為一個GTF后，其i、j、k項都是偶數，所以x、y、z方向積分分量都不為0，故相乘也不為0。球諧型GTF可由笛卡爾型GTF組合得到，詳見《談談5d，6d型d殼層波函數與它們在高斯中的標識》（http://www.shanxitv.org/51）和Int.J.Quant.Chem,54,83-87。

在分子中，以上這些原子基函數由于原子間的重疊，導致原子間的基函數不正交。但注意對于一些半經驗方法，如AM1、PM3，用了重疊矩陣元S(i,j)=δ(i,j)的近似。

3. 旋轉分子引起的基函數的變換

上一篇文章已提到，令坐標軸不動而旋轉分子，等于令分子不動而旋轉坐標軸，由于GTF與坐標軸是綁定的，所以等于對基函數進行了線性變換。變換過程并不會令原子間的基函數發生混合，也不會令不同殼層間的基函數發生混合。如果將基函數按順序排列，則變換矩陣是對角塊形。例如6-31G*（笛卡爾型GTF）的H2O分子因旋轉引起的基函數線性變換矩陣X：


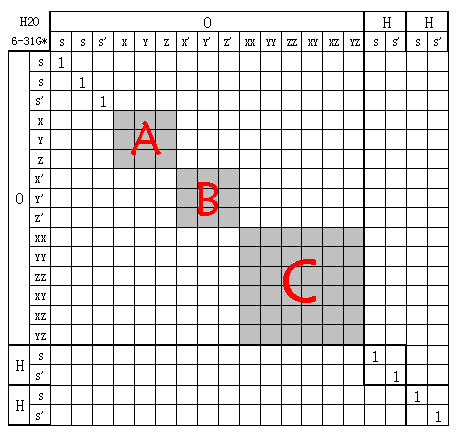
圖中'符號用于區分分裂價基的兩個殼層。灰色區域是未知的不一定是0的值，是多少以及是不是0取決于怎么旋轉。圖中基函數的排序是為了緊湊，描述方便，當然實際量化程序中的基函數排序并不一定是這樣，但并不會對下面的討論結果有什么影響。

現在討論這個矩陣什么時候是酉矩陣。由于旋轉不會改變基函數之間的正交性，如果之前全部原子基函數都正交，旋轉后顯然也都正交，毫無疑問這必然是酉矩陣。但這個條件很難滿足，實際上，旋轉操作的變換矩陣是酉矩陣的條件沒有這么強硬。從圖中可見，由于旋轉只引起殼層內軌道的混合，而殼層間的矩陣元為0，所以只要每個殼層內基函數都正交，則整個變換矩陣就是酉矩陣。同原子的殼層間基函數不完全正交，以及不同原子間基函數不正交這都沒有關系，在旋轉操作中不會“暴露”出來。

可以容易地做出證明。設圖中三個灰色子矩陣分別叫A、B、C，分別對應于三個殼層內基函數的變換。假設使用的基組滿足殼層內軌道正交時，則A、B、C矩陣都是酉矩陣。根據分塊矩陣相乘規則，XX`的三個對角塊就分別是AA`、BB`、CC`，顯然都為單位矩陣，故XX`也為單位矩陣，即X為酉矩陣。

前面提到了，球諧GTF在殼層內基函數正交，所以用這樣基函數時X為酉矩陣，用STO、類氫原子軌道時也是。而用笛卡爾型GTF，如果涉及到d及以上角動量殼層時由于殼層內基函數不完全正交，則旋轉引起的只能說是線性變換。例如上圖中用的是6d軌道，殼層內不都正交，故CC`!=I，所以此時XX`!=I，若在Gaussian中加上5d關鍵詞，即使用球諧型d軌道，則圖中的變換矩陣就是酉矩陣了。

4. Mulliken布居、Lowdin布居與的旋轉不變性問題

Mulliken布居可以寫成矩陣形式，P為密度矩陣，S為重疊矩陣，則PS矩陣的第(i,i)矩陣元就是第i個基函數的Gross原子布居數，也就是這個基函數被Mulliken布居分配到的電子數，顯然∑[k∈α](PS)(k,k)就是α原子的Mulliken電荷。Lowdin布居就是做Mulliken布居之前先用Lowdin正交化方法使全部基函數之間正交化，變換矩陣為X=S^(-0.5)。設P'、C'、S'為正交化后基函數的密度矩陣、系數矩陣（只含占據軌道的展開系數，矩陣元i,j為第j個分子軌道第i個基函數系數）和重疊矩陣，則P'S'=P'=C'C'^(T)=X^(-1)CC^(T)X^(-1)^T=S^(0.5)CC^(T)S^(0.5)^T=S^(0.5)PS^(0.5)，所以S^(0.5)PS^(0.5)的第(i,i)個矩陣元就是Lowdin布居給基函數i分配的電荷。注意由于AM1、PM3等半經驗方法對重疊矩陣近似為單位矩陣，此時Lowdin布居與Mulliken布居是等價的。

電荷布局方法應當具備旋轉不變性，否則分子一旋轉，原子電荷就變了，尤其還會出現等價原子電荷不相等的情況，這是完全沒有物理意義的。Mulliken布居得到的原子電荷具備旋轉旋轉不變性，只需證明旋轉后的∑[k∈α](P'S')(k,k)與旋轉前的∑[k∈α](PS)(k,k)相等即可。

后面的證明需要用到如下關系：
S'=X`SX。當X為酉矩陣時，S'^(0.5)=X`S^(0.5)X，證明見CPL,393,p209-212。
P'=X^(-1)PX`^(-1)。當X為酉矩陣時，可進一步寫為X`PX。

Mulliken布居所得α原子電荷Q(α)=∑[k∈α](PS)(k,k)=∑[k∈α](X^(-1)PX`^(-1)X`SX)(k,k)=∑[k∈α](X^(-1)PSX)(k,k)。
接下來要利用X矩陣為原子對角塊矩陣的性質進行變換。上式繼續寫為∑[k∈α]∑[m]X^(-1)(k,m)(PSX)(m,k)=∑[k∈α]∑[m]∑[n]X^(-1)(k,m)(PS)(m,n)X(n,k)。由于只有m∈α且n∈α時式中X^(-1)(k,m)、X(n,k)才不為0，所以改寫為∑[k∈α]∑[m∈α]∑[n∈α]X(n,k)X^(-1)(k,m)(PS)(m,n)，這就是求X、X^(-1)、PS三個矩陣的原子α的對角塊相乘的矩陣的跡，由于X和X^(-1)的原子α的對角塊相乘為單位矩陣而被消掉，所以最終得到∑[n∈α](PS)(n,n)，可見與旋轉前的∑[k∈α](PS)(k,k)是等價的。這就證明了Mulliken布居得到的原子電荷具備旋轉不變性。

上面的證明只用了X矩陣為原子對角塊的特點，而X不僅有這個特點，由于殼層間不會混合，故更進一步有殼層對角塊的特點，所以可以完全相同地證明Mulliken布居分配給每個殼層的電荷不隨旋轉而改變。但每個殼層內，比如P殼層的X、Y、Z軌道之間經旋轉是混合的，所以分給它們的電荷會經旋轉而改變。但如果是繞比如Z軸旋轉，則Z軌道不參與混合，X矩陣中3*3的P殼層的塊就又分成了2*2的XY的塊和1*1的Z的塊，通過同樣方法又可證明，旋轉后P殼層內只有X、Y軌道上的電子數改變，但二者的總和不變；Z的電子數不變。

再來考察Lowdin布居，先假設X為酉矩陣的情況，看看是否經旋轉后原子電荷也不變，即能否令∑[k∈α](S'^(0.5)P'S'^(0.5))(k,k)回歸到∑[k∈α](S^(0.5)PS^(0.5))(k,k)。
Q(α)=∑[k∈α](S'^(0.5)P'S'^(0.5))(k,k)=∑[k∈α](X`S^(0.5)XX`PXX`S^(0.5)X)(k,k)=∑[k∈α](X`S^(0.5)PS^(0.5)X)(k,k)，然后如同證明Mulliken布居的過程一樣，利用X可視為原子對角塊矩陣特點，可寫為∑[k∈α](S^(0.5)PS^(0.5))(k,k)。所以，旋轉不會令Lowdin布居所得原子電荷改變。

當X不為酉矩陣時，由于S'^(0.5)!=X`S^(0.5)X，上面的推導第一步就不過去。所以只有使用球諧型GTF、STO來滿足旋轉操作的變換矩陣為酉變換條件時Lowdin布居才有旋轉不變性，而用了6d、10f這樣笛卡爾型GTF基函數時則原子電荷會受分子朝向影響。由于X不僅是原子對角塊更是殼層對角塊矩陣，故Lowdin布居是否具有殼層上電子數的旋轉不變性也依賴這個條件。

以上的結論是容易在Gaussian中自行驗證的。Mulliken布居是默認輸出的，用iop(6/80=1)可以輸出Lowdin布居。使用含d基函數的基組，隨便計算一個分子（朝向不要擺正），對比加nosymm與不加nosymm（會令朝向不同）搭配5d和6d（若含f則也考慮7f與10f）的情況，就可以驗證上述結論。但可能由于數值精度和舍入誤差問題使結果末位有一點點差異，不應把這種情況作為不符合旋轉不變性的例子。Lowdin布居盡管在5d下不符合旋轉不變性，但旋轉并不會令電荷變化太大，一般僅在0.01數量級以下，也可能正是因為改變的微不足道而使大家長期忽視了這個問題。而隨著原子的6d、10f型軌道更多的加入基組，這個問題會變得相對更明顯一些。實際上Lowdin布居提出的年代用的還多是STO基組，并沒有這個問題，只是后來大家將之沿用到笛卡爾型GTF基組上，卻忘了考慮這個問題。

5. 基函數變換操作對Mulliken布居和Lowdin布居的一般性影響

可以將X對Mulliken布居和Lowdin布居的影響一般化考慮：X是什么樣對角塊矩陣決定了哪些基函數會混合，變換操作一定會使塊內每個基函數的電子數發生變化；保持塊內基函數電子數之和不改變，對Lowdin布居X必須是酉矩陣，而對Mulliken布居X沒這個要求。X的形狀影響X成為酉矩陣所用基函數條件，僅當每個塊內基函數都正交時X才為酉矩陣。

由此可以將問題拓展考慮。假設旋轉會使同原子內的殼層混合，即令X不具備殼層對角塊特征，則想讓X為酉矩陣從而不令旋轉改變Lowdin布居的原子電荷，則不得不使用在原子內完全正交的基函數；而Mulliken布居則可以隨意選用原子基函數種類。還可以進一步考慮其它基函數變換操作而不限于分子的旋轉。例如要將極小基的CO2分子中每個原子的2px和2py和2s軌道組成不正交的雜化軌道（這里不以常見的sp2方式雜化，因為三個sp2軌道間正交），則變換矩陣X對角線上除了1以外有三個3*3的塊，所以這三個軌道雜化前后電子數一定會變。盡管每個原子的2px、2py、2s之間正交，但變換后的三個雜化軌道間不正交，所以小塊不是酉矩陣，故而X不是酉矩陣，所以用Lowdin布居時三個雜化軌道的布居數之和不等于2px、2py和2s軌道的和。而Mulliken布居的不變性對X是不是酉矩陣沒要求，所以那三個軌道雜化前后布居數總和不變。

旋轉不變性是個容易忽視但又重要的問題，在開發新的量化方法時，應當檢驗方法是否具備這個性質。在實際應用中如果發現某些方法存在這個問題，則不妨撰文討論，以引起更多人的重視。