談談原子軌道朝向引起的量化計算結果與經驗觀念的差異

我曾在《談談5d-6d型d軌道波函數與它們在高斯中的標識》一文中討論到量化程序中的基函數與實際中的原子軌道的對應問題，即6d型笛卡爾GTF函數是難以對應實際實際原子軌道的，這是基函數本身形式的問題。導致對應問題的另一個因素，就是分子的取向問題，它造成了分子軌道組成與常規化學觀念相沖突，比如π鍵。這個問題常常被忽視，很有必要在此討論一下。當然，還有其它因素導致對應問題，比如使用擴展基等等，都給直觀地討論分子軌道的組成帶來了很大困難。（有人提出AOIM、NPA方法來解決基函數與實際原子軌道對應性的問題）

注：下文所說的p軌道，雖然在量化計算中描述它用的函數形式與真實原子軌道波函數是不同的，本質意義也不一樣，但在極小基下，可以近似地將二者畫上等號。下文就假設兩種情況下的差別僅在于本文討論的朝向問題。下文假設量化計算時的坐標系用的是笛卡爾坐標，這樣坐標軸確定，討論起來方便。


首先考慮這樣一個問題。乙烯有π鍵，一般看成是兩個碳原子的類型相同的p軌道組成，比如都是px，它們是垂直于分子平面而平行于某坐標軸的。我們用高斯用極小基計算乙烯，得到圖1中上方的情況。這沒什么問題，從組合系數中可以看到的確由且僅由兩個2px軌道組成。

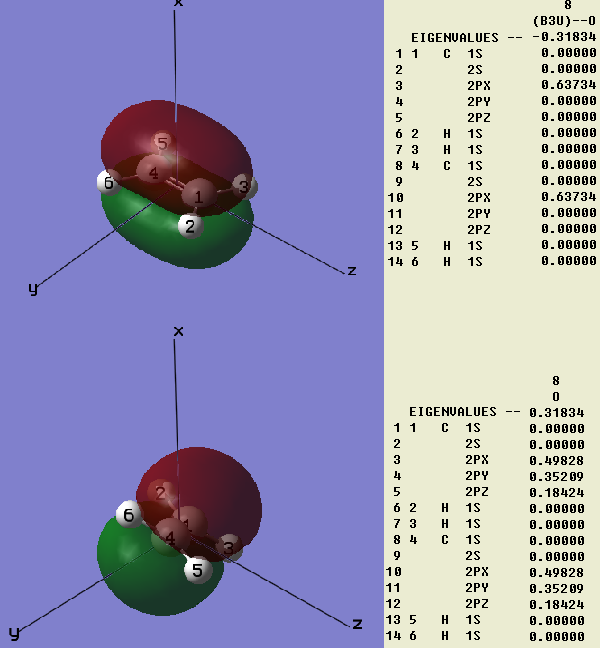
如果將乙烯旋轉一下，并且使用nosymm關鍵字不讓高斯自動重新設置分子的朝向，結果會怎樣？程序中的描述這個p軌道的基函數朝向也會隨之改變么？如果不隨之改變的話，則px軌道將不再垂直于分子平面，π鍵還能形成否？

如果原子軌道朝向會隨分子旋轉而改變，則px/py/pz將不再平行于對應的坐標軸，則其函數形式也必須做變換，這是件麻煩事。更重要的是，若量化程序中的原子軌道朝向不是固定的話，也就是說px/py/pz并非必須平行于對應坐標軸，那么程序如何確定軌道的朝向？對于一個復雜的分子，程序怎么知道每個原子上的原子軌道應該朝向哪個方向？難道也得通過變分方法，改變原子軌道的朝向，使之達到能量最低么？例如圖2的苯，究竟每個碳上的pz軌道的朝向是c、d還是e情況，或者其它情況？顯然，如果程序中各種軌道朝向不是固定的話，會帶來上述很多問題。

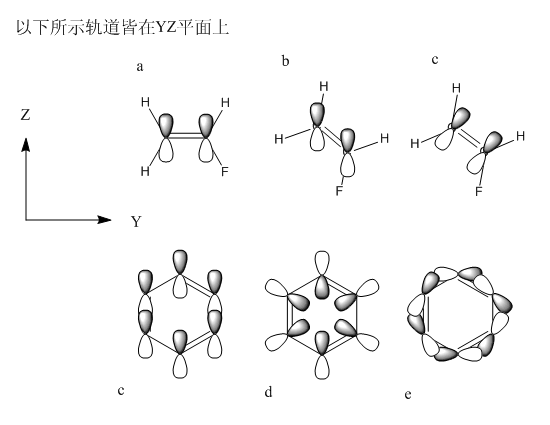
實際上，量化程序中，原子軌道基函數的形式是不隨輸入文件中分子的取向而改變的，也就是說由于坐標軸是固定的，px/py/pz也一定平行于坐標軸（d、f、g軌道也如此），不管分子怎么轉它們的朝向都不會變。比如圖2所示，讓a狀態的氟代乙烯分子在YZ平面上旋轉，pz軌道的朝向將不變，為b情況，而不會成為c情況。

我們再來看看將乙烯進行旋轉后的高斯計算結果，如圖1下方所示。可以看到，π鍵照常形成，從圖上看與原先沒有任何差異，分子軌道能量也與原先一致。然而，組合系數卻發生了很大變化，原先只有px參與，現在px、py、pz都有很大程度的參與。這看起來很有趣，波函數組成看似不同，但結果完全一致。這并非偶然，而是必然，下面就來分析一下其原因。

將分子旋轉，可以看成是固定分子而旋轉坐標軸，已經提到，量化計算中原子軌道的朝向與坐標軸方向是“綁定”的，所以也就等于旋轉了原子軌道的朝向，將旋轉后得到的新朝向的三個p軌道叫做px'、py'、pz'，原先的朝向叫做px、py、pz。則px'可以寫為px、py、pz的線性組合，即px'=a*px+b*py+c*pz，py'、py'亦如此，當然px反過來也可以寫為px'、py'、pz'的線性組合。實際情況中，分子軌道顯然不只由px、py、pz軌道展開，可以進行推廣，將旋轉之前的基函數稱為a(i),i=1,2,3...；旋轉后的基函數稱為b(i),i=1,2,3...，也可以得到b(i)與a(i)的線性變換關系，b(i)=∑[k]X(k,i)a(k)（這里∑[k]代表令k=1,2,3...并將后面含k的項加和，后同），X就是變換矩陣，也就是b(i)在a(k)上的分量。

在旋轉前的a非正交基函數系下，求解正則Hartree-Fock方程就是已知F和S求解方程FC=SCE中的C和E。其中F為Fock矩陣，它正是Fock算符f在a基函數系下的矩陣形式，F(i,j)=<a(i)|f|a(j)>；S為重疊矩陣，S(i,j)=<a(i)|a(j)>；E為本征值矩陣，它是對角矩陣，對角元分別是每個分子軌道的能量；C為系數矩陣，C(i,j)為第j個分子軌道Ψ(j)在a(i)基函數上的展開系數，可寫成Ψ(j)=∑[i]C(i,j)a(i)。

令C=XC`，代入FC=SCE得FXC`=SXC`E，左右都乘上X'（后文都用X'代表X的共軛矩陣，A(i,j)"代表A(i,j)的共軛值），得X'FXC`=X'SXC`E。現在將X'FX進行轉化：
(X'FX)(i,j)=∑[k]X'(i,k)(FX)(k,j)=∑[k]X(k,i)"(FX)(k,j)=∑[k]X(k,i)"∑[l]F(k,l)X(l,j)=∑[k]∑[l]X(k,i)"X(l,j)<a(k)|f|a(l)>=<∑[k]X(k,i)a(k)|f|∑[l]X(l,j)a(l)>=<b(i)|f|b(j)>=F`(i,j)
即X'FX=F`。將Fock算符看成數字1，可以用同樣方法轉化X'SX成為S`，S(i,j)=<b(i)|f|b(j)>。這樣在基函數系a下求解FC=SCE就等價地轉化為了求解F`C`=S`C`E。從F`、S`的表達式可見，在旋轉后所得的b基函數系下求解正則HF方程，也正是求解F`C`=S`C`E。所以旋轉前后基函數雖變了，但求解的正則HF方程完全一樣，因此結果一模一樣，E矩陣不變故每條軌道能量不變，b基函數系下的C`和a下的基函數系C等價，所以描述的波函數不變。可以檢驗，例如b基函數系下解正則HF方程得到的Ψ(j)=∑[k]C`(k,j)b(k)，將b(k)=∑[l]X(l,k)a(l)代入，得∑[k]∑[l]C`(k,j)X(l,k)a(l)=∑[l](XC`)(l,j)a(l)=∑[l]C(l,j)a(l)=∑[k]C(k,j)a(k)，這正是在a基函數系下解正則HF方程得到的Ψ(j)。

顯然與波函數相關的分子的屬性也自然不會改變，比如軌道的圖形。所以只要兩套基函數之間能夠線性變換（但變換后的基不能有線性依賴）結果就完全一樣，這就是Hartree-Fock方法的線性變換不變性。旋轉不變性則是線性變換不變性的一個具體體現。還有很多的地方也利用了這種性質：量化計算中往往會將基組變換為最好用的基組，比如用群論方法簡化久期方程計算，就是將原子軌道基函數線性組合成含有對稱性信息的群軌道，使det(F-SE)行列式中很多要算的項直接化為0成為塊對角行列式來簡化求解。在實際求解HF方程中，也會先用正交化方法得出變換矩陣X使X'SX=I，FC=SCE就成為了FC=CE，即C^(-1)FC=E，求解C和E的問題就成了方法成熟的求解本征值和本征向量的問題。也可以先將原有原子軌道變換成軌道雜化再求解HF方程。

（半經驗方法常使用ZDO近似，因而重疊矩陣往往近似為單位矩陣，Fock矩陣中很多多中心雙電子積分項都成為了0，假設稱為矩陣K。此時方法不再具有基函數線性變換不變性，這與前面討論的HF方程的情況不同。一方面是S=I的近似明顯使上述推導不成立，因為不同基函數系下S顯然不同；另一方面，半經驗方法出于數值求解方便，根據ZDO近似對F進行不同程度的篡改，得到的K并不對應于某個算符，故K與K`不是同一個算符在不同表象下的矩陣形式，上述線性變換不變性的證明也不成立。但滿足線性變換不變性是重要的，尤其是要滿足其中同原子上基函數的線性變換不變性，否則將失去物理意義，所以很多半經驗方法通過將雙電子積分用預設參數取代，不僅加速了計算，也同時滿足了這個要求。比如使雙電子積分值不看軌道具體類型，只取決于所在中心，則雜化、旋轉引起的同原子上的基函數混合對結果將不產生影響。）

這樣我們就明白，旋轉分子不會令HF的能量、電子密度、分子軌道等改變，改變的只是量化程序輸出的分子軌道向各個原子軌道的展開系數。這就是說，量化程序中分子軌道如何由原子軌道組成，在某種意義上有任意成分，因為分子呈什么朝向完全是任意的，沒有對錯之分。這一點需要引起注意，例如有些人會以為，分子中形成大π鍵能從分子軌道組合系數中看出，一定幾乎只由某幾個原子的某種xyz標識相同的p軌道構成，實際上這是大誤。盡管往往程序根據對稱性自動調整分子的朝向，使得這個規律有時有效，比如對平面型分子，程序默認時會自動令分子平面與XY或XZ或YZ平面平行。

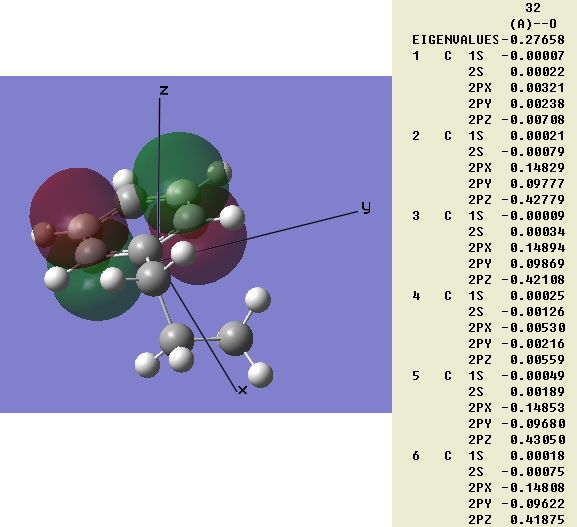
但即便允許程序自動調整分子朝向，這個規律也往往不符。例如我們用極小基計算丙基苯，沒有加nosymm關鍵字，允許程序自動調整分子位置和朝向。但是結果如圖3，自動設的朝向苯環平面就是傾斜的，常理上本應該純粹由pz軌道組成的兩個π鍵，從算出來的分子軌道組合系數上看是同一個原子上多個p原子軌道混合的。所以光從組成系數上分析而不看分子軌道圖形，憑人的直覺很難得出很多重要結論的，僅因為從分子軌道組合系數中看不出π鍵而對此體系亂下結論說不存在π鍵是大錯特錯。這樣的問題根源就是量化程序中根據坐標軸固定了原子軌道朝向而帶來的。還有人弄軌道成分分析程序，討論某某軌道由px、py、pz等原子軌道分別貢獻百分之多少，其實若初學者沒弄明白上述實質的話，是很容易得到錯誤結論的，分子一旋轉，軌道組成一下就變了，拿分子的某一種朝向計算結果來解釋不同xyz標識的原子軌道在分子中的功用，結果是沒意義的。

但是并不是說從程序輸出的分子軌道組合系數上不能獲得任何有用的信息。如果忽略重疊積分，我們可以用某個分子軌道上的每個原子軌道的系數的平方來近似估計原子軌道的貢獻。旋轉分子，也就是旋轉了分子軌道與原子軌道的相對朝向，雖會使它們的系數發生復雜的變化，但是這并不會使不同原子的軌道間發生混合，不會使不同類型（如p、d的）軌道發生混合，也不會使不同軌道指數的軌道發生混合。所以每個原子上軌道的總貢獻不會有變化，可以做出討論，也可以討論某個原子上哪幾類軌道貢獻對分子軌道貢獻較大，比如討論是2p、是3p還是3d或由幾類軌道共同貢獻等等，旋轉不會對它們貢獻的比例在本質上有影響，但是會對每一類當中有不同xyz標識的軌道的貢獻比例有著重大影響。所以我們可以考察分子軌道主要由哪些原子的哪種主量子數的哪種角量子數軌道貢獻，或者由哪個殼層的軌道貢獻，但絕對不能說比如某分子軌道就是由某原子px、py軌道貢獻，或者僅在闡述計算數據時在不引起歧義的情況下這么說，決不能把本來是任意的朝向問題帶入到結果的理論分析中。

我們有很多直覺性的化學鍵概念，這里最主要涉及的是π鍵概念，說它是純粹由p軌肩并肩組成，是因為我們總是將構成π鍵的原子軌道的朝向認為是垂直于相應部分的分子平面，分子旋轉一下，我們腦中的那個原子軌道的朝向也跟著轉，以保持它總是垂直于那個部分的分子平面。這顯然和原子軌道朝向“死板”的量子化學程序不符，人腦中的原子軌道朝向總是盡可能地調節以符合化學意義。比如兩個苯環由一個亞甲基相連，必然苯環平面之間是傾斜的，我們往往會想象苯環1上的所有碳的py軌道都垂直于苯環1的平面，苯環2上的所有碳的py軌道都垂直于苯環2的平面，在人腦中一個分子中甚至如此地構成了多個局部的坐標系。但是量化程序不懂這一套迎合人們化學直覺思維的表達方式，一刀切，為了方便，所有原子的py軌道必須平行于y軸，不管是什么分子。若程序經過內置算法自動調整方向后，恰好使原子軌道的朝向相對于分子的朝向符合人的習慣時，分子軌道組成系數看起來才舒服，此時π軌道從組合系數上看才僅由某幾個軌道構成。雖然前面已經提到，原子軌道朝向不改變分子屬性和波函數，但合適的朝向能方便人們從分子軌道組合系數中分析軌道如何由原子軌道構成，那程序何不加入這么個功能來討好用戶的直覺、迎合常規化學理念呢？這實在太麻煩，意義也不大，沒多少人關注這個小問題。