使用Multiwfn考察分子軌道、NBO等軌道對密度差、福井函數的貢獻

使用Multiwfn考察分子軌道、NBO等軌道對密度差、福井函數的貢獻

文/Sobereva@北京科音 2019-Aug-17

1 前言&基本知識

密度差是量子化學研究中經常被考察的量，Multiwfn可以非常容易地計算和繪制各種類型的密度差，見《使用Multiwfn作電子密度差圖》（http://www.shanxitv.org/113）。福井函數本質上也是密度差的一種，對于預測反應位點非常有實際價值，在http://bbs.keinsci.com/thread-384-1-1.html里有相關文章和我寫過的與福井函數有關的各種博文。

雖然對密度差直接作圖就可以考察密度差的基本特征來討論問題，但是如果能從軌道角度上討論密度差，或者說計算軌道對密度差的貢獻，對于更好地揭示密度差所體現的本質無疑是非常有益的。比如，因為電離過程會伴隨著軌道的弛豫，因此分子的垂直電離過程對應的密度差并不等同于HOMO軌道的概率密度（即HOMO波函數模的平方），但如果能考察各個軌道對密度差的貢獻，無疑可以得知哪個軌道是電離過程中最主要涉及的、其它軌道產生了多大影響。再比如，NBO軌道往往有明確化學意義，如果考察NBO軌道對福井函數的貢獻，相比于只去觀看福井函數的圖形，可以更充分、嚴格地解釋當前的福井函數的本質特征，進而討論各個鍵在反應過程中起到的角色。

軌道對密度差的貢獻并沒有唯一的計算方法。在J. Mol. Model., 24, 25 (2018)中，作者討論了NBO對福井函數的貢獻，給出了計算方法。但這篇文章寫得相當抽象，讀起來感覺也比較混亂。這篇文章還給出了一個叫UCA-FUKUI的程序來實現他們提出的算法，但我看過后感覺用起來相當麻煩。后來，我將JMM這篇文章的思想和算法充分做了廣義化并實現在了Multiwfn當中，使得Multiwfn可以非常方便地計算任意類型軌道（如MO、NBO、NAO、LMO、NTO等等）對任意類型密度差（如電子激發過程、電離過程、電子親合過程、加外電場前后）的貢獻。注意，這個功能從2019-Aug-9及之后更新的Multiwfn中才有。

Multiwfn的這個功能用的算法細節在相應版本手冊的3.200.13節里有非常詳細的介紹，因此本文就不細說了，只是簡單提一下梗概。大致思想就是密度差可以近似表達為各個軌道概率密度的線性組合，換句話說軌道的概率密度可以作為基近似地展開密度差，組合系數就是軌道對密度差的貢獻值，可正可負。各個軌道的概率密度乘上各自的貢獻值得到的函數下面被稱為fitted density。實際的密度差與fitted density的差異通過函數F體現，即這兩個函數的差值函數的平方在全空間的積分。通過最小二乘法令F對組合系數最小化就得到了軌道的貢獻值。

Multiwfn提供兩個指標衡量擬合誤差，一個是密度差與fitted density的差值的絕對值的全空間積分，在輸出信息里叫Fitting error (definition 1)。另一個就是擬合時用的F函數，在程序里叫Fitting error (definition 2)。

整個計算過程是基于立方格點實現的。具體來說，用戶需要給Multiwfn提供自己事先算好的密度差格點數據（通常用Multiwfn的主功能5產生cube文件），之后Multiwfn會自動計算各個格點上各個軌道的概率密度值，再根據擬合公式得到軌道貢獻值。顯然，納入考慮的軌道越多、格點數越高，整個計算過程耗時就會越高。

在使用最小二乘法的時候可以施加約束，要求所有軌道貢獻值加和等于特定值P，使得貢獻值更有化學意義或者令數量級更合理。比如如果密度差對應電子激發這種電子數不增不減的情況，可以讓P=0；對于福井函數f-的情況，由于是N電子態的密度減去N-1電子態的密度，可以讓P=1.0。如果不設定約束的時候算出來的貢獻值也合理，那么不施加約束也完全可以，擬合誤差還能因此更小一些。

這個算法雖然原本目是計算軌道對密度差的貢獻，但由于Multiwfn的這個功能非常靈活和普適，其實被擬合的函數并不要求非得是密度差，也可以是其它格點數據，比如特定情況下算出來的電子密度。

更多相關細節請參閱Multiwfn手冊3.200.13節，下面就直接通過幾個例子講解怎么實現分析。Multiwfn可以在官網http://www.shanxitv.org/multiwfn免費下載，相關基本知識見《Multiwfn FAQ》（http://www.shanxitv.org/452）。如果對Multiwfn可以支持的文件的特征和產生方法不了解，看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。

2 例子

2.1 計算分子軌道對苯酚的f-福井函數的貢獻

此例計算分子軌道對苯酚的f-福井函數的貢獻，這需要用到N電子態和N-1電子態的波函數文件，N代表苯酚中性時的電子數。這兩個態的文件phenol.wfn和phenol_N-1.wfn在程序包的examples目錄下已經提供了。怎么用Multiwfn計算福井函數在手冊4.5.4節已經寫得相當明白了，更多細節這里就不多提了。

計算分子軌道對f-的貢獻前我們需要先產生f-的格點文件。啟動Multiwfn然后輸入以下命令
examples\phenol.wfn
5 // 計算格點數據
0 // 自定義運算
1 // 有1個額外的文件將被納入相互運算
-,examples\phenol_N-1.wfn
1 // 被運算的函數是電子密度
2 // 中等質量格點（對于當前這種不大的體系，用這個檔次就足夠獲得可靠的貢獻值）
2 // 把算完的格點數據導出到當前目錄下的density.cub中

然后我們就可以開始計算軌道的貢獻了。當前我們只想考察中性狀態的苯酚的占據軌道對f-的貢獻，而一開始載入的phenol.wfn文件里包含的軌道正好就是這些軌道，所以我們直接按0退回到主菜單，輸入以下命令進行貢獻的計算
200 // 其它功能 (Part 2)
13 // 計算軌道對密度差或其它格點數據的貢獻。
density.cub // 即我們前面剛算出來的包含f-的cube文件
此時從屏幕上的選項1中，你會看到Multiwfn默認將所有軌道貢獻加和值約束為了1.0，這對于當前情況正合適。接著輸入
0 // 選擇軌道范圍并開始計算
o // 輸入字母o代表把所有占據數不為零的軌道作為擬合時被考慮的軌道，對于當前體系等價于把所有占據MO納入擬合來得到它們的貢獻

之后Multiwfn開始計算各個軌道的概率密度的格點數據，然后通過擬合得到貢獻值。輸出信息如下：
Orbital    20   Value:    -0.108
Orbital    11   Value:    -0.089
Orbital     9   Value:    -0.065
Orbital    10   Value:    -0.061
Orbital     8   Value:    -0.044
Orbital    14   Value:    -0.030
Orbital    19   Value:    -0.004
Orbital    15   Value:    -0.002
Orbital     7   Value:    -0.001
Orbital    17   Value:    -0.001
Orbital     1   Value:    -0.001
Orbital     6   Value:    -0.001
Orbital     2   Value:    -0.001
Orbital     3   Value:    -0.000
Orbital     5   Value:    -0.000
Orbital     4   Value:     0.000
Orbital    16   Value:     0.022
Orbital    12   Value:     0.030
Orbital    18   Value:     0.052
Orbital    13   Value:     0.055
Orbital    21   Value:     0.064
Orbital    22   Value:     0.095
Orbital    23   Value:     0.111
Orbital    24   Value:     0.214
Orbital    25   Value:     0.766
Sum of all values:       1.000
Fitting error (definition 1):      0.8911
Fitting error (definition 2):    0.003828

上面的Value就是貢獻值。可見MO25，即HOMO，對f-有絕對主導性的貢獻，其貢獻值0.766遠大于其它的。但由于也有幾個其它軌道貢獻值并不可忽略，比如MO24和MO23分別是0.214和0.111，這說明f-雖然可以定性正確被HOMO對應的概率密度所表現，但差異還是不容忽視的。MO20、MO11等幾個軌道的貢獻值為負，這暗示f-也存在數值為負的區域，眾所周知這是由軌道弛豫效應所導致的。

現在在屏幕上可以看到一個菜單，可以用相應選項顯示你提供的格點數據（即f-）的等值面、擬合出的格點數據的等值面（即前文說的fitted density），以及二者的差值函數的等值面。這幾個格點數據的0.005等值面，以及前面提到的幾個軌道的0.07等值面如下所示

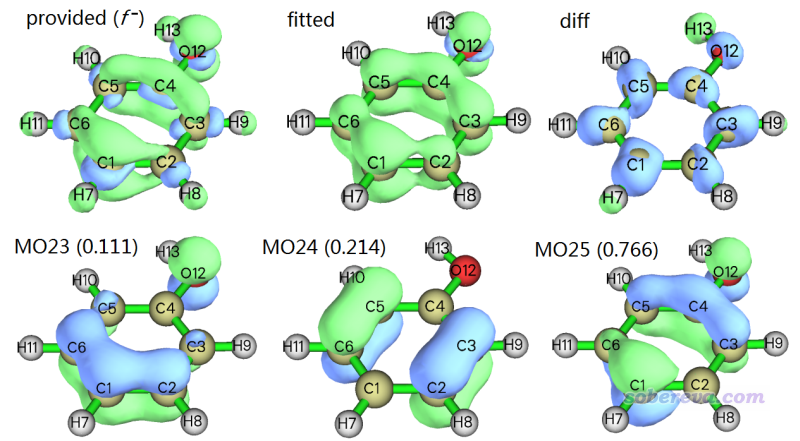
由圖可見擬合出來的格點數據等值面和f-等值面定性一致，至少在pi區域高度相符，所以當前做的擬合是有意義的。但是這倆等值面在sigma電子出現的區域有顯著差別，差值函數（diff）的圖充分體現出了這一點。這部分特征雖然沒擬合好，但這不是什么重點，因為對當前體系的f-主要用來考察pi區域的親電反應情況。
PS：如果你去看一下那些貢獻值為負的軌道，比如MO20，會發現這些軌道是sigma軌道。但由于它們的形狀都與diff的特征偏離較大，所以把這些sigma軌道引入擬合中也并沒有改善這部分區域的擬合質量。

從上圖也可看到，MO25的形狀和f-在pi區域比較相似，也因此MO25是f-的主要貢獻者，貢獻值最大。對于討論親電反應位點，在原理上，用f-討論比前線軌道理論(FMO)主張的用HOMO分布討論要嚴格得多，但從實用角度來講考察HOMO依然往往能說明問題，這從當前體系HOMO可以定性正確表現f-的特征上就可以看出來。若f-恰好等于HOMO的分布，那么就只有HOMO的貢獻為1.0，而其它軌道的貢獻都為0.0，因此我們可以用最大軌道貢獻值與1.0的差值來衡量當前情況下FMO理論的適用程度。當偏差特別大的情況顯然光靠分析一個軌道是不足以可靠地說明反應位點的。

2.2 計算NBO軌道對1,3-丁二烯福井函數f-的貢獻

這次我們考察NBO軌道對1,3-丁二烯福井函數f-的貢獻。相關文件都在examples\orb_densdiff\butadiene里提供了。做這個計算，我們必須得向Multiwfn提供記錄了NBO軌道的文件，通常都是使用NBO plot文件，通過其中的.31和.37文件Multiwfn就可以分析NBO軌道了，關于這點詳見《使用Multiwfn繪制NBO及相關軌道》（http://www.shanxitv.org/134）。

啟動Multiwfn，然后依次輸入
examples\orb_densdiff\butadiene\butadiene.fch // 中性狀態的丁二烯
5 // 計算格點數據
0 // 自定義運算
1 // 有1個文件將被納入相互運算
-,examples\orb_densdiff\butadiene\butadiene_N-1.fch // N-1電子態的丁二烯
1 // 被運算的函數是電子密度
2 // 低質量格點（由于當前體系很小，基于格點數較低的格點設定算出來的軌道貢獻值就足夠準確）
2 // 把算完的格點數據導出到當前目錄下的density.cub中

重啟Multiwfn，然后輸入
examples\orb_densdiff\butadiene\BUTADIENE.31 // 此文件包含基函數定義
37 // 載入當前目錄下的BUTADIENE.37，其中含有NBO軌道展開系數信息
我們當前只想考察高占據的NBO軌道（也叫做Lewis型NBO軌道）對f-的貢獻。大家自己去看NBO模塊的輸出信息可以判斷這些軌道的序號范圍，也可以進入Multiwfn的主功能6，用選項3來顯示出各個軌道的占據數。你會發現前15個軌道都是高占據的，接近2.0，因此我們要把它們納入擬合。在Multiwfn主菜單里接著輸入
200 // 其它功能 (Part 2)
13 // 計算軌道對密度差或其它格點數據的貢獻
density.cub // 即我們前面剛算出來的包含f-的cube文件
0 // 選擇軌道范圍并開始計算
1-15 // Lewis型NBO軌道的序號范圍

此時看到以下信息
Orbital     3   Value:    -0.047
Orbital     8   Value:    -0.046
[略...]
Orbital    10   Value:     0.017
Orbital     4   Value:     0.530
Orbital     9   Value:     0.531
Sum of all values:       1.000
Fitting error (definition 1):      0.9008
Fitting error (definition 2):    0.004961

可見NBO4和NBO9一起主導f-，二者貢獻相同。下面是實際的f-、擬合出的f-的0.01等值面，以及NBO4和NBO9的0.1等值面。

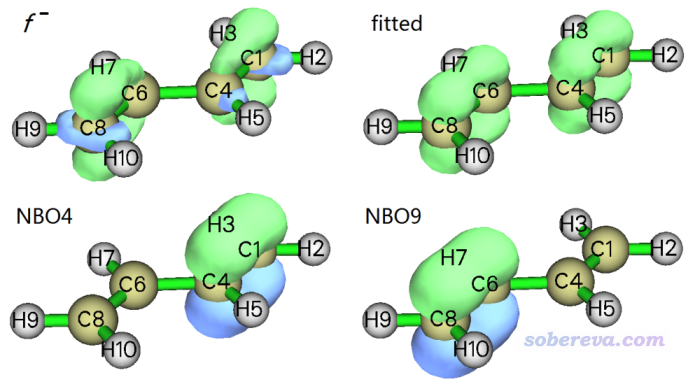
由上圖可見擬合出的f-和實際的f-非常相符，都是主要分布在兩個邊緣的C-C鍵的pi區域。從NBO軌道的貢獻值以及軌道圖形來看，可以視為f-主要是邊緣兩個C-C鍵的pi軌道貢獻的。

2.3 計算NBO軌道對甲醛的S0->S1密度差的貢獻

這一節我們考察甲醛的各個NBO軌道對S0態垂直躍遷到S1態對應的密度差的貢獻。examples\orb_densdiff\H2CO目錄下的S0.fch是對S0態優化好的甲醛在B3LYP/6-31G*下算單點得到的文件，順帶還產生了此目錄下的NBO plot文件。S1.wfn是對S0極小點結構下用B3LYP/6-31G*做TDDFT得到的S1態的.wfn文件。相應任務的gjf文件已經直接提供在此目錄下了。如果缺乏電子激發計算的相關知識，看《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》（http://www.shanxitv.org/314）。

首先生成S0->S1躍遷對應的密度差，即S1的密度減S0的密度。啟動Multiwfn然后輸入
5 // 計算格點數據
0 // 自定義運算
1 // 有1個文件將納入相互運算
-,examples\orb_densdiff\H2CO\S0.fch
1 // 電子密度
1 // 低質量格點
2 // 把算完的格點數據導出到當前目錄下的density.cub中

現在我們也可以選擇選項-1直接看一下密度差格點數據，如下所示（等值面=0.03）

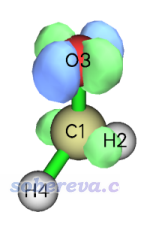
其實從這個等值面圖我們就已經可以大致判斷出這個躍遷的特征了。相關討論見《圖解電子激發的分類》（http://www.shanxitv.org/284）。但這里我們從軌道角度對其特征進行更嚴格的討論。重啟Multiwfn然后輸入
examples\orb_densdiff\H2CO\H2CO.31
37 // 載入相同目錄下的同名的.37文件，里面包含NBO軌道信息
200 // 其它功能 (Part 2)
13 // 計算軌道對密度差或其它格點數據的貢獻
density.cub // 前面我們算出來的S0->S1密度差的格點數據
1 // 設置對貢獻加和值的約束
2 // 設為指定值
0 // 將貢獻加和值約束為0。因為電子激發前后電子數沒有變，因此強制令貢獻加和值為0是有依據的
0 // 選擇軌道并開始分析
然后直接按回車，代表把所有軌道都納入考慮。之所以這里我們不再像前例一樣只考慮高占據的NBO，是因為電子激發過程可以表述為各種占據軌道向各種空軌道的躍遷的組合，因此占據數近乎為0的NBO也應當納入分析。輸出的信息如下：

Orbital     8   Value:    -0.719
Orbital    16   Value:    -0.254
Orbital     9   Value:    -0.151
[略...]
Orbital    11   Value:     0.115
Orbital    22   Value:     0.132
Orbital    18   Value:     0.148
Orbital    32   Value:     0.894
Sum of all values:       0.000
Fitting error (definition 1):      0.4778
Fitting error (definition 2):    0.001770

可見貢獻最正的是NBO32，貢獻最負的是NBO8。其它軌道也有一定參與，但如果我們只想考察主體特征，可以暫且忽略它們。從S0態計算的輸出文件examples\orb_densdiff\H2CO\S0.out中的NBO分析部分，我們可以看到這程序自動對兩個軌道做的標記，后面的數值是占據數：
8. LP ( 2) O 3 1.88565
32. BD*( 1) C 1 - O 3 0.00000

可見NBO8是O3的孤對電子軌道，而NBO32的特征從上述信息尚不好判斷，我們可以結合其等值面圖考察。擬合出的密度差的0.03等值面圖，以及這兩個NBO軌道的0.17等值面圖如下所示

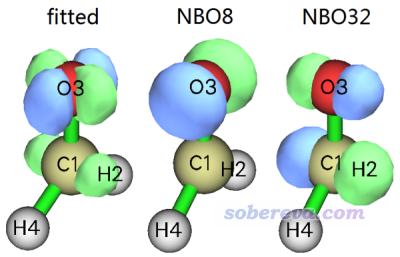
從軌道圖形可以判斷NBO32是C1-O3的反pi軌道。再結合Multiwfn計算出的NBO貢獻值，我們可以很嚴格地將S0->S1指認為是n(O3)->*(C1-O3)型的躍遷。另外，上圖中擬合出的密度差與前面給出的實際的密度差極其相似，肉眼很難看出差別，這也體現出當前擬合質量非常高，也因此得到的軌道對密度差的貢獻值在解釋密度差本質特征上是很可靠的。

在examples\orb_densdiff\H2CO\目錄下還有個H2CO.33，這是記錄NAO軌道的文件。如果你想考察NAO對密度差的貢獻，只需要在載入.37文件的那一步改成載入.33文件即可，之后的操作完全相同，感興趣的讀者可以一試。

3 總結

本文介紹的Multiwfn計算軌道對密度差（或其它格點數據）貢獻的功能非常普適，能做的分析遠不僅本文示例所展示的。本文只用了很簡單體系做了示例，希望讀者能結合上面的例子充分理解這個功能的思想、用法，并弄清楚算法特點，從而靈活、恰當地運用此功能研究各種實際問題。