談談勢能面交叉對激發態優化的影響
談談勢能面交叉對激發態優化的影響
文/Sobereva@北京科音 2019-Mar-2
0 前言
TDDFT是目前最常用的激發態計算方法,以前在計算化學公社論壇上有很多次有人問為什么用Gaussian結合TDDFT優化的時候激發態順序變化了、優化出來的激發態不是自己一開始要求的那個激發態之類的問題,這其實都是由于激發態勢能面交叉所致,在本文就專門說一下這個問題。筆者假定讀者已經閱讀過這些文章了解了相關基礎知識:《圖解電子激發的分類》(http://www.shanxitv.org/284)、《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》(http://www.shanxitv.org/314)。看一下《使用sobMECP程序結合Gaussian程序搜索極小能量交叉點》(http://www.shanxitv.org/286)對理解本文提到的一些概念也有幫助。本文用的Gaussian是G16 A.03版,軌道圖形繪制和NTO分析都是Multiwfn 3.6(dev)做的。
1 透熱態與絕熱態
在討論激發態優化之前,首先要弄清楚透熱態和絕熱態的概念,看下圖
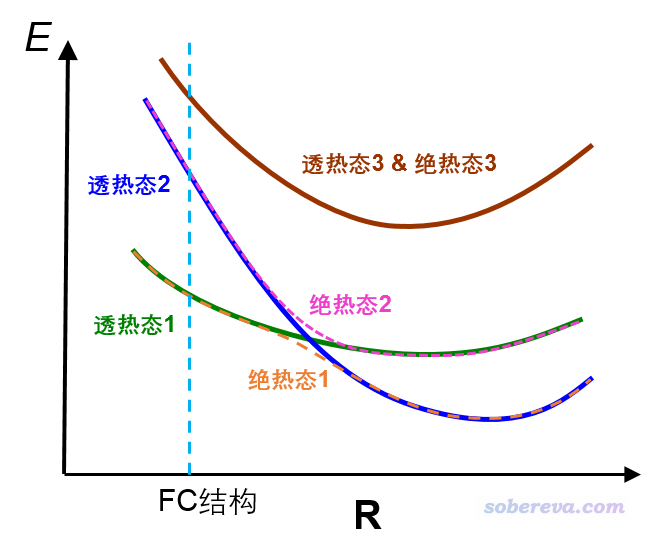
圖中的態都是激發態,為了便于討論假定都是單重態。FC結構指的是基態極小點結構。圖中綠線和藍線分別對應兩個透熱態勢能面,可以認為每個透熱態對應一種特定的電子激發模式,比如可以假設透熱態1對應n->pi*激發,透熱態2對應pi->pi*激發。當兩個透熱態能量相近時,由于態與態之間在一般會存在耦合(體現在相應的哈密頓矩陣非對角元不為0),兩個透熱態的波函數會混合產生出兩個絕熱態,對應不同絕熱態勢能面,在原本兩個透熱態相交的位置存在能量分裂。至于圖上的棕色曲線,由于在圖中的幾何結構下與其它激發態勢能面較遠,因此既是透熱態也是絕熱態。
對于激發態優化過程中經歷透熱態交叉區域的情況,常用的S1、S2...這種稱呼就具有含糊性了,必須得說清楚。如果你說的是透熱態,那么按照能量由低到高編號的時候,得說清楚是對于什么結構而言的。比如上圖中,在交叉點左邊區域的S1(綠色曲線)到了交叉點右邊就是第二激發態了,如果重新按照激發能排序,它就應該被稱為S2了。而如果你討論的是絕熱態,按照絕熱態能量由低到高來稱呼S1、S2...,那就沒有這個問題,比如圖中的粉色虛線在各個位置下都是能量第二高的激發態。
2 牽扯勢能面交叉時的激發態的幾何優化
做激發態優化時,每一步都會算出一批激發態,那么怎么確定應當按照哪個激發態來優化?換句話說,應當在當前結構下對哪個激發態計算受力/Hessian來獲得下一步的結構?不同程序有不同做法。Gaussian等一些程序的做法是根據組態系數,比較當前步算出來的各個激發態與上一步算出來的激發態的對應關系。比如上一步的時候感興趣的態是能量第三低的態(i態),因此上一步的時候受力/Hessian也是對這個態來算的,而在當前結構下,若發現能量第二低的態(j態)的波函數與上一步的i態最接近,那么上一步的i態就與這一步的j態產生了映射(map)關系,因此當前這一步感興趣的態就是j態,計算接下來的位移所需的受力/Hessian也是對j態來算的。通過這種方法,Gaussian實現了所謂的state-tracking(態的跟蹤)。
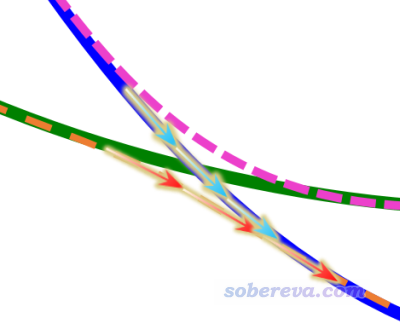
上面這種做法對于被優化的態不牽扯勢能面交叉的情況完全穩妥(比如上圖中棕線所示的第三激發態),但是當牽扯勢能面交叉時,就有一些復雜情況了,見下圖

上圖體現從FC結構出發,優化FC結構下的第一激發態的過程。在當前結構逐漸移動到透熱態交叉點附近時,接下來既可能沿著綠色箭頭的方向走,從而最終優化到一開始所處的透熱態勢能面極小點上;也可能按照紅色箭頭走,最終優化到第一絕熱態勢能面的極小點上。根據Gaussian的state-tracking思想,由于沿著透熱態優化每一步波函數特征改變較小,因此一般是沿著透熱態勢能面優化的。但是,也有時候,由于判斷算法的不可靠或者一些數值因素,最終也可能會被優化到第一絕熱態極小點去。究竟會出現哪種情況,有很大的運氣因素,比如把步長上限改一下,或者用不同基組/泛函,最終就可能會被優化到不同的極小點去。因此得理清思路,搞明白到底出現了什么情況。
我們知道,在Gaussian的TDDFT計算時,我們可以通過root=i指定優化第i激發態。更確切來說,被優化的是在初始結構下按照能量排序的第i透熱態(當然,由于Gaussian的state-tracking算法的不足,因此實際優化的結果并不一定是如我們所愿的那樣)。由于可能優化過程中經歷勢能面交叉區域,因此通過root=i關鍵詞試圖優化第i激發態的時候,顯然不能讓總共被算出來的激發態數(nstates)也恰好等于i,否則可能當這個態與更高激發態出現交叉時導致跟蹤透熱態失敗。筆者建議nstates設i+2或稍微更多一些。而且,就算是為了保證算出來的激發態本身比較準確,nstates也不應該正好頂著感興趣的態來設,這在《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》一文中已經提過了。
對于很多體系,激發態,尤其是高階的激發態能級分布特別密集,即有大量激發態勢能面彼此十分接近。這個時候,你若想要求Gaussian優化你一開始用root關鍵詞選定的態并一直在其透熱勢能面上行進,那真正達到目的幾率可能較低,因為如前所述,很可能中途因為走上了絕熱態的路徑(某種意義上,類似于發生了內轉換),結果最終跑到不是你真正感興趣的透熱態極小點上。
還有一種情況,是一開始用root指定優化不同的激發態,發現最終優化出的結果都一樣,也是因為勢能面交叉,并且Gaussian的state-tracking算法有所不足導致沒法保證跟蹤透熱態所致,如下圖示例的,可能一開始用root=1和root=2做優化,最后發現都優化到了第一絕熱態極小點了。
3 SDNTO算法
2019年初在JCC上出了一篇文章(DOI: 10.1002/jcc.25800),提出了一種新方法來實現state-tracking,是基于當前步與上一步產生的NTO來比較當前步算出的各個態與上一步的時候被跟蹤的態的重疊程度,重疊程度最大者就是這一步應當被跟蹤的態。如果你不懂NTO,參看《使用Multiwfn做自然躍遷軌道(NTO)分析》(http://www.shanxitv.org/377)。重疊程度計算方式如下
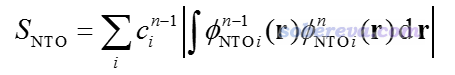
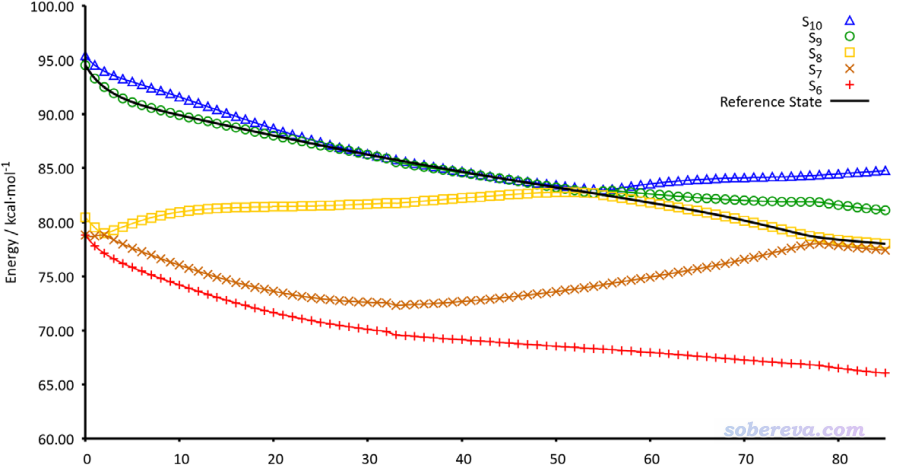
其中n是當前步,n-1是上一步,φ是NTO軌道波函數,c是NTO的本征值,只有大于人為設定的閾值的NTO才納入上述加和。文中基于這種思想,結合很簡單的最陡下降法,提出了所謂的Steepest Descent minimization using Natural Transition Orbitals (SDNTO)方法來試圖確保在優化中能夠跟蹤透熱態。實測發現,即便對于激發態能級很密集的配合物,這種算法也能成功跟蹤一開始指定的透熱態。下圖是SDNTO文章中通過SDNTO算法優化cis-(Cl,Cl)[RuCl2(NO)(tpy)]+配合物的第9透熱態的過程,橫坐標是優化的步數,圖中不同顏色表示每一步結構下的不同的絕熱態激發能。可見對于這樣勢能面交叉復雜的情況,SDNTO方法也很好地跟蹤了指定的透熱態,而原文說Gaussian自己的算法對此體系是失敗的。
SDNTO這種算法目前沒有公開的程序實現,作者自己的程序也是通過外掛Gaussian實現的,究竟SDNTO算法是否普適、效果好壞是否嚴重依賴于人為設定的參數,那還是未知數。順帶一提,如果你想計算兩個結構中的各個軌道間的重疊積分的話,用Multiwfn就可以輕易實現,有專門的功能,看Multiwfn手冊3.200.6節的例子。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載。由于Multiwfn有這個功能,再加上Multiwfn可以直接產生記錄了NTO軌道的fch文件,其實借助Multiwfn自己寫一個基于Gaussian實現SDNTO優化的程序也并不復雜。不排除可能在以后的Gaussian中會直接支持SDNTO方法。
4 涉及激發態勢能面交叉的Gaussian TDDFT優化一例:胞嘧啶
胞嘧啶(cytosine)這個體系在SDNTO文章中做了研究,文中提到在距離FC結構很近的地方就有S1和S2間的圓錐交叉。這里我們用Gaussian實際做一下TDDFT對S1和S2的優化,看看是什么情況(筆者算出來的結果和SDNTO文章所述的有所出入,下文根據實際算出來的情況說事)。計算涉及的輸入輸出文件都可以在這里下載:http://www.shanxitv.org/attach/468/file.rar。初始結構是PBE0/6-31G*優化的基態結構,為穩妥起見激發態計算都是設nstates=5。為了與SDNTO文章一致,激發態計算用的是PBE0/6-31+G*。
Gaussian的TDDFT優化的每一步都會輸出當前結構下所有激發態信息,輸出文件里會看到“Excited State 1:"、“Excited State 2:"等等。此處Excited State x相當于在當前結構下,被Gaussian判斷為與初始結構下第x態相映射的態(即對應同一個透熱態)。當然,Gaussian判斷得是否合理那不一定。
4.1 默認步長下優化S1
我們先來優化S1,這里用默認步長,輸入文件是文件包里的S1_defstep.gjf。當前我們設的是root=1,因此,每一步中被Gaussian標記成"Excited State 1"的態就是被優化的態,每一步的受力/Hessian都是對當前被標記成"Excited State 1"態來計算的。
把.out文件中所有含有"Excited State 1"和"Excited State 2"的行里面的激發能提取出來,繪制成激發能隨優化步數的變化,得到的圖如下所示。為了把細節看得清楚,圖中只展現了前12步
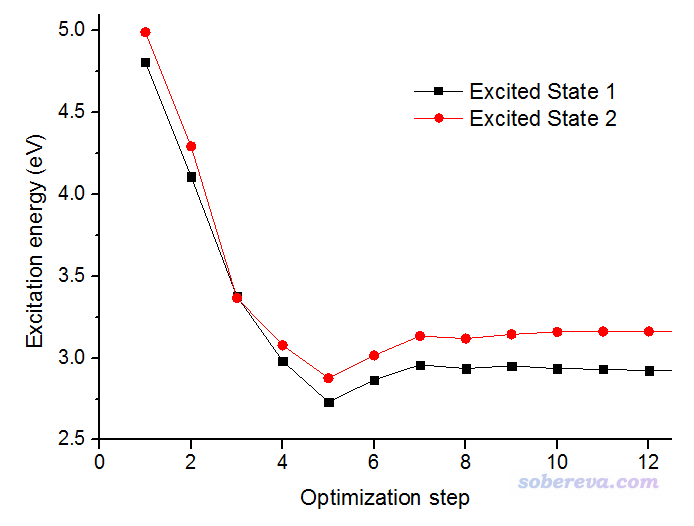
由圖可見,在第3步的時候兩個激發態能量幾乎相同,明顯出現了交叉。當前優化過程在經過交叉點時并沒有理應地在透熱態勢能面上進行,而是最終走了絕熱態的勢能面,也即對應"Excited State 1"的黑色曲線在交叉點右側都是能量最低的,這可以算是體現了Gaussian的state-tracking算法的失敗。
由于當前沒有一直在最開始的S1透熱態上走,而是中途切換到了S2的透熱態去,因此,優化第一步的"Excited State 1"的電子激發特征和最終結構的"Excited State 1"的電子激發特征必然不相符。為了更好地說明這一點,我們下面通過軌道考察一下電子激發特征。
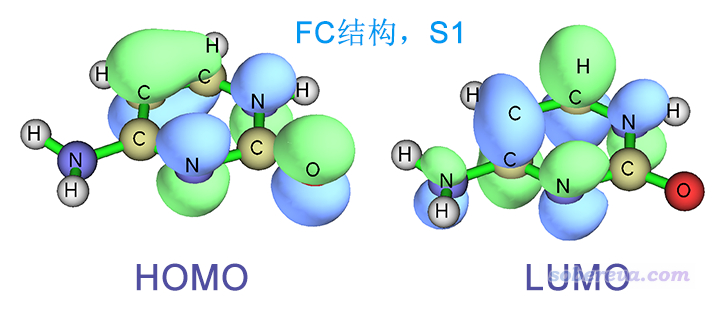
FC結構下S0->S1的躍遷幾乎完全對應HOMO->LUMO躍遷,兩個軌道圖形如下,可見是pi->pi*躍遷。
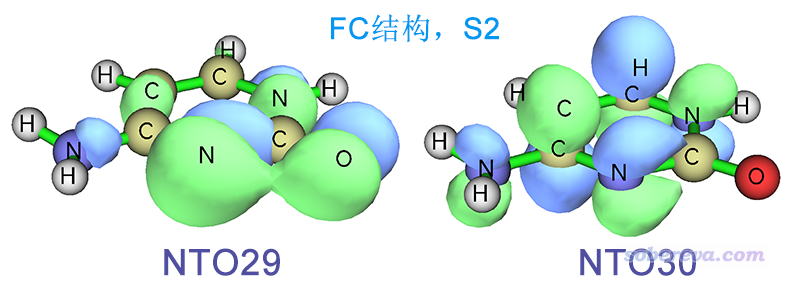
FC結構下S0->S2的躍遷缺乏主導的MO躍遷,因此使用Multiwfn轉化為NTO躍遷的方式描述,可幾乎完美地表示為NTO29->NTO30,由下圖可見是n->pi*躍遷,而且孤對電子同時明顯來自N和O。
下圖是在我們剛才做S1優化得到的結構下"Excited State 1"的躍遷方式,可以用NTO29->NTO30完美描述,可見明顯是n->pi*躍遷。
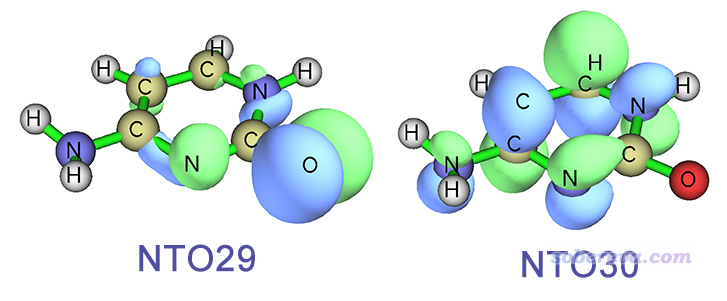
一對照就看出,我們所優化的出態,也就是被Gaussian標記為"Excited State 1"的態,其實對應的是FC結構下的S2透熱態,優化過程并沒有從始至終一直在S1透熱態上走。
4.2 在較小步長上限下優化S1
我們再來看看如果把步長上限設得很小,即使用opt(maxstep=3,notrust),從FC結構出發優化S1態是什么情況。輸入文件是文件包里的S1_step3.gjf
還是把輸出文件中含有"Excited State 1"和"Excited State 2"的行里面的激發能都提取出來并繪制,得到的圖如下所示。
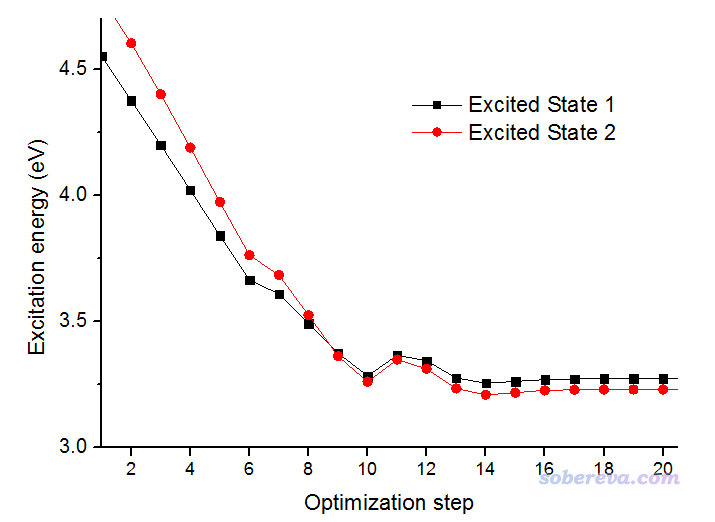
從圖上可以看出這回確實是走了透熱態的路徑,優化經過第9步結構附近的交叉點后,對應"Excited State 1"的黑色曲線就不再是能量最低的態了。這張圖里的交叉點位置和上一張圖里的交叉點位置基本相同,都是3.37eV的地方。
下面是優化過程第一步輸出的信息
Excited State 1: Singlet-A 4.8092 eV 257.81 nm f=0.0488 <S**2>=0.000
29 -> 30 0.69464
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-DFT) = -394.332374034
Copying the excited state density for this state as the 1-particle RhoCI density.
Excited State 2: Singlet-A 4.9900 eV 248.47 nm f=0.0019 <S**2>=0.000
26 -> 30 -0.32031
27 -> 30 -0.20046
28 -> 30 0.59079
Excited State 3: Singlet-A 5.3909 eV 229.99 nm f=0.0006 <S**2>=0.000
26 -> 30 0.61783
27 -> 30 -0.15704
28 -> 30 0.28651
...略
下面是優化過程最后一步輸出的信息
Excited State 1: Singlet-A 3.2680 eV 379.39 nm f=0.0122 <S**2>=0.000
29 -> 30 -0.70445
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-DFT) = -394.357141147
Copying the excited state density for this state as the 1-particle RhoCI density.
Excited State 2: Singlet-A 3.2250 eV 384.45 nm f=0.0000 <S**2>=0.000
28 -> 30 0.70662
Excited State 3: Singlet-A 4.5729 eV 271.13 nm f=0.0024 <S**2>=0.000
26 -> 30 -0.69564
27 -> 30 -0.10455
...略
由于"This state for optimization and/or second-order correction"是對"Excited State 1"標注的,因此程序是對"Excited State 1"來計算受力/Hessian從而優化結構的(當然這是必然的,因為我們設的就是root=1)。
由以上信息可見,程序輸出的時候總是按照Excited State 1,2,3,4...這樣的次序輸出的,但由于中途經歷了勢能面交叉,而且這次又成功地跟蹤了S1透熱態,因此到最后的結構下,被優化的對象"Excited State 1"的激發能已經變得高于"Excited State 2"了。另外,如組態系數體現的,"Excited State 1"是MO29->MO30躍遷,即HOMO->LUMO躍遷,如果你看一下這個結構下的這倆軌道的話,會發現這倆軌道都是pi軌道,這點也和FC結構下S1是pi-pi*躍遷完全對應。
在實際中,并非碰上沒有順利跟蹤透熱態的時候用小步長上限就總能解決問題,有的時候由于巧合,可能小步長上限的時候在交叉點附近誤走上了絕熱態,而用默認步長上限時反倒正確跟蹤了透熱態。
上一節我們原本想優化到S1透熱態極小點,卻“誤”被優化到了第一絕熱態極小點上,實際上也可以嘗試補救,也就是在這個第一絕熱態極小點上用TD(root=2)去優化在當前結構下應當是第2激發態的S1透熱態。這個任務的輸出文件是文件包里的S1_reopt.out,可以看到重新優化后,確實得到了S1透熱態極小點,結構與本節我們得到的完全相同。
4.3 對S2的優化
再來看看對胞嘧啶的S2優化的情況。我們以FC結構作為起點,使用opt(maxstep=3,notrust) TD(nstates=5,root=2)關鍵詞來做,計算級別同前。輸入文件是文件包里的S2_step3.gjf。
還是將優化過程的"Excited State 1"和"Excited State 2"的激發能隨優化步數的變化作圖,如下所示
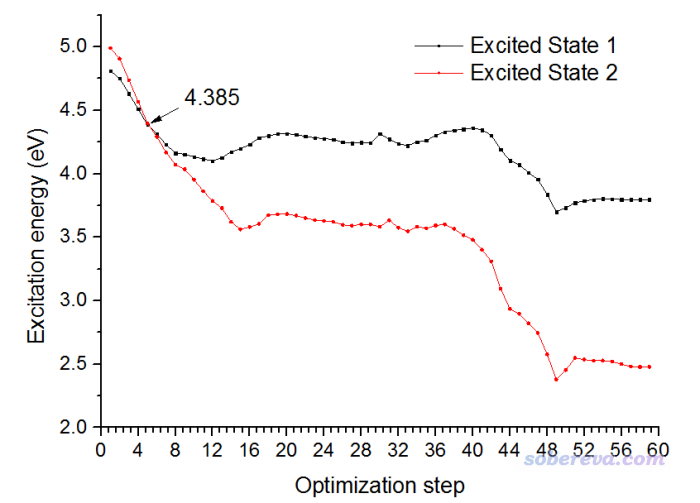
可見這次優化也經歷了交叉點,是沿著S2透熱態走的,因此紅線在一開始是能量第二低的態,到了交叉點右側就變成了能量最低的態了。但是,這次經歷的交叉點和上一節的是不同,這次交叉點的位置是大約4.385 eV的位置,而之前經歷的都是3.37eV的位置。為何會有區別?實際上S1和S2透熱態之間的交叉實際上是個交叉縫(在一個高維空間內處處能量相同),有無數多個相交的位置,由于上一節的優化一開始是按照S1透熱態的受力/Hessian移動的結構,而這一節是按照S2透熱態的受力/Hessian進行的移動,因此經歷了交叉縫的不同位置。
上一節兩個任務優化出的結構,以及這一節優化出的最終結構(都無虛頻)是各不相同的,結構如下

可見當前我們直接優化S2得到的最終結構相當扭曲,在這個結構下,這個態可以用NTO29->NTO30完美描述,這倆軌道如下所示
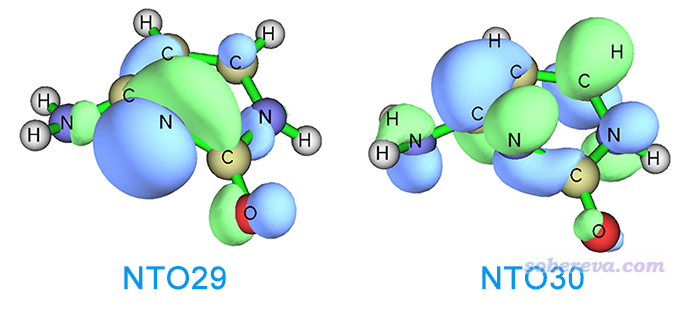
可見這個躍遷是n->pi*躍遷,如前所述這也正是FC結構下S2態的躍遷方式,進一步表明我們這一節的優化從始至終是在S2透熱勢能面上進行的。
由于S1和S2的交叉縫是高維的,因此從FC結構開始,沿著S1透熱態的受力/Hessian行進,以及按照S2透熱態的受力/Hessian行進,我們經歷了不同的交叉點位置。而且又由于此體系S2透熱態上有不同的極小點,因此本節一直沿著S2透熱態走(稱為a過程),以及上一節起初沿著S1透熱態走但是中途因算法問題在交叉點處切換到了S2透熱態(稱為b過程),最終得到的兩個S2透熱態極小點結構是不同的。根據之前給出的NTO圖,可以知道FC結構下的S2對應的n->pi*躍遷中孤對電子同時明顯來自于O和N,而a過程最終優化出的是n(N)->pi*態的極小點,b過程則優化出的是n(O)->pi*態的極小點。
另外,如果本節在優化S2時用默認步長上限,我們會發現優化出的結構和用maxstep=3的時候略有不同(輸出文件是文件包里的S2_defstep.out),不過差異非常小,對應于由于NH2朝向的不同所造成的兩個特征很接近的n(N)->pi*躍遷的極小點。之所以步長上限的不同導致了優化出了這兩個不同結構,必定是S2透熱態勢能面存在分叉,步長上限不同時由于巧合而恰好走了不同路徑。有興趣的讀者可以在gview里打開S2_step3.out和S2_defstep.out仔細對比一下優化過程。
5 總結
激發態的優化比基態的優化復雜很多。由于激發態能級分布密集,優化過程經常經過勢能面交叉區域,而且既有可能走透熱路徑也有可能走絕熱路徑,再加上激發態勢能面又可能分叉、聯通不同極小點,因此不光是計算級別會影響最終得到的結果,就連一些細碎的數值方面的設定諸如步長上限的差異都可能導致最終優化到不同結構上去,因此頭腦里必須有清楚的勢能面的概念、有對勢能面交叉問題的正確理解。如果能把本文的胞嘧啶這個簡單例子里的討論、分析方法都徹底弄明白,對其它更復雜的體系優化激發態時若遇到一些令人困惑的結果,也應該不難搞清楚到底是怎么回事了。