使用KiSThelP結合Gaussian基于過渡態理論計算反應速率常數
后記:對于計算反應速率常數,如果沒有特別的要求,實際上通過《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552)里介紹的我開發的Shermo程序計算出過渡態、反應物的自由能,求差得到自由能壘,然后代入我制作的《基于過渡態理論計算反應速率常數的Excel表格》(http://www.shanxitv.org/310)表格中,并且利用表格里的單元格計算出隧道效應校正量,就足矣得到合理的反應速率常數。如今并沒有多大必要用KiSThelP,用這個反倒還更復雜,還得裝java運行環境,從結果上看也沒什么特別顯著的額外好處。而且Shermo程序在計算熱力學量方面明顯比KiSThelP強大靈活得多。
使用KiSThelP結合Gaussian基于過渡態理論計算反應速率常數
文/Sobereva @北京科音
First release: 2014-Jul-28 Last update: 2021-Feb-27
1 前言
計算基元反應的反應速率常數k是一個很重要的和實際應用密切相關的問題。常見的計算方法包括硬球碰撞模型、軌跡計算、過渡態理論以及RRKM理論。硬球碰撞模型雖然有重要的歷史意義和理論意義,但精度太差,還需要額外的參數,沒什么實際價值,但天朝的物理化學課程中通常都喜歡細講這部分。軌跡計算就是通過從頭算動力學(如BOMD、CPMD,甚至高大上的量子動力學)計算大量的軌跡,讓分子或原子以不同動能、角度相互碰撞,看是否發生反應,將結果根據玻爾茲曼分布平均起來就能得到反應速率常數。這種方式最精確、最普適,但極為耗時、不易實現,日常問題研究中比較少用。RRKM算得挺準,但最大限制是只能用于單分子反應,諸如分子異構化等。過渡態理論(TST)是應用得最為廣泛的計算反應速率常數的方法,它假定反應物由于與環境的能量快速交換而處于熱力學平衡狀態,其中分布于過渡態(連接反應物和產物的IRC上能量最大點)的反應物就會轉化成產物。TST最初1935年Eyring等人提出后又有了發展,特別是變分過渡態理論(VTST),其中包括CVT(Canonical variational theory)、ICVT(Improved canonical variational theory)、μVT(Microcanonical variational theory)。CVT使用最廣,需要的勢能面信息最少,同時相對來說也是VTST里面精度最低的,但好于原始的TST(特別是電子能量對能壘貢獻很小甚至為0的情況,TST就很不合適了)。隧道效應對反應速率常數往往有不小影響,會增大k值,通常會計算出透射系數χ(有多種方式計算,準確度和計算難度直接相關),把它乘到過渡態理論得到的k上就得到了隧道效應校正后的結果(透射系數作為一個k的校正因子,也能夠引入由于產物會重新返回產物導致k的降低的效應,但點這很難考慮,本文不涉及)。總的來說,過渡態理論有很好的實用性,通常可以得到不錯的結果,但也有不太適用的情況,諸如高溫(會偏離IRC較大,產物返回反應物幾率高)、低壓(反應物間的碰撞頻率小而難以達到熱力學平衡態)、動態效應強(如反應中間體存在很短暫,來不及達到熱力學平衡態)等情況。
2 KiSThelP程序的功能和特點
大家提到計算反應速率常數的程序時,往往會先想到Truhlar他們的Polyrate。此程序歷史悠久,在過渡態理論計算方面是功能最強大的,VTST類方法全支持,可以考慮多維隧道效應校正。但是這個程序使用較為復雜,量化初學者難以入手。2014年出現了一個叫KiSThelP的程序,目的也是基于過渡態理論計算反應速率常數,此程序完全開源免費,Java編寫,可以在此下載http://kisthelp.univ-reims.fr/download.php,介紹它的原文為J.Comp.Chem.,35,82(2014)。KiSThelP的功能不及polyrate強大,只能做TST和CVT方式的VTST,隧道效應校正只能考慮一維的,但是有個最大的好處就是有簡單易用的圖形界面,能在Windows下用,而且支持Gaussian的輸出文件。如果你只是想簡單算一下反應速率常數,解決一些眼前的實際問題或者讓文章內容更充實,又不想在反應速率常數的計算上涉水太深,那么KiSThelP就夠用了,沒必要花太多精力去鉆polyrate。
KiSThelP有以下功能
(1)計算熱力學屬性。
(2)計算反應平衡常數。
(3)通過TST或VTST(此程序里VTST特指CVT)計算單分子或雙分子反應的反應速率常數。可以以Wigner或Eckart方式考慮隧道效應校正。
(4)通過RRKM方法計算單分子反應速率常數。此時不支持隧道效應校正。
以上數據和一些相關的量都會在圖形界面里清晰地顯示出來,而且可以很方便地繪制這些數據隨溫度和壓力的變化圖。而且可以隨時在圖形界面上調節諸如諧振頻率校正因子、體系質量、振動頻率等參數查看結果的變化,十分便利。如果不熟悉諧振頻率校正因子的話,建議看看《談談諧振頻率校正因子》(http://www.shanxitv.org/221)。
KiSThelP的輸入文件是.kinp私有格式,用文本編輯器打開就會看到里面記錄了振動頻率、對稱數、體系質量、轉動慣量、勢能、是否為線型結構、電子態簡并度這些描述體系特征的信息,格式不復雜,可以自己隨意編輯。KiSThelP也支持讀入Gaussian03/09(或NWChem、GAMESS)的freq任務的輸出文件。
KiSThelP是Java寫的,因此在Windows、Linux、Mac OSX上都可以用。對于Windows用戶,需要先手動安裝Java運行環境(Java Runtime Environment, JRE),網上一搜就能找到下載地址。裝完之后雙擊kisthelp2014.jar即可啟動。
下面將要介紹此程序的基本使用。由于計算反應平衡常數就是個ΔG=-RTlnK的關系式,自行手算就行了,所以不介紹怎么用此程序算平衡常數。RRKM涉及的門道較多,本文也不談了。下面只介紹怎么算熱力學屬性和通過TST/VTST算速率常數。
本文用的是Gaussian 09W B.01和2014-May版KiSThelP。如果大家對熱力學量、TST、CVT、隧道效應校正不熟悉,建議先看看KiSThelP原文中的一些初步介紹。下面的例子涉及到的文件,以及程序的原文都可以在這里下載:/usr/uploads/file/20150610/20150610211532_58686.rar。
3 用KiSThelP計算熱力學數據
重要提示:本文的這一節如今已經沒有實際意義了。2020年筆者正式發布的Shermo 2.0程序在計算熱力學數據方面遠比KiSThelP強大、靈活得多,有了Shermo之后就完全沒必要用KiSThelP來算了熱力學數據了。參看《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552)。
這一節介紹用KiSThelP計算熱力學數據。這里先用Gaussian在B3LYP/6-31G*下對CH3NH2做個freq任務,得到CH3NH2.out文件。
啟動KiSThelP后,先在左上角選Session-New(無論用此程序做什么任務,都是先選這個)。之后選Calculation-Atom,Molecule。接下來可以選一個.kinp文件或者Gaussian的freq任務輸出文件。這里就選剛得到的CH3NH2.out。程序會自動把此文件中的能量、頻率等信息提取并轉換成相同目錄下的ch3nh2.kinp文件,并利用這些信息計算出熱力學數據,如下所示。
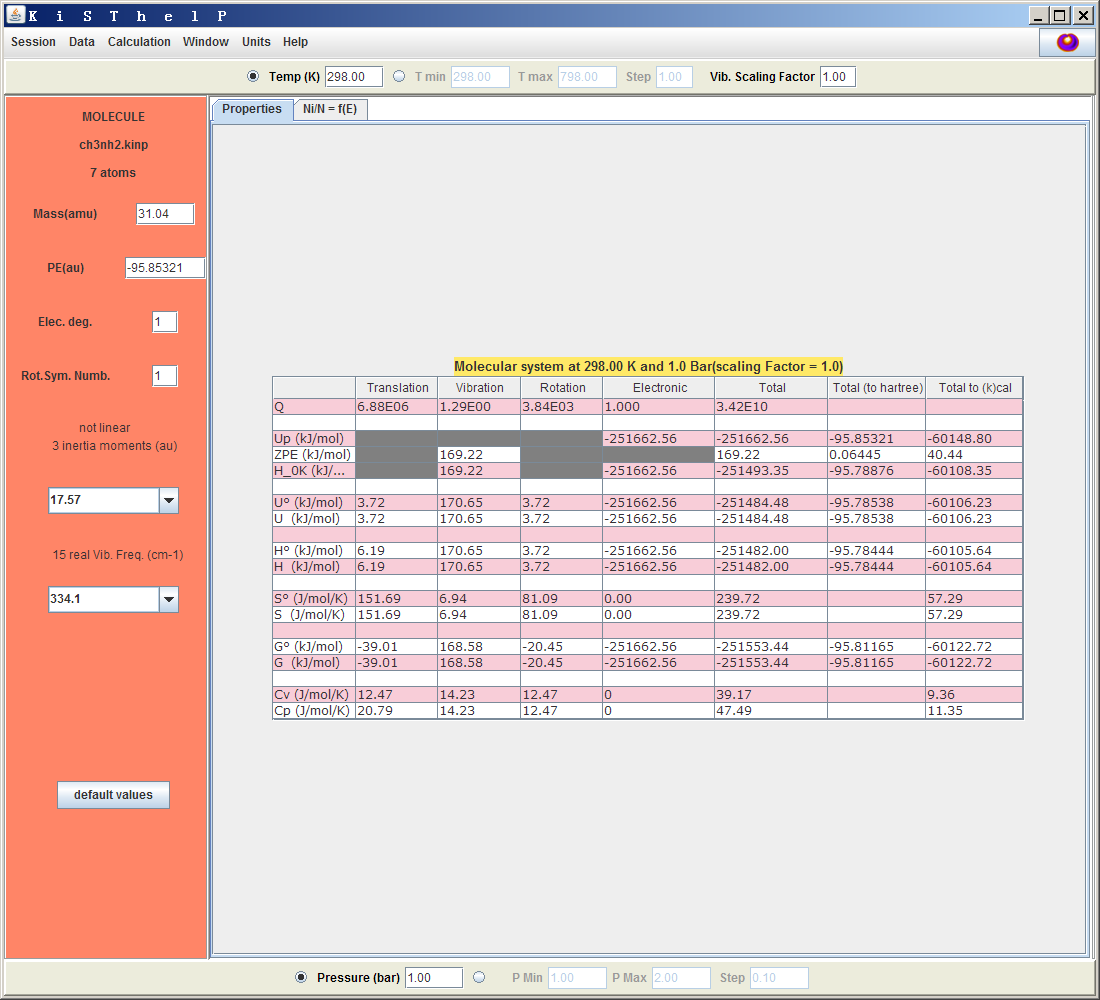
可見平動、振動、轉動和電子的配分函數Q,以及它們對體系的各種熱力學數據的貢獻都輸出出來了,每種數據的總值分別以kJ/mol、Hartree、kcal/mol來顯示。右上角帶個圓圈的量代表純氣體標準態(1bar)下的值。在界面中可以修改各個參數,比如上方的Vib.Scaling Factor(諧振頻率校正因子),改完之后按回車,表里的數據馬上就更新了。點Ni/N=f(E)標簽頁可以看到體系處于不同能量范圍的態的布居數曲線圖。
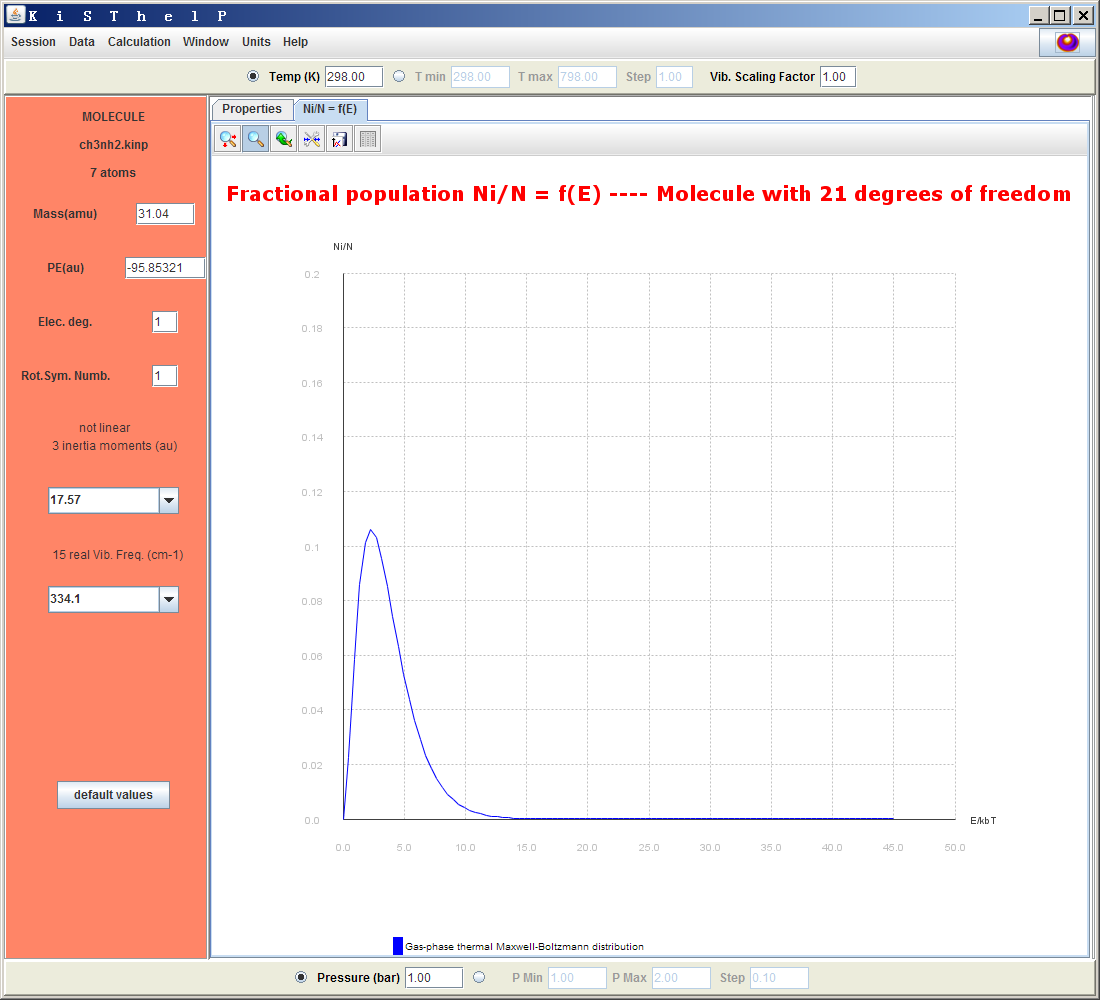
凡是這種圖,使用圖的左上角的按鈕都可以對圖進行縮放、調節坐標范圍、導出圖像、導出數據。
如果點擊界面上方的T min左邊的那個圓點,就可以對各種熱力學屬性隨溫度的變化來作圖。界面右側選擇熱力學屬性,T min和T max設定溫度范圍。例如下面是焓對溫度作圖
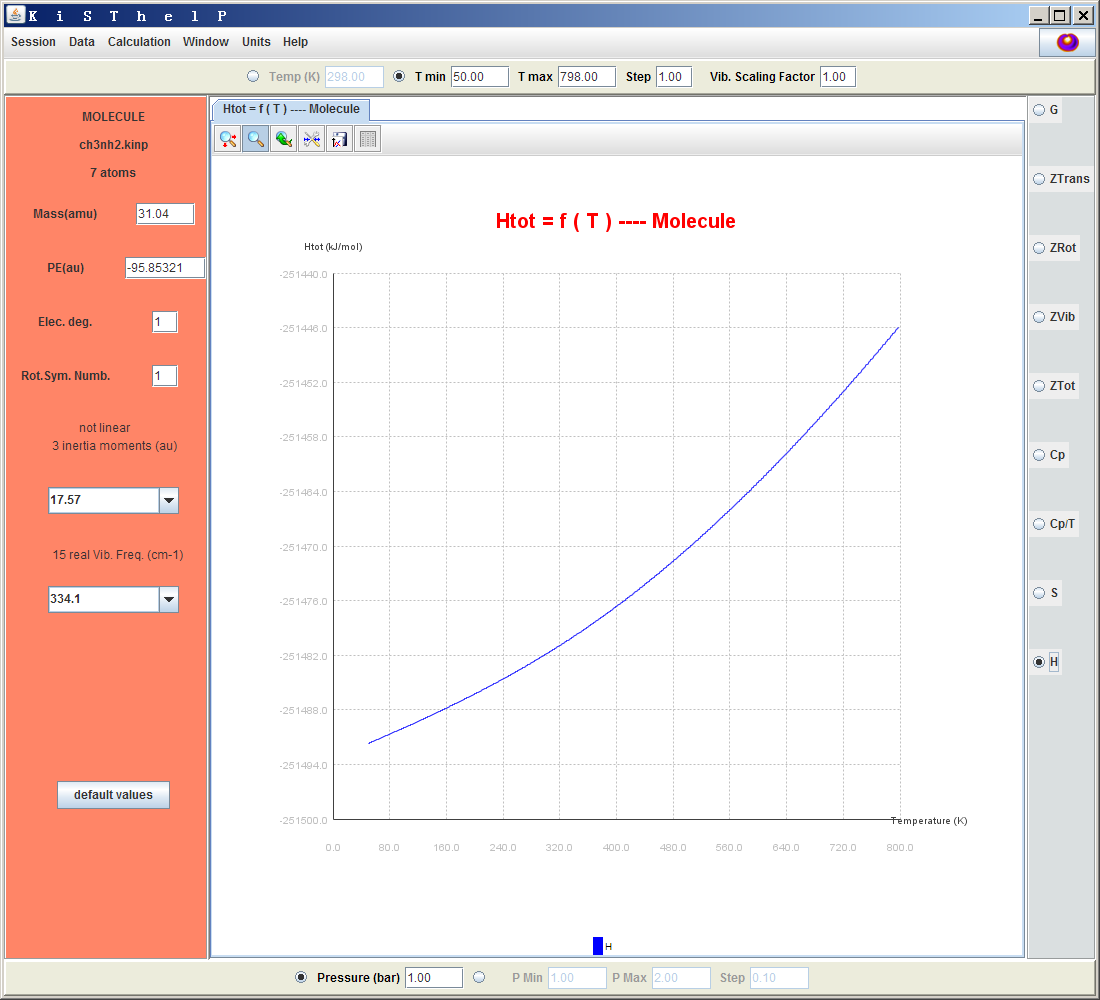
類似地,也可以令熱力學屬性對壓力的變化作圖。也就是選擇界面下方P Min左邊的圓點。
還可以令熱力學屬性同時對溫度和壓力的變化作圖,也就是既選中T min左邊的圓點也選擇P Min左邊的圓點,得到的就是二維曲面圖。
如果想再分析其它體系,應先選Calculation-Reset將程序的狀態重置。
KiSThelP計算熱力學數據和Gaussian的freq任務輸出的那些熱力學數據是完全一致的。用KiSThelP的主要優勢是可以方便、隨意地修改各種參數并馬上得到新的結果,還可以方便地令數據對溫度和壓力作圖來考察環境的影響。
4 用KiSThelP做過渡態理論計算
KiSThelP做過渡態計算需要兩類輸入文件
(1)反應物的輸入文件(.kinp文件或freq任務的.out文件)。如果是單分子反應,輸入文件就是那個反應物分子;如果是雙分子反應,就需要分別載入那兩個反應物分子。
(2)反應路徑.kinp文件。這種文件通過將IRC路徑上各個點的.kinp或freq任務的.out文件合并來得到,記錄了反應路徑上各個點的信息。如果是TST計算,只需要獲得過渡態的.kinp/.out文件,然后轉換成反應路徑的.kinp即可,也就是說此時的反應路徑只包含一個點的信息。如果是VTST,則需要把過渡態以及它鄰近的IRC路徑上的諸多點(點越多、越密結果越準確)的.kinp/.out文件合并成反應路徑的.kinp文件,因此計算量明顯大于TST,操作步驟也更多。
Wigner方式的隧道校正很簡單,基于過渡態的虛頻就能得到,也就是說不需要額外算什么,是“免費”的校正。而如果用Eckart方式考慮隧道效應校正,還會讓你手動輸入逆向勢壘,也就是說還得額外對產物做優化和振動分析。
下面就以氣相下甲烷的氫抽取反應CH4+H -> CH3-H-H (TS) -> CH3+H2為例來介紹具體怎么使用KiSThelP。計算級別為M062X/6-311G**。
4.1 TST計算實例
首先用以下輸入文件對反應物1進行優化和振動分析,得到CH4.out
#p M062x/6-311G** opt freq
Reactant 1
0 1
C -0.00000000 0.00000000 0.00000000
H -0.00000000 0.00000000 1.09000000
H -0.00000000 -1.02766186 -0.36333333
H -0.88998127 0.51383093 -0.36333333
H 0.88998127 0.51383093 -0.36333333
用以下輸入文件對反應物2進行熱力學計算,得到H.out
#P M062x/6-311G** freq
Reactant 2
0 2
H
用以下輸入文件搜索過渡態結構,并進行振動分析,得到TS.out
#P M062x/6-311G** opt(calcfc,ts) freq
TS
0 2
C -0.00000000 -0.00000000 -0.34155733
H 0.00000000 0.00000000 0.89844267
H 0.88112765 -0.50871929 -0.73043157
H -0.88112765 -0.50871929 -0.73043157
H -0.00000000 1.01743857 -0.73043157
H -0.00000000 0.00000000 1.86652082
啟動KiSThelP,選Session-New,再選Data-Build R Path.kinp來構建用于TST計算的反應路徑的.kinp文件。輸入1,選擇TS.out,然后在文件名的框里輸入TSTpath,這樣就得到了TSTpath.kinp。
選Calculation-k/TST/W-Bimolecular,依次選擇CH4.out、H.out、TSTpath.kinp(遇到提示框時直接選OK),然后就看到結果了。這個過程中CH4.out和H.out也會被自動轉換為ch4.kinp和h.kinp。
先不要馬上就討論結果。應該先確保窗口左側的反應路徑簡并度設對了,默認是1。反應路徑簡并度σ可以根據這個式子來算(詳見Theor Chem Account (2007) 118:813–826):
σ=σ(R)*n(TS)/ [σ(TS)*n(R)]
這里σ(R)和σ(TS)指的是反應物和過渡態結構的轉動對稱數,n(R)和n(TS)指的是反應物和過渡態結構的手性異構體數目。在Gaussian計算時,只要點群識別對了,在freq任務輸出文件中看到的Rotational symmetry number就是指的這個轉動對稱數,上面那篇TCA文章里的表2也給出了各種點群的轉動對稱數。對于當前的反應,甲烷是Td點群,轉動對稱數為12;過渡態是C3v點群,轉動對稱數是3,因此反應路徑簡并度為12/3=4。其物理意義也很容易理解,因為甲基的四個氫都可以被外來的氫原子所抽取。設完后,會看到表中的反應速率常數k成為了原先的4倍。
另外,最好也把諧振頻率校正因子考慮進去,這會略微改進熱力學屬性以及反應速率常數的計算結果。M06-2X/6-311G**沒有現成的校正因子,但是從http://comp.chem.umn.edu/freqscale/version3b1.htm上能找到M06-2X/6-31+G**的值(0.967),又由于對于其它理論方法6-31+G**和6-311G**的校正因子很接近,后者比前者略微大一點點,因此這里我們稍微估算一下,取0.97作為校正因子,輸入到窗口右上方的Vib. Scaling Factor里面。
現在,窗口里的數據如下所示
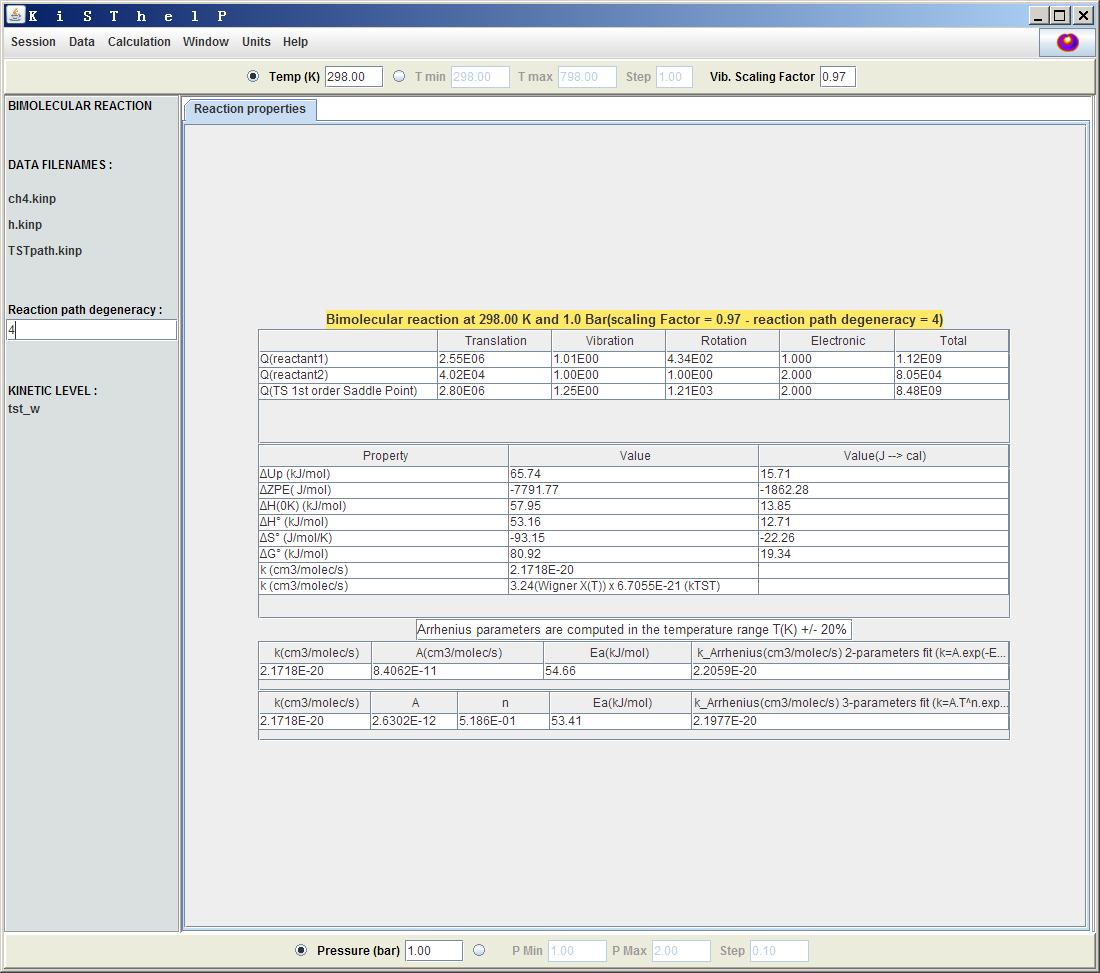
圖中靠上的表列出了反應物1和2以及過渡態的配分函數,中間的表顯示了過渡態的各種熱力學數據相對于反應物的熱力學數據的變化,并根據其中ΔG0(1bar標準態的活化自由能)通過過渡態理論得出反應速率常數(倒數第二行,2.17E-20)。最后一行顯示了倒數第二行的數值具體是怎么來的,由圖可見此例的Wigner隧道效應校正因子為3.24,即隧道效應使得反應速率常數增大到了原先的3.24倍。下方的表給出了根據阿倫尼烏斯公式擬合出的指前因子A和活化能Ea,以及基于擬合參數得到的反應速率常數k_Arrhenius,這個值和k符合得越好說明擬合得越準確,此例就擬合得較好。擬合所用的溫度范圍是當前設的溫度的±20%以內。注意阿倫尼烏斯公式k=A*exp(-Ea/RT)只是一個k隨T變化的經驗、宏觀層面上的公式,其中的A和Ea都只是根據理論或實驗得到的k隨T的變化而擬合得到的,不要和過渡態理論混淆,過渡態理論才是直接算出k的方法。基元反應的Ea和ΔG0雖關系密切,有相似的物理意義,但來源完全不同。而對于多步反應,每步都能算出一個ΔG0,但根據阿侖尼烏斯公式擬合出的則是一個整體的宏觀的Ea。最后一行是根據用得較少的三參數的阿倫尼烏斯公式k=A*T^n*exp(-Ea/RT)擬合出的參數。
值得一提的是,在計算表中的ΔU、ΔH、ΔG等過渡態相對于反應物的熱力學性質的變化的時候,反應物的熱力學量來自于反應物1和反應物2的熱力學量的直接加和,因此參考態取的是彼此間無限遠離的反應物1和反應物2,而非它們在反應前通過弱相互作用形成的復合物。另外,在做TST計算時,反應物和過渡態在計算轉動配分函數的時候轉動對稱數都被程序當成了1,因為轉動對稱數已經體現在了用戶輸入的反應路徑的簡并度里面。由于轉動對稱數直接影響轉動配分函數,因此對于轉動對稱數不為1的體系,做TST時顯示的它的轉動配分函數(以及基于它得到的熵和自由能)與單獨對它計算熱力學屬性時得到的值會存在差異。
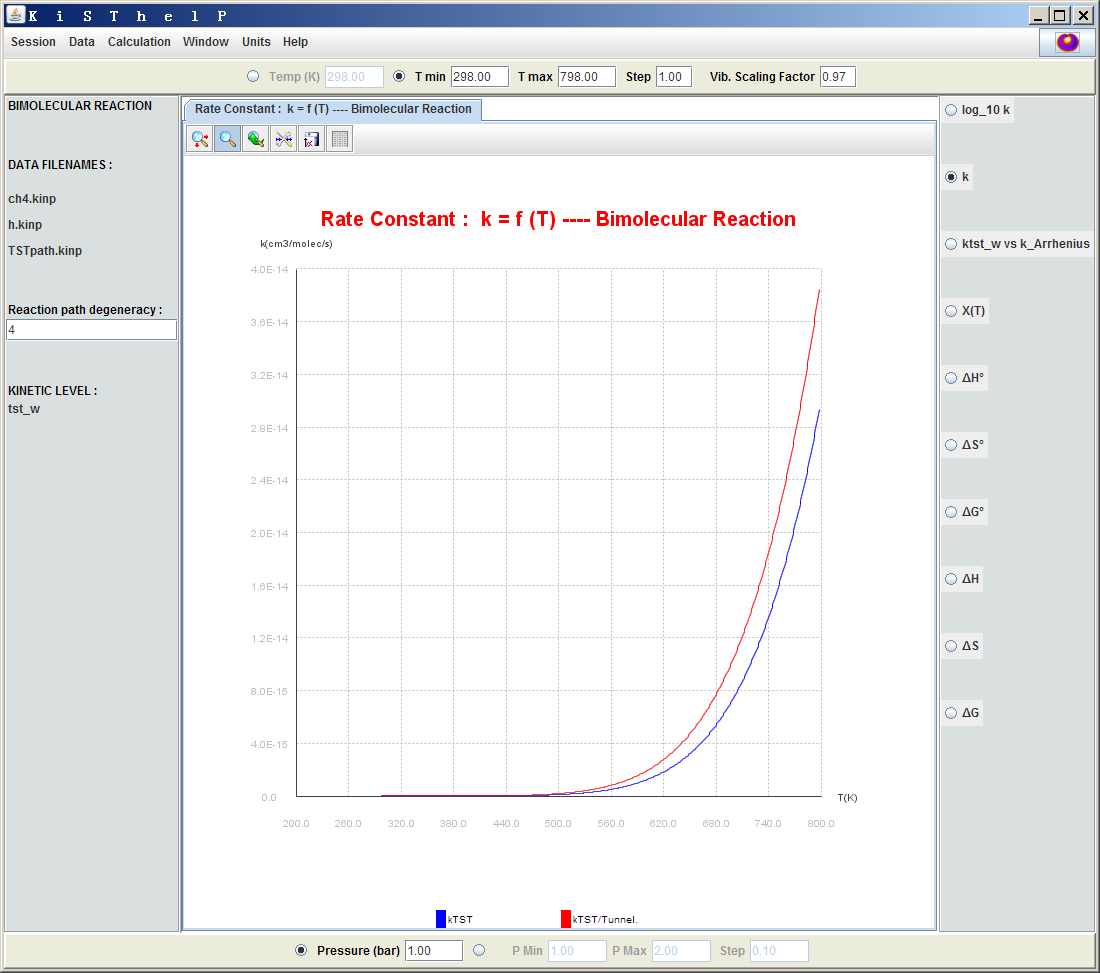
可以令k以及ΔG、ΔS、ΔH、透射系數等數值對溫度或者壓強來作圖,也就是點擊T min或P min左邊的按鈕,然后在窗口右邊選擇對應的量。下面是隧道效應校正前(藍線)和校正后(紅線)的k隨溫度的變化曲線。
如果TST計算中要以Eckart方式做隧道效應校正的話,選Session-New,把Vib. Scaling Factor設好,選Calculation-k/TST/Eck,之后操作步驟和上述一樣,只是程序最后會讓你輸入逆向反應的零點能校正后的勢壘,即逆向的ΔH(0K)。為了得到這個量,對于當前例子,就需要分別對產物CH3和H2進行優化和振動分析,然后用KiSThelP得到過渡態的H(0K)并減去CH3和H2的H(0K)。計算過程中諧振頻率校正因子應當和TST計算時用的一致。此例中CH3、H2和過渡態的H(0K)分別為-104471.17、-3041.43和-107458.94 kJ/mol,故逆向的ΔH(0K)為-107458.94-(-104471.17-3041.43)=53.66KJ/mol
反應物為單分子的情況,計算方法和上述一樣,區別僅在于在菜單中選Unimolecular而非Bimolecular。
4.2 VTST計算實例
這一節來做CVT方式的VTST計算。除了反應物、過渡態的freq任務的輸出文件外,VTST計算還需要IRC路徑上在過渡態附近的幾個點的freq任務的輸出。因此我們首先做IRC計算。
執行下面這個文件得到IRC,正方向和逆方向皆10個點。結構來自上一節優化出的過渡態的結構。
#p M062x/6-311G** IRC(calcfc,maxpoints=10)
IRC
0 2
C 0.00000000 0.00000000 0.26935900
H 0.00000000 0.00000000 -1.13595200
H 0.00000000 1.05670600 0.51542100
H -0.91513500 -0.52835300 0.51542100
H 0.91513500 -0.52835300 0.51542100
H 0.00000000 0.00000000 -2.02646400
然后把過渡態和距離它最近的正向4個和逆向4個點的坐標提取出來,寫成freq任務的輸入文件。具體來說,在gview里打開IRC任務的輸出文件,會看到21個幀,把第7~15幀分別保存成名為TS-4,TS-3,TS-2,TS-1,TS-0,TS+1,TS+2,TS+3,TS+4的.gjf文件,其中TS-0對應于過渡態結構,-和+代表逆向和正向。然后可以通過Ultraedit等程序批量修改關鍵詞使之成為freq任務。然后批量執行它們。
之所以VTST要做IRC并計算頻率,目的是得到IRC路徑上的自由能變化,從而找出IRC路徑上自由能的最大點位置,在這個點上按照TST公式得到的k就是VTST的k。而原始的TST是在過渡態結構上計算的,它相當于IRC上電子能量的最大點。由于IRC上自由能最大點和電子能量最大點的位置往往不會相差太遠,所以做VTST并不需要從反應物到產物完整的IRC路徑上各個點的信息,只要有過渡態附近的IRC上的點就足夠確定自由能最大點位置了。所以我們既不用把maxpoints設得很大以保證IRC能一直延伸到反應物和產物,也不需要對距離過渡態太遠的點做freq任務。但為了使得精度更高,在計算IRC的時候,可以把步長設得比默認小一點。步長默認是0.1amu^-0.5 bohr,可以通過IRC(stepsize=n)設為n*0.01amu^-0.5 bohr。步長設小的話,取的IRC點的數目就需要相應地增加。
啟動KiSThelP,選Session-New,Data-Build R Path.kinp,選擇TS-4.out,然后輸入此結構在反應路徑上的位置,輸入-0.4。然后選TS-3.out,輸入-0.3。以此類推,對于TS-0.out輸入0.0。最后選的是TS+4.out,輸入0.4。當9個文件都載入后,會讓你輸入要保存的反應路徑的.kinp文件名,輸入VTSTpath。
之后和上一節的操作完全一樣。主菜單選Calculation,然后根據需要選k/VTST、k/VTST/W、k/VTST/Eck當中的一種,并選擇單分子還是雙分子反應,然后選反應物的.kinp/.out文件,最后選反應路徑文件VTSTpath.kinp即可。
這里我們選k/VTST/W,輸出的信息和上一節的類似,只不過熱力學屬性中多了一列Value (TS at ΔG0 Max),這就是指的VTST的結果,即IRC路徑上ΔG最大點位置的結果。而Value (TS at first-order saddle point)那一列就是TST的結果,和上一節的結果完全一樣。
有趣的是,對于當前這個例子,VTST和TST的結果是相同的,也就是說,IRC路徑上電子能量最大點位置和自由能最大點位置是一樣的,這純屬巧合,在其它反應中或者其它計算級別中通常會有所不同。如果點擊Energy profile標簽頁,會看到反應路徑上ΔE(電子能量相對于反應物的變化)、ΔH0(0K)和ΔG0(T)的曲線圖,如下所示。
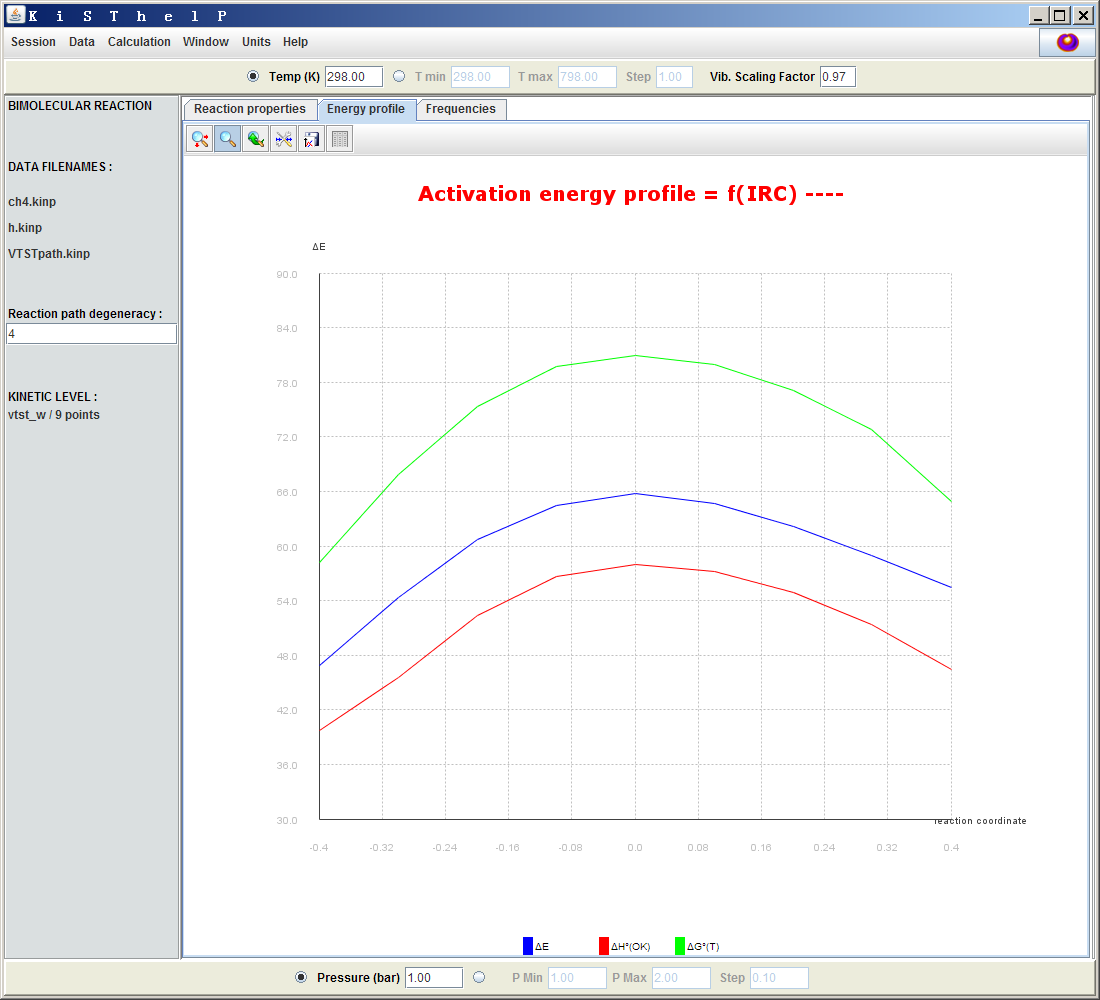
可見對于此例這三條曲線數值不同,但形狀相似,特別是最大點的位置是一樣的,都是反應坐標為0的位置。定位精度和構建反應路徑.kinp文件所用的點數有關,目前是9個點,相對粗糙,如果是比如用多達200個點,那么ΔG0(T)和ΔE的極大點位置的細微差異可能就能體現出來了,TST和VTST結果也將出現微小分歧了。(個人覺得KiSThelP應該在這個地方增加一個曲線擬合功能)
點擊Frequencies標簽頁的話,將會看到體系每個振動頻率隨反應坐標的變化,如下所示。
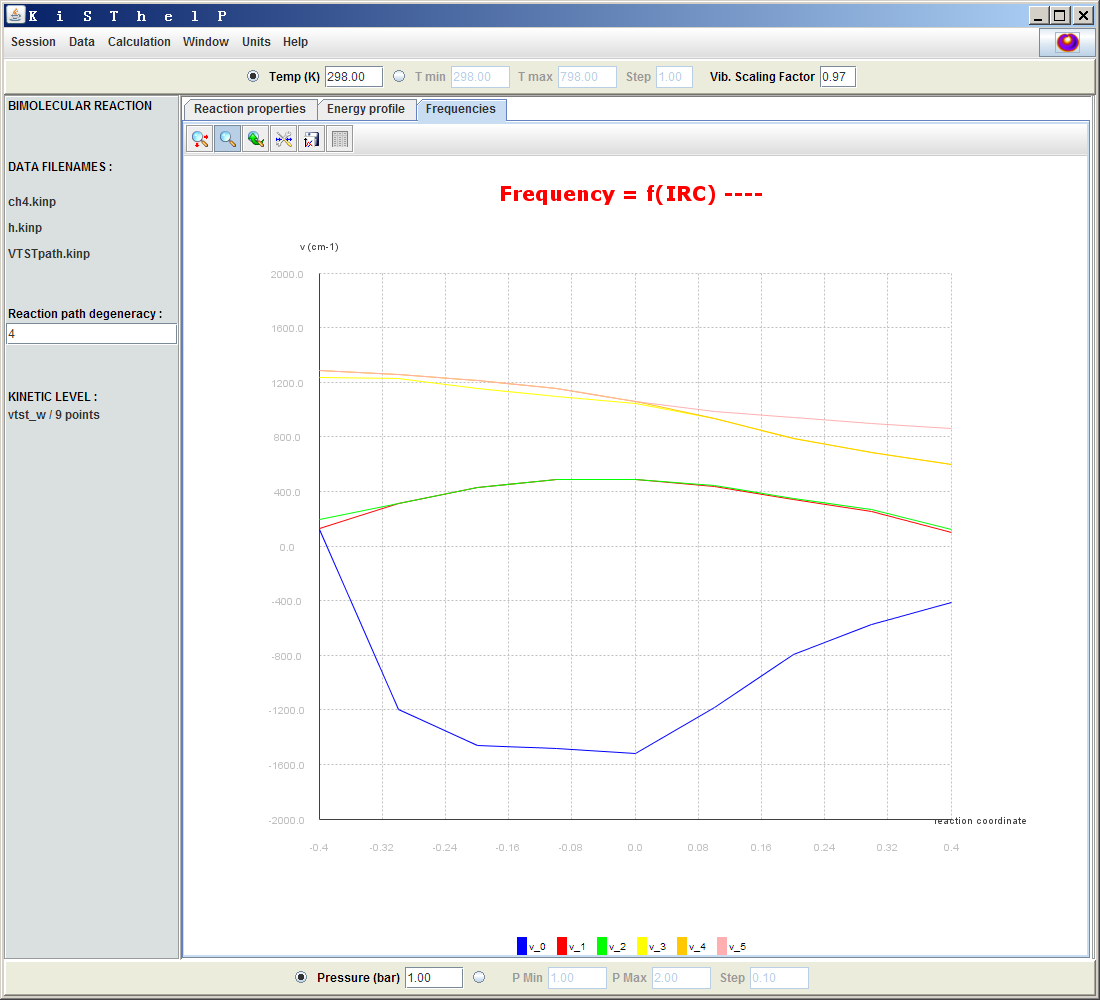
在過渡態位置,即0.0處,可見只有一個虛頻,也就是藍色曲線。這個虛頻在過渡態位置處數值最負(以負值代表虛數)。在IRC上與過渡態相距越遠,這個虛頻就變得越正,逐漸接近于0。當遠到一定程度,比如-0.4那個點的位置,這個振動模式就不再是虛頻了。其它各個振動模式的頻率也在圖中十分清楚直觀地展現了出來,分析起來很便利。
5 總結&其它
雖然過渡態理論,特別是其原始版本,形式不復雜,自己去編程計算也不很困難,但是,就是這么簡單的事情,卻長期也沒有個簡單、易用的程序去計算,使量化初學者或外行人研究反應速率問題遇到很大的阻礙。KiSThelP可謂是很好地彌補了這一空白。雖然這程序不算很強大,但最基本、最重要的功能都有了,滿足一般需求也夠了,操作很便捷,結果清晰易懂,還能方便地繪圖,不僅很實用,當成教學用的程序也非常適合。
這個程序的源代碼包里有一些示例文件,感興趣的話可以看看。程序的網站上還有教學視頻,但是不夠詳細,很多地方根本沒說清楚,而且錄制時用的版本和當前版本在某些界面上也略有差異,感興趣的話也可以看看。
前面舉的例子是氣相下的,對于溶液下反應。可以在隱式溶劑模型下做前述計算。
量化計算中,幾何優化時選用的級別通常比計算單點時更低,從而在保證精度的前提下降低耗時,可參考《淺談為什么優化和振動分析不需要用大基組》(http://www.shanxitv.org/387)。在KiSThelP中計算k時如果也想這么做的話,應當先把Gaussian等程序的輸出文件按前文所述的方式轉換成kinp文件,然后把kinp里的勢能部分的能量手動改為高級別單點能數據,然后在計算k的時候用kinp作為輸入文件。
默認情況下,KiSThelP對每種振動模式都是以諧振子模型或結合諧振頻率校正因子的方式來考慮。但是如果振動模式對應于大幅度內部轉動,諧振子模型就不合適了,此時在KiSThelP里可以以受阻轉子方式來考慮。這需要計算出勢壘高度,然后寫進.kinp里的相應的振動頻率的后面,具體參見程序自帶文檔的介紹,示例文件里面也有相關的。
有的時候,反應物以不同構象參與反應,得到不同產物。例如B以不同構象B_1和B_2參與反應時分別得到C_1和C_2,可寫為這樣:
[A][B]k1->[C1]
[A][B]k2->[C2]
如果要求k1和k2,應當這么處理:
根據玻爾茲曼公式,可算出B_1和B_2在B中的比例w,即
[B_1]=[B]*w1
[B_2]=[B]*w2
上式可寫為
[A][B_1]k1'->[C1]
[A][B_2]k2'->[C2]
其中k1=k1'*w1,k2=k2'*w2
把A+B_1和A+B_2分別作為反應物,按本文過程由KiSThelP得到k1'和k2'。然后根據玻爾茲曼公式算出權重w1和w2,乘上去,就得到了不同方式反應的反應速率常數k1和k2。如果不熟悉玻爾茲曼權重的計算,可參見《根據Boltzmann分布計算分子不同構象所占比例》(http://www.shanxitv.org/165)。