使用Multiwfn計算原子的C6色散系數
使用Multiwfn計算原子的C6色散系數
Using Multiwfn to calculate atomic C6 dispersion coefficients
文/Sobereva@北京科音 2024-May-18
1 前言
絕大多數分子力場表現色散吸引部分都是基于原子的C6色散系數進行計算的,原子間色散作用能表達為-C6/r^6,其中r為原子間距離。著名的DFT-D3色散校正(http://www.shanxitv.org/210),以及Tkatchenko-Scheffler (TS)等色散校正方法,也都是依賴于原子的C6色散系數計算校正能。顯然,C6色散系數是一個很重要的量。本文介紹怎么用Multiwfn程序(http://www.shanxitv.org/multiwfn)通過TS方法計算原子的C6色散系數。看完了本文,讀者也同時會知道如何算分子間的C6系數。使用本文的方法計算發表文章時,記得需要按照Multiwfn啟動時屏幕上的提示對程序進行恰當引用。
2 背景知識
原子在孤立狀態的C6系數已經有很多文章報道,例如JCP, 121, 4083 (2004)給出了前五周期除Zr-Cd外各個元素的C6。JCTC, 12, 3603 (2016)還給出了整個周期表各種元素及部分元素離子態的C6。原子的C6系數是嚴重受到化學環境的影響的,計算實際化學體系中的原子C6系數沒有唯一方法,不同研究者提出了不同策略,有的粗糙有的精確,有的簡單有的復雜。例如DFT-D3色散校正基于原子的配位數進行計算,DFT-D4(http://www.shanxitv.org/464)還額外依賴于原子電荷,XDM色散校正基于實際電子密度計算。一種實現起來簡單的方法是PRL, 102, 073005 (2009)中提出的TS色散校正方法用的策略,它將分子中某原子A的C6系數表達為
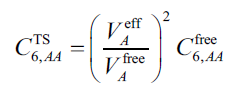
其中V_eff和V_free分別是原子在當前分子中的有效體積以及它在孤立狀態下的體積(自由體積)。注意這兩個體積和一般意義的體積并不是一回事,務必看《使用Multiwfn計算分子中的原子極化率》(http://www.shanxitv.org/600)了解其定義和細節。上式中C6_free是原子在孤立狀態下的C6系數,如前所述這在文獻里已經給了。一旦有了各個原子的C6系數,就可以計算不同原子間的C6系數,如下所示,其中α_eff(0)是原子在分子中的靜態極化率,計算方式在《使用Multiwfn計算分子中的原子極化率》中專門說了。
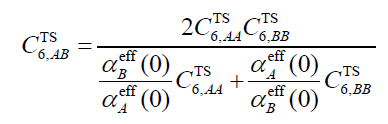
利用原子間的C6系數,還可以進一步計算分子間的C6系數,如下所示,A和B分別循環兩個分子的各個原子。
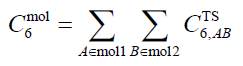
分子間的C6系數也可以通過dipole oscillator strength distributions (DOSD)實驗數據得到,例如在JCP, 123, 024101 (2005)中給出了178個分子間和少量分子-原子間C6系數。值得一提的是,有了分子間C6系數也可以擬合出不同原子類型間的C6系數,例如JCP, 116, 515 (2002)。
計算原子在分子中的有效體積V_eff的時候涉及到將分子空間劃分成原子空間,這由原子權重函數體現,這有很多定義,例如AIM、Becke、Hirshfeld、Hirshfeld-I、MBIS、Voronoi等。在MBIS原文JCTC, 12, 3894 (2016)當中第5節做了對比測試,TS方法與MBIS相結合表現得最好,得到的分子C6系數與實驗值相差最小,方均根百分比誤差為6.9 %。文中測試時是基于B3LYP/6-311+G(2df,p)級別得到的波函數算的密度。
3 計算方法
Multiwfn從2024-May-17更新的版本開始支持了計算原子C6色散系數,此版本的原子空間劃分支持Becke、Hirshfeld、Hirshfeld-I和MBIS。如果你不了解Multiwfn的話,務必看《Multiwfn FAQ》(http://www.shanxitv.org/452)和《Multiwfn入門tips》(http://www.shanxitv.org/167)。Multiwfn可以在其官網http://www.shanxitv.org/multiwfn免費下載。
Multiwfn計算C6系數的操作和要求的輸入文件和《使用Multiwfn計算分子中的原子極化率》(http://www.shanxitv.org/600)介紹的嚴格一致,Multiwfn在輸出原子極化率之后就會輸出原子C6系數。在輸入文件方面,簡單來說,需要提供當前體系的波函數文件,格式可以是mwfn/wfn/fch/molden等等,產生方法見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。而且還需要提供當前體系中每種元素的波函數文件,用量子化學程序對相應元素原子做單點計算即可得到,注意自旋多重度應當對應基態的。下面就給出一個具體計算例子。
4 實例
此例對CCl4進行計算。計算級別使用前面提到的JCTC, 12, 3894 (2016)測試時所使用的B3LYP/6-311+G(2df,p),CCl4的幾何優化也在這個級別。注意這個級別未必就是最佳選擇,畢竟文中作者也沒做過對比測試。此例用到的CCl4分子、C和Cl原子的fch格式的波函數文件在http://www.shanxitv.org/attach/709/file.zip里都提供了,其中用于產生它們的Gaussian的輸入輸出文件也都給了。
啟動Multiwfn,然后輸入
CCl4.fch //分子波函數文件的實際路徑
15 //模糊空間分析
-1 //修改原子空間定義方式
5 //MBIS方法
1 //開始產生MBIS原子空間。這是個迭代過程
13 //計算原子有效體積、自由體積、極化率和C6系數
C.fch //C原子的波函數文件的實際路徑
Cl.fch //Cl原子的波函數文件的實際路徑
馬上就算完了,結果如下
...略(原子有效體積、自由體積、極化率信息)
Atomic C6 coefficients estimated using Tkatchenko-Scheffler method:
1(C ): 41.22 a.u. (Ref. data: 46.6 a.u.)
2(Cl): 95.94 a.u. (Ref. data: 94.6 a.u.)
3(Cl): 95.94 a.u. (Ref. data: 94.6 a.u.)
4(Cl): 95.94 a.u. (Ref. data: 94.6 a.u.)
5(Cl): 95.94 a.u. (Ref. data: 94.6 a.u.)
Note: Reference data denotes the built-in value of free-state atom
Homomolecular C6 coefficient: 2076.98 a.u.
可見C和Cl的C6系數分別為41.22和95.94 a.u.。Ref. data對應的是相應元素在孤立狀態下的C6值,取自JCP, 121, 4083 (2004)。如果這里顯示的是0,說明此文里沒給此元素的孤立狀態C6值,只能自己從其它地方獲取,并根據前面輸出的原子有效體積和自由體積按照第2節介紹的公式手動計算此原子在分子中的C6。
由上還可以看到homomolecular的C6系數,這是指Multiwfn根據自動算的原子間的C6系數得到的CCl4與CCl4分子間的C6系數。當前值2076.98 a.u.非常接近JCP, 123, 024101 (2005)給出的實驗值2024 a.u.,計算得很成功!注意不是對所有體系都能和實驗吻合得這么好,當前屬于表現較好的情況。
也可以考察一下改成Hirshfeld原子空間時的結果如何。運行以下命令
-1 //修改原子空間定義方式
3 //Hirshfeld方法,且基于Multiwfn內置的球對稱化的原子電子密度進行計算
13 //計算原子有效體積、自由體積、極化率和C6系數
此時的結果為
Atomic C6 coefficients estimated using Tkatchenko-Scheffler method:
1(C ): 40.84 a.u. (Ref. data: 46.6 a.u.)
2(Cl): 89.02 a.u. (Ref. data: 94.6 a.u.)
3(Cl): 89.02 a.u. (Ref. data: 94.6 a.u.)
4(Cl): 89.02 a.u. (Ref. data: 94.6 a.u.)
5(Cl): 89.02 a.u. (Ref. data: 94.6 a.u.)
Note: Reference data denotes the built-in value of free-state atom
Homomolecular C6 coefficient: 1945.22 a.u.
可見當前homomolecular的C6系數1945.22 a.u.與實驗值的誤差明顯大于用MBIS原子空間時的。根據JCTC, 12, 3894 (2016)的測試,從統計結果來看,MBIS比Hirshfeld的整體誤差更小,但對于特定分子,也往往出現Hirshfeld的誤差更小的情況。