過渡態、反應路徑的計算方法及相關問題
前言:本文主要介紹過渡態、反應路徑的計算方法,并討論相關問題。由于這類算法極多,可以互相組合,限于精力不可能面面俱到展開,所以只介紹常用,或者實用價值有限但有啟發性的方法。文中圖片來自相關文獻,做了一定修改。由于本文作為帖子發布,文中無法插入復雜公式,故文中盡量將公式轉化為文字描述并加以解釋,這樣必然不如公式形式嚴謹,而且過于復雜的公式只能略過,但我想這樣做的好處是更易把握方法的梗概,有興趣可以進一步閱讀原文了解細節。雖然絕大多數人不專門研究計算方法,其中很多方法也不會用到,但多了解一下對開闊思路是很有好處的。筆者后來還寫了《簡談Gaussian里找過渡態的關鍵詞opt=TS和QST2、3》(http://www.shanxitv.org/460)一文,專門針對Gaussian里找過渡態的關鍵詞的具體使用問題進行了說明,建議Gaussian用戶都看看。
文中指的“反應”包括構象變化、異構化等任何涉及到過渡態的變化過程。“反應物”與“產物”泛指這些過程的初態和末態。“優化”若未注明,包括優化至極小點和優化至過渡態。勢能面是高維的,但為了直觀以及表述方便,文中一般用二維勢能面模型來討論,應推廣至高維情況。限于純文本格式,向量、矩陣無法加粗表示,但容易自行判斷。
如果想了解更多的關于優化、找過渡態、產生IRC算法的細節以及數學方面的東西,參看“幾何優化、過渡態搜索、IRC綜述與原文合集”(http://bbs.keinsci.com/thread-105-1-1.html)。
目錄:
1.過渡態2.過渡態搜索算法
2.1 基于初猜結構的算法
2.1.1 牛頓-拉弗森法(Newton-Raphson,NR)與準牛頓法(quasi-Newton,QN)
2.1.2 AH方法(augmented Hessian)
2.1.2.1 RFO法(Rational Function Optimization,有理函數優化)
2.1.2.2 P-RFO法(Partitioned-RFO)
2.1.2.3 QA法(Quadratic Approximation,二次逼近)
2.1.2.4 TRIM法(trust-region image minimization,置信區域鏡像最小化)
2.1.2.5 在高斯中的常見問題
2.1.3 GDIIS法(Geometry Direct Inversion in the Iterative Subspace)
2.1.4 梯度模優化(gradient norm minimization)
2.1.5 Dimer方法
2.2 基于反應物與產物結構的算法
2.2.1 同步轉變方法(synchronous transit,ST)
2.2.2 STQN方法(Combined Synchronous Transit and Quasi-Newton Methods)
2.2.3 贗坐標法(pseudo reaction coordinate)
2.2.4 DHS方法(Dewar-Healy-Stewart,亦稱Saddle方法)與LTP方法(Line-Then-Plane)
2.2.5 Ridge方法
2.2.6 Step-and-Slide方法
2.2.7 Müller-Brown方法
2.2.8 CI-NEB、ANEBA方法
2.3 基于反應物結構的算法
2.3.1 最緩上升法(least steep ascent,shallowest ascent)
2.3.2 本征向量/本征值跟蹤法(eigenvector/eigenvalue following,EF。也稱mode walking/mode following/Walking up valleys)
2.3.3 ARTn(activation-relaxation technique nouveau)
2.3.4 梯度極值法(Gradient extremal,GE)
2.3.5 約化梯度跟蹤(reduced gradient following,RGF)
2.3.6 等勢面搜索法(Isopotenial Searching)
2.3.7 球形優化(Sphere optimization)
2.4 全勢能面掃描
3.過渡態相關問題
3.1 無過渡態的反應途徑(barrierless reaction pathways)
3.2 Hammond-Leffler假設
3.2 對稱性問題
3.3 溶劑效應
3.4 計算過渡態的建議流程
4.內稟反應坐標(intrinsic reaction coordinate,IRC)
5.IRC算法
5.1 最陡下降法(Steepest descent)
5.2 IMK方法(Ishida-Morokuma-Kormornicki)
5.3 Müller-Brown方法
5.4 GS(Gonzalez-Schlegel)方法
6.chain-of-states方法
6.1 Drag method方法
6.2 PEB方法(plain elastic band)
6.3 Elber-Karplus方法
6.4 SPW方法(Self-Penalty Walk)
6.5 LUP方法(Locally Updated planes)
6.6 NEB方法(Nudged Elastic Band)
6.7 DNEB方法(Double Nudged Elastic Band)
6.8 String方法
6.9 Simplified String方法
6.10 尋找過渡態的chain-of-state方法
6.10.1 CI-NEB方法
6.10.2 ANEBA方法(adaptive nudged elastic band approach)
6.11 chain-of-states方法的一些特點
6.12 高斯中opt關鍵字的path=M方法
6.13 CPK方法(Conjugate Peak Refinement)
1.過渡態
本質上,電子、原子核的運動是相關而不可分割的,求解薛定諤方程得到的是描述二者狀態的總波函數和體系的總能量。在量子化學中,為簡化問題,一般采用BO(Born-Oppenheimer)近似。由于電子比原子核輕得多,其運動速度遠快于原子核,核坐標改變過程中的每一時刻電子的狀態可以立即調整以使能量最低,而以電子的視角看原子核就是不動的勢場,所以有理由將原子核運動與電子的運動分離開來。可以在每一組確定的核坐標情況下求解電子的薛定諤方程,電子能量加上核間互斥能即得到此幾何結構下的分子總能量。這種BO近似的做法由于在求解電子薛定諤方程時忽略了核運動,所以也稱為核不動近似。在BO近似下分子的能量是核坐標的函數,系統地變化核坐標,隨之變化的能量就構成了勢能面(potential energy surface,PES)。過渡態結構指的是勢能面上反應路徑上的能量最高點,它通過最小能量路徑(minimum energy path,MEP)連接著反應物和產物的結構(如果是多步反應的機理,則這里所指反應物或產物包括中間體)。對于多分子之間的反應,更確切來講過渡態結構連接的是它們由無窮遠接近后因為范德華力和靜電力形成的復合物結構,以及反應完畢但尚未無限遠離時的復合物結構。確定過渡態有助于了解反應機理,以及通過勢壘高度計算反應速率。一般來講,勢壘小于21kcal/mol就可以在室溫下發生。
在勢能面上,過渡態結構的能量對坐標的一階導數為0,只有在反應坐標方向上曲率(對坐標二階導數)為負,而其它方向上皆為正,是能量面上的一階鞍點。過渡態結構的能量二階導數矩陣(Hessian矩陣)的本征值僅有一個負值,這個負值也就是過渡態擁有唯一虛頻的來源。若將分子振動簡化成諧振子模型,這個負值便是頻率公式中的力常數,開根號后即得虛數。
分子構象轉變、化學反應過程中往往都有過渡態的存在,即這個過程在勢能面上的運動往往都會經歷滿足上述條件的一點。化學反應的過渡態更確切應當成為“反應過渡態”。需要注意的是化學反應未必都經歷過渡態結構。
由于過渡態結構存在時間極短,所以很難通過實驗方法獲得,直到飛秒脈沖激光光譜的出現才使檢驗反應機理為可能。計算化學方法在目前是預測過渡態的最有力武器,盡管計算上仍有一些困難,比如其附近勢能面相對于平衡結構更為平坦得多、低水平方法難以準確描述、難以預測過渡態結構、缺乏絕對可靠的方法(如優化到能量極小點可用的最陡下降法)等。
搜索過渡態的算法一般結合從頭算、DFT方法,在半經驗、或者小基組條件下,難以像描述平衡結構一樣正確描述過渡態結構,使得計算尺度受到了限制。結合分子力場可以描述構象變化的過渡態,但不適用描述反應過渡態,因為大部分分子力場的勢函數不允許分子拓撲結構的改變,雖然也有一些力場如ReaxFF可以支持,有的力場還有對應的過渡態原子類型,但目前來看適用面仍然較窄,而且不夠精確,盡管更為快速。
注:嚴格來說,“過渡結構”是指勢能面上反應路徑上的能量最高點,而“過渡態”是指自由能面上反應路徑上的能量最高點,由于自由能變主要貢獻自勢能部分,所以多數情況二者結構近似一致。為了計算上的簡單,常以勢能面近似表達自由能面,以下述方法得到的勢能面上反應路徑上的能量最高點做為過渡態。但隨著溫度升高,往往熵變的貢獻導致自由能面與勢能面形狀發生明顯偏離,從而導致過渡結構與過渡態明顯偏離,兩個詞就不能混用了,此時下述方法應該用在自由能面上找真正的過渡態。但本文不涉及相關問題,故文中過渡態、過渡結構一律指勢能面上反應路徑上的能量最高點。
2.過渡態搜索算法
2.1 基于初猜結構的算法
2.1.1 牛頓-拉弗森法(Newton-Raphson,NR)與準牛頓法(quasi-Newton,QN)
NR法是尋找函數一階導數為0(駐點)位置的方法。通過對能量函數的泰勒級數的二階近似展開,然后使用穩態條件dE/dr=0,可導出步進公式:下一步的坐標向量 = 當前坐標向量 - 能量一階導數向量 * Hessian矩陣的逆矩陣。在勢能面上以NR法最終找到的結果是與初猜位置Hessian矩陣本征值正負號一致、離初猜結構最近的駐點,由于能量極小點、過渡態和高階鞍點的能量一階導數皆為0,故都可以用NR法尋找。對于純二次形函數NR法僅需一步即可找到正確位置,而勢能面遠比之復雜,所以需要反復走步直至收斂。也因為勢能面這個特點,為了改進優化,實際應用中NR法一般還結合線搜索步(line search),對于優化至極小點,就是找當前點與NR法算出來的下一點的連線上的能量極小點作為實際下一步結構;若優化至過渡態,且連線方向主要指向過渡態,則找的是連線上能量極大點,若主要指向其它方向則找連線的能量極小點,若指向二者程度均等則一般不做線搜索。由于精確的線搜索很花時間,所以一般只是在連線的當前位置附近計算幾個點的能量,以高階多項式擬和后取其最小/最大點。
NR法每一步需要計算Hessian矩陣并且求其逆,所以十分昂貴。QN法與NR法的走步原理一樣,但Hessian矩陣最初是用低級或經驗方法猜出來的,每一步優化中通過當前及前一步的梯度和坐標對Hessian矩陣逆矩陣逐漸修正。由于只需計算一階導數,即便Hessian矩陣不準確造成所需收斂步數增加,但一般仍比NR法速度快得多。QN法泛指基于此原理的一類方法,常用的是BFGS(Broyden Fletcher Goldfarb Shanno),此法對Hessian的修正保持其對稱性和正定性,最適合幾何優化,但顯然不能用于找過渡態。還有DFP(Davidon-Fletcher-Powell),MS(Murtagh-Sargent,亦稱symmetric rank 1,SR1),PSB(Powell-symmetric-Broyden)。也有混合方法,如Bofill法是PSB和MS法對Hessian修正量的權重線性組合,比二者獨立使用時更好,權重系數通過位移、梯度改變量和當前Hessian計算得到,它對Hessian的修正不強制正定,很適宜搜索過渡態。
將NR步進公式放到Hessian本征向量為坐標的空間下其意義更為明顯(此時Hessian為對角矩陣),可看出在每個方向上的位移就是這個方向勢能的負梯度除以對應的本征值,比如在i方向上的位移可寫為ΔX(i)=-g(i)/h(i),在受力越大、曲率越小的方向位移越大。每一步實際位移就是這些方向上位移的矢量和。對于尋找過渡態,因為虛頻方向對應Hessian本征值為負,使位移為受力相反方向,所以NR法在過渡態附近每一步都是使虛頻方向能量升高,而在其它正交的方向朝著能量降低的方向位移,通過這個原理步進到過渡態。若有n個虛頻,則NR法就在n個方向升高能量而其它方向降低能量找到n階鞍點。
由于NR法的這個特點,為找到正確類型的駐點,初猜結構必須在目標結構的二次區域(quadratic region)內。所謂的二次區域,是指駐點附近保持Hessian矩陣本征值符號不變的區域,它的形狀可以用多變量的二次函數準確描述,例如二維勢能面情況下這樣的區域可以用F(x,y)=A*x^2+B*y^2+C*x+D*y+E*x*y來近似描述。對于能量極小點,就是指初猜點在目標結構附近Hessian矩陣為正定矩陣的范圍;對于找過渡態,就需要初猜點在它附近含有且僅含有一個負本征值的范圍內。并且這個范圍內不能有其它同類駐點比目標結構距離初猜結構更近。NR法方便之處是只需要提供一個初猜結構即可,但是由于過渡態二次區域很小(相對于能量極小點來講),復雜反應過渡態又不容易估計,故對使用者的直覺和經驗有一定要求,即便是老手,也往往需要反復嘗試。
NR法對初猜結構比較敏感,離過渡態越近所需收斂步數越少,成功機率越高。模版法可以幫助給出合理的初猜,也就是如果已經知道其它機理相同的反應的過渡態結構,可以保持反應位點部分的結構不變而替換周圍的原子,使之變成自己要研究的化合物反應的初猜結構。
2.1.2 AH方法(Augmented Hessian)
AH方法并不是獨立的尋找過渡態的方法,而是通過修改原始Hessian矩陣來調整NR法步進的長度和方向的一種方法。在NR法的步進公式中加入了一個移位參數λ,式子變為ΔX(i,λ)=-g(i)/(h(i)-λ),NR法相當于λ等于0時的特例。λ控制著每步步進距離,它與h(i)的相對大小也控制著這個坐標上的步進方向。根據設定λ方法的不同,常見的有RFO、P-RFO和QA/TRIM。這些方法每一步也使用QN方法來快速地更新Hessian。下面提及的置信半徑R(Trust radius)是指二階泰勒級數展開這種近似的合理的區域,可以在優化過程中固定也可以動態改變,比如下一步位置的實際能量與使用二階泰勒級數展開預測的能量符合較好則加大R,反之減小。優化的每一步移動距離不應超過R,否則可能進入二階泰勒級數展開近似的失效區域,NR法在勢能面平坦的時候容易超過這個范圍,應調整λ避免。
2.1.2.1 RFO法(Rational Function Optimization,有理函數優化)
與NR法不同的是,RFO對能量函數使用的是有理逼近展開,從形式上講就是將NR法的二階泰勒級數展開式作為分子,多添加了個分母項,可推得它與AH方法有形式相同的步進公式。確定其中λ的公式是λ=∑( g(i)^2/(h(i)-λ) ),g(i)和h(i)代表此方向的梯度和本征值,加和是對所有本征向量方向加和。通過迭代方法會解出N+1個λ(N代表勢能面維數),將λ按大小排列,則有λ(i)≤h(i)≤λ(i+1)。故選其中最小的λ可使各個方向位移公式的(h(i)-λ)項皆為正,保證每步位移都向著極小點。選其中大于m個Hessian本征值的λ,將會在本征值最低的m個方向上沿其上的受力反方向位移提升能量,在其余N-m個方向上降低能量,由此確保優化到m階鞍點,若m為1即用來找過渡態。所以用了這個方法尋找指定類型駐點不再像NR法對初猜位置Hessian本征值符號有要求,而是直接通過選擇λ來設定向著何種鞍點位移。如果每步步長度超過了R,則乘以一個小于1的因子來減小步長。值得一提的是,λ與勢能面維數N的平方根近似成正比,隨著體系尺度的增大,RFO的λ對NR法的二次近似就會趨現“校正過度”情況,產生大小不一致問題,可使用SIRFO(Size independent RFO)方法解決,即AH走步公式中的λ改為λ/N^0.5。2.1.2.2 P-RFO法(Partitioned-RFO)
P-RFO法專用于優化過渡態,效率比RFO更高。RFO對所有方向的步進都使用同一個λ,而在P-RFO中在指向過渡態的方向使用獨立計算的λ(TS),λ(TS)=g(TS)^2/(h(TS)-λ(TS)),應選這個一元二次方程的最大的解,可保證在這個方向上升高能量。其余方向λ的確定和RFO的公式一樣,加和就不再包含指向過渡態的方向,并且選最小的λ解以使這些方向能量降低。這里所謂指向過渡態的方向一般是指最低本征值的方向,在上述RFO方法m為1時也是如此假設(限于其形式RFO也只能用這最低模式),但有時會是其它的非最低的模式,P-RFO也可以將這樣的模式作為指向過渡態的模式,見后文EF方法的討論。2.1.2.3 QA法(Quadratic Approximation,二次逼近)
確定λ的公式是(ΔX(i))^2=∑( -g(i)/(h(i)-λ) )^2=R^2,也就是說每一步移動的距離恰好是置信半徑,這樣步進速度較快。若優化到過渡態,計算λ公式的加和中指向過渡態本征向量的那一項的λ改為-λ,即ΔX(TS)=-g(TS)/(h(TS)+λ)。2.1.2.4 TRIM法(trust-region image minimization,置信區域鏡像最小化)
這個方法假設Hessian本征值最小的方向的梯度和曲率符號與原本相反,而其它方向不變。經過這樣的變化后原來的過渡態位置就成為了能量極小點(過渡態的image),這樣就可以通過優化到極小點而得到過渡態。將TRIM的假設g(TS)'=-g(TS),h(TS)'=-h(TS)代入AH方法的步進公式ΔX(i,λ)=-g(i)/(h(i)-λ),再使分子分母同乘以-1,可知在過渡態方向上的步進公式與其它方向區別僅在于反轉了λ的符號。又由于TRIM也是通過調整λ使步進長度等于為置信半徑,所以在公式的形式上與QA法找過渡態的公式完全一致,QA與TRIM可互為同義詞。通過如上調整AH方法引入的λ可使NR法的步進更有效率、更穩定,還可以通過它改變步進公式在不同方向上的分母項符號,使優化過渡態的初猜點不限于過渡態的二次區域。可直接指定沿某個振動模式升高能量來找過渡態,即便當前點這個方向的Hessian本征值可能是正值,例如從極小點開始跟蹤至過渡態,見后文的EF方法。
2.1.2.5 在高斯中的常見問題
高斯中opt=ts是使用Berny算法來找過渡態,需要提供一個初猜結構。Berny默認的走步的方法是RFO/P-RFO(分別對于優化至極小值/鞍點),若加了Newton選項,則走步基于NR法。每一步對Hessian矩陣的更新方法以UpdateMethod選項指定,尋找極小點時默認用BFGS,找過渡態時默認用Bofill。Berny算法還包括一些細節步驟在內,比如投影掉被凍結的變量、更新置信半徑、設定了線搜索過程中幾種方案等等,詳見手冊opt關鍵字。使用了每步修正Hessian的準牛頓法后,初猜的Hessian矩陣質量明顯影響結構收斂速度,它的不準確容易導致搜索過渡態失敗(在高斯中默認使用價力場得到Hessian)。這種情況需要昂貴的calcfc關鍵字以當前方法水平計算最初的Hessian矩陣,若使用的方法在程序中支持解析二階導數,速度會較好。或者用readfc來讀取包含了Hessian矩陣信息的chk文件,可以先使用低水平方法進行簡正振動分析得到chk文件,再將之讀入作為Hessian矩陣初猜,能夠節約時間,但前提是此勢能面對方法等級不敏感(一般如此)。使用了更準確的初猜后不僅可以增加找到過渡態的成功機率,還有助于在更短的優化步數內達到收斂標準。若使用calcall,則每一點都重新準確計算Hession,會更為可靠,但極為昂貴。
高斯中berny方法尋找過渡態默認每步會檢查Hessian矩陣的本征值是否僅有一個為負,如果不符,就會提示“a wrong sign eigenvalue in hessian matrix”,經常一開始就報錯,原因是初猜結構不符合這個條件,即便這個初猜通過berny方法最終能夠正確優化到過渡態,這時應加noeigentest選項避免本征值符號的檢查,不符合要求也繼續優化,但有一定可能收斂到其它類型駐點。
高斯中默認的置信半徑為0.3 bohr,若優化中步長(RFO/P-RFO步)超過就會輸出“Maximum step size ( 0.300) exceeded in Quadratic search”和“Step size scaled by xxx”,即乘以xxx調小步長至置信半徑內。還有一種考慮更周到的調節方法是在置信半徑代表的球面上優化尋找最佳的位置,這對向極小點優化是默認的,但對于尋找過渡態的優化時需要用nonrscale關鍵字打開。另外可以使用iop(1/8=k)或等價的maxstep=k將置信半徑改為k*0.01 bohr(1 bohr=0.5292埃),調大后往往可以顯著減少收斂步數,很適合勢能面平坦的大體系。注意并不是每一步的步長都固定為k*0.01 bohr,若沒超過置信半徑則步長并不因此改變。尋找極小點時默認為允許動態改變置信半徑,此時iop(1/8)設的就是最初的置信半徑,對于尋找過渡態默認為關閉此功能(相當于用了NoTrustUpdate),可以使用trustupdate關鍵字來打開這個功能。
2.1.3 GDIIS法(Geometry Direct Inversion in the Iterative Subspace)
GDIIS與DIIS原理一致,但用途不同,DIIS優化的是MO組合系數,GDIIS優化的是坐標變量。GDIIS方法趨于收斂到離初始位置最近的駐點,包括過渡態位置。下一步坐標X(new)=X"-H'g",H'代表當前步的Hessian逆矩陣,可見公式形式與NR法是一致的,但是X"與g"不再指當前步的坐標和梯度,而是由之前走過的點的坐標X(k)和梯度g(k)插值得到的,X"=∑c(k)X(k),g"=∑c(k)g(k),代入上式即X(new)=∑c(i)(X(i)-H'g(i)),其中∑是對之前全部走過的點加和。系數c(k)通過使誤差向量r的模最小化得到,r=∑c(k)e(k),并以∑c(k)=1為限制條件。e(k)常見有兩種定義,一種是e(k)=-H'g(k),另一種更常用,是e(k)=g(k),可看出GDIIS利用的是已經搜索過的子空間中坐標與梯度的相關性,通過外推方法估出梯度(即誤差向量)的模盡可能小的坐標,這一點與后述的梯度模方法相似。此方法缺點是由于勢能面復雜,步進中容易被拉到已經過的勢能面的其它駐點而不能到達指定類型駐點,還容易走到類似肩膀形狀的拐點,梯度雖小卻不為0,由于不能達到收斂標準而反復在此處震蕩。另外隨優化步數增加,誤差向量數目逐漸加大,會逐漸出現的誤差向量之間的線性相關,導致偽收斂和數值不穩定問題。在改進的方法中將GDIIS與更可靠的RFO方法結合,比較二者的步進方向和長度,并檢驗GDIIS中的組合系數c,根據一定規則來決定每一步對之前走過的點的保留方式,必要時全部舍去而重新開始GDIIS。Gaussian中用的這種改進的GDIIS方法解決了上述問題同時提高了效率,速度等于或優于RFO方法,尤其是以低水平對勢能面平坦的大體系優化時更為突出。GDIIS計算量小,對Hessian矩陣很不敏感,可以在優化中不更新,也可以用QN法更新來改善性能。此方法自Gaussian98起就是默認的半經驗方法的優化算法,其它方法下也可以用OPT(ts,gdiis)關鍵詞,此時就不再用berny方法而是用GDIIS方法找過渡態。
2.1.4 梯度模優化(gradient norm minimization)
勢能面上的駐點,包括能量極小點、過渡態和高階鞍點的勢能梯度都為0,所以在相應于勢能面的梯度模面上進行優化找到數值為0的點,經過Hessian矩陣本征值符號的檢驗,就能得到過渡態。這相當于把搜索過渡態問題轉化為了能量極小化問題,就有了更可靠的算法可用。(注:梯度模指的是勢能梯度在各個維度分量平方和的平方根,即梯度大小的絕對值)。但是尋找數值更小點的優化方法比如最陡下降法只能找到離初始位置最近的極小點,若找到的梯度模面上的極小點數值大于0則是勢能面肩膀形拐點,沒有什么用處,而這樣的點收斂半徑往往很大,例如圖中在x=2至8的區域內都會收斂到函數拐點,只有提供的初猜結構在x=1和9附近很小的范圍內才會收斂到過渡態,收斂半徑太小,難以提供合理初猜。梯度模面上還多出一些極大點,如x=1.5處,若使用收斂更快的NR法找極小點還容易收斂到這樣沒有意義的點上。基于這些原因,梯度模法很少使用。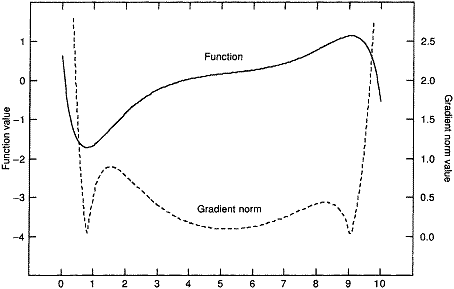
[圖1]原函數與它的梯度模曲線
2.1.5 Dimer方法
Dimer方法是一種高效的定位過渡態的方法。這個方法定義了由兩個點R1和R2組成的一個Dimer,能量和所受勢能力(由原始的勢能面梯度造成受力,下同)分別為E1和E2、F1和F2。兩個點間距為2ΔR,ΔR為定值。這兩點的中間點為R,其受力F(R)=(F1+F2)/2。Dimer的總能量為E=(E1+E2)/2。這個方法的每一步包括平移Dimer和旋轉Dimer兩步。旋轉Dimer:保持R1、R2中點位置R不變作為軸,旋轉Dimer直到總能量E最小。通過推導可知在旋轉過程中,E與R點在dimer方向(R1-R2方向)上的曲率關系C是線性的,即最小化E的過程就是最小化C的過程。所以每一步的Dimer方向都是曲率最小方向,當最終R收斂到過渡態位置時,Dimer就會平行于虛頻方向。
平移Dimer:Dimer根據受力F'移動R的位置,結合不同方法有具體步進方式,如quick-win、共軛梯度法。當C<0(過渡態或高階鞍點的二次區域內),F'等于將F(R)平行于Dimer方向力的分量符號反轉;當C>0(極小點二次區域內),F'等于F(R)平行于Dimer方向力的分量的負值,而沒有垂直于Dimer方向的力,促使Dimer盡快離開這個區域。由于Dimer的方向就是曲率最小的方向,在過渡態二次區域內就是指虛頻方向,在Dimer方法中F'的定義使這個方向以受力相反方向移動以升高能量,而其它方向順著受力方向移動來最小化能量,可看出原理上與NR法相似。費時的計算Hessian矩陣最小本征值以確定提升能量方向的過程被旋轉Dimer這一步代替了,僅需要計算一階導數。Dimer法對初始位置要求很寬松,并不需要在過渡態二次區域內,若在極小點二次區域內就類似于后述的EF方法沿著最小振動模式爬坡。如果在高階鞍點二次區域內,只在曲率最負的虛頻方向沿著受力反向移動,在其它虛頻方向上仍最小化能量,而不會像NR法收斂到高階鞍點。
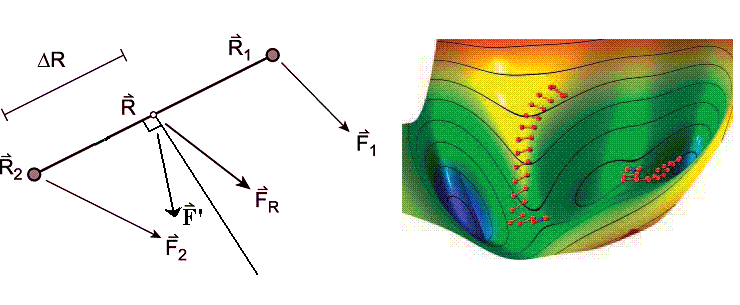
[圖2]右側為Dimer法在Müller-Brown模型勢上面搜索兩個過渡態過程中Dimer走的路徑
勢能面上往往有許多鞍點,Dimer方法還可以做鞍點搜索。通過分子動力學方法給予Dimer一定動能,使之能夠在勢能面上廣闊的區域內運動,根據一定標準提取軌跡中的一些點作為初猜,再執行標準Dimer方法就可以得到許多不同的鞍點。Dimer方法很適合雙處理器并行,兩個點的受力分別由兩個處理器負責,速度可增加將近一倍。
2.2基于反應物與產物結構的算法
2.2.1 同步轉變方法(synchronous transit,ST)
提供合理的初猜結構往往不易,ST方法可以只根據反應物和產物結構自動得到過渡態結構。“同步轉變”這個名字強調的是反應路徑上所有坐標一起變化,這是相對于后面提到的贗坐標法來說的(即只變化指定的坐標,盡管其它坐標優化后坐標也會變化)。ST分為兩種模型,最簡單的就是LST模型(Linear synchronous transit,線性同步轉變),這個方法假設反應過程中,反應物結構的每個坐標都是同步、線性地變化到產物結構。如果反應物、產物的坐標分別以向量A、B表示,則反應過程中的結構坐標可表示為(1-x)*A+x*B,x由0逐漸變到1代表反應進度。注意LST并不是指反應中原子在真實空間上以直線運動,只有笛卡爾坐標下的LST才是如此,在內坐標下的LST,原子在真實空間中一般以弧線運動。以LST的假設,反應路徑在其所用坐標下的勢能面圖上可描述為一條直線,LST給出的過渡態就是這條直線上能量最高點(圖3的點1)。LST的問題也很顯著,其假設的坐標線性變化多數是錯誤的,繪制在勢能面圖上也多數不會是直線,故給出的過渡態也有較大偏差,容易帶兩個或多個虛頻。
比LST更合理的是QST(quadratic synchronous transit,二次同步轉變),它假設反應路徑在勢能面上是一條二次曲線。QST在LST得到的過渡態位置上,對LST直線路徑的垂直方向進行線搜索找到能量極小點A(圖3的點2)。QST給出的反應路徑可以用經過反應物、A、產物的二次曲線來表示,如果這條路徑上能量最大點的位置恰為A,則A就是QST方法給出的過渡態;如果不是,則以最大點作為過渡態。若想結果更精確,可以再對這個最大點向垂直于路徑的方向優化,再次得到A并檢驗,反復重復這個步驟,逐步找到能量更低、更準確的過渡態。
QST方法在計算能力較低的年代曾是簡單快速的獲得過渡態和反應路徑的方法,然而如今看來其結果是相當粗糙的,已極少單獨使用,可以將其得到的過渡態作為AH法的初猜。
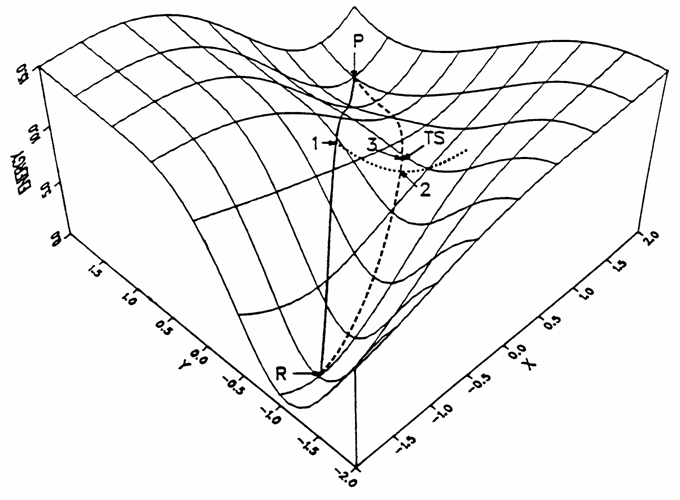
[圖3]LST與QST方法示意圖
2.2.2 STQN方法(Combined Synchronous Transit and Quasi-Newton Methods)
STQN是ST與QN方法的結合(更準確地說是與EF法的結合)。但不要簡單認為是按順序獨立執行這兩步,即認為“先利用反應物和產物結構以ST方法得到粗糙過渡態,再以之作為初猜用QN法精確尋找過渡態”是錯誤的。STQN方法大意是:使結構從低能量的反應物出發,以ST路徑在當前位置切線為引導,沿著LST或QST假設的反應路徑行進(爬坡步),目的是使結構到達假設路徑的能量最高處附近(真實過渡態二次區域附近)。當符合一定判據時就轉換為QN法尋找精確過渡態位置(EF步)。下面介紹具體步驟。先說明后面用到的切線的定義:STQN當中的LST路徑與前面ST部分介紹的LST路徑無異,都是直線,切線T在優化中是不變的,就是反應物R指向產物P的單位向量。STQN方法中的QST路徑定義與ST方法介紹的不同,走的不是二次曲線而是圓形的一段弧,如圖4所示。這個圓弧經過R、P以及優化中的當前步位置X,切線就是圓在X處的單位切線向量,圓弧和切線在每一步都是變化的。雖然QST路徑比LST更為合理,但對于QSTN方法,QST路徑在收斂速度和成功機率上的優勢并不顯著。
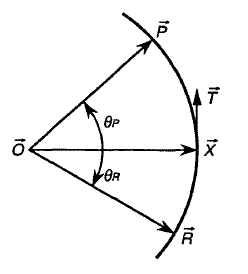
[圖4]STQN對QST路徑的定義
STQN每一步執行內容如下:(1)首先重新計算或用QN法更新Hessian。(2)按上述方法計算當前位置處的切線。(3)決定這一步是爬坡步還是EF步。如果是優化的第前兩步,則一定認為是爬坡步,因為此時離過渡態區域還較遠,應當先爬坡。如果是第3、4步,則估算出在切線方向的位移,超過一定標準就是爬坡步,否則說明爬得差不多了就進入EF步找過渡態。如果是第5步之后,一般已離過渡態區域較近,故一定認為是EF步。(4)如果是爬坡步,則在切線方向上移動(將切線方向作為EF方法所跟蹤的振動方向來計算位移大小)。如果是EF步,首先計算Hessian各個本征向量的與切線重疊情況,如果有重疊大于0.8的本征向量,則以EF法跟蹤本征值最大的本征向量來移動,相當于繼續向上爬。如果沒有大于0.8的,就跟蹤最小本征值的本征向量移動來尋找過渡態。(5)步長長度若大于標準則調小,默認0.3 bohr。(6)根據預置受力、位移標準判斷是否已收斂,收斂則結束循環。
注意,ST方法中具體包含LST和QST兩種方法,STQN也用到了LST和QST兩種反應路徑的假設。高斯中的LST方法指的是ST中的LST方法,而QST2/3指的是利用QST路徑假設的STQN方法,它們原理上截然不同,不要混淆。高斯中的QST2只需輸入反應物和產物結構,通過在冗余內坐標下反應物與產物結構間插值得到STQN的初始步結構X。QST3需額外輸入猜測的過渡態,它直接作為X,一般比QST2效果更好。對于經驗不足的用戶,用STQN方法往往比只提供過渡態初猜的方法更為適合。注意產物和反應物應當使用同樣方法同樣基組進行優化,如果是多分子比如A+B=C+D這樣的反應,應當優化A和B/C和D的復合物作為輸入的產物/產物,而不是單獨優化A、B然后拼到一起,因為形成范德華復合物后孤立的分子會有一定構象改變,能量也低于它們孤立狀態的加和。
2.2.3 贗坐標法(pseudo reaction coordinate)
也稱為坐標驅動法(Coordinate Driving)。這個方法在高斯中就是柔性掃描(Relaxed Scan),即掃描一個變量,但每一步對其它變量自動進行優化,每一步得到的結構就是在這個變量為一定值情況下的最優結構。贗坐標法掃描的是反應物轉變到產物過程中的關鍵坐標,比如掃描化學鍵斷裂/生成反應中的鍵長。掃描的結果就是近似的IRC,可以再將能量最高點作為初猜找過渡態,或者用更小的步長再次掃描能量最高點附近找更精確的過渡態結構。這個找過渡態方法實際上用的是能量極小化優化過程,由于這樣的算法比尋找過渡態的算法更為穩健,所以贗坐標法是頗可靠的,其它方法失敗時可考慮這種方法。這個方法缺點是費時間,而且不適合通向過渡態路徑中反應區域涉及多個坐標變化的反應過程,因為自定義掃描的內容很難全面、準確考慮到這些坐標變量的變化,結果難以說明問題,沒有考慮進去的關鍵變量容易產生滯后效應(hysteresis effect)。比如乙烷由交叉構象變化到另一個交叉構象,需要經歷重疊構象的過渡態,會涉及到三個HCCH二面角同時由60度變化到0度,如果用贗坐標法只掃描其中一個HCCH由60度變到0度,則每一步其它兩個HCCH角一定會大于這個掃描的二面角,與實際不符。這是因為這兩個角越小,分子的能量越高,每一步自動優化的時候它們更傾向于保持在大角度。最終到達過渡態時,所掃描的二面角到達了0度,另外兩個二面角卻大于0度,說明它們的運動比實際的過程滯后了。由于滯后效應,從反應物和產物兩個方向掃描同相同的坐標,得到的路徑也不同。上述簡單的反應此方法滯后效應尚且嚴重,對于復雜變化,這種效應導致的問題更難以預測。故此方法確定的IRC、過渡態不可靠,只建議對簡單的反應使用這種方法,掃描變量的選擇注意避免滯后效應。
在高斯中此方法可以使用opt=modredundant或Opt=Z-matrix結合分子結構部分標記的掃描變量來實現。例如使用opt=modredundant并在分子結構末尾寫上A 3 2 1 S 10 1.000000來指定3 2 1原子組成的角度進行柔性掃描,共10步,每步1.0度。如果不熟悉,也可以很方便地在GaussView里的冗余坐標編輯器里面添加要柔性掃描的變量。
如果只執行常規的某個變量的掃描,比如高斯中的scan來找能量最高點作為初猜結構,對于簡單體系可行,但對于復雜體系,這樣忽略了此變量的變化導致分子其它部分結構的馳豫,如此得到的能量最高點作為過渡態初猜很不可靠,因為勢能中摻入了不合理的結構造成的能量升高,使勢能曲線形狀改變。
2.2.4 DHS方法(Dewar-Healy-Stewart,亦稱Saddle方法)與LTP方法(Line-Then-Plane)
DHS方法中第一步將反應和產物分別作為A點和B點,確定哪個點能量低,比如A比B低,就把A點的結構向B點稍微做調整(~5%)得到A',然后限制變量空間中A'與B的距離不變(即在超球面上)對A'進行優化得到A''。將A''與B當作下一步的起始點A與B,重復上述方法。這樣反復進行迭代,若以序號n代表第n次得到的A''或B'',會依次得到例如A''(1)、A''(2)、B''(1)、A''(3)......直到A與B十分接近時才停止迭代,此位置就是過渡態。將得到的全部A''(n)按序號n依次連接,B''(n)也按序號依次連接,再將序號最大的A''(n)與B''(n)連接,得到的就是近似的IRC。LTP與DHS方法基本一致,不同的是每步是在垂直于A'與B連線的超平面上優化。DHS方法雖然可以很快地走到過渡態附近的位置,但是越往后每步的AB距離縮近也越少,故并不能有效率地貼近過渡態。然而每步的在連線上調整的距離不可過大,否則可能造成一側的點跨過過渡態勢壘跑到另一側得到錯誤結果。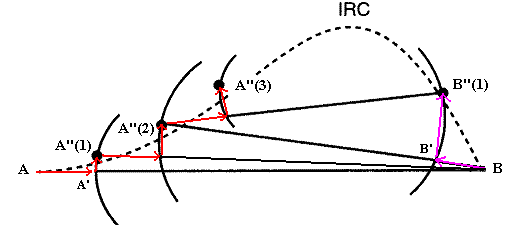
[圖5]DHS方法示意圖
2.2.5 Ridge方法
第一步時將反應物、產物作為A點和B點,在其LST的路徑上找到能量最大點C,然后在AC與BC直線上相距C為s的位置上分別設一點A'和B',將A'與B'分別沿著此處勢能面負梯度優化p距離,將得到的A''與B''作為下一步的A和B。反復進行這個步驟,收斂后C的位置就是過渡態位置。s和p是計算過程中動態調節的參數,對結果影響較大,它們應當隨C逐漸接近過渡態而減小,可設若當前步的C能量高于上一步的C,則減小p至原先一半;若s與p的比值大于某個數值,s也減半。Ridge方法的缺點是接近過渡態時效率較低,可以當C進入過渡態二次區域后改用QN法來加快收斂。也可以結合DIIS法,速度比原先有一半以上的提升,效率有時還高于基于二階導數的方法,而且在某些勢能面非常平坦的體系比二階導數方法更可靠。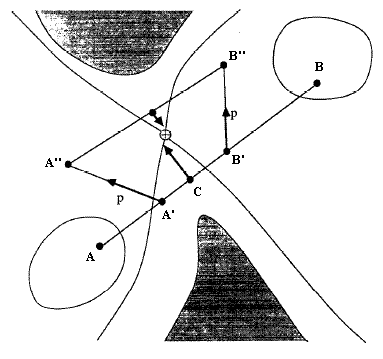
[圖6]Ridge方法示意圖
2.2.6 Step-and-Slide方法
使產物和反應物的結構同時順著LST描述的路徑相對移動(step步),直到它們的能量都等于某個預先設定的能量,然后讓這兩個結構在它們當前所在的勢能等值面上滑動(slide步),使二者結構在坐標空間中的距離最小。重復上述step和slide步驟,最終當兩個結構碰上,這個位置就是過渡態。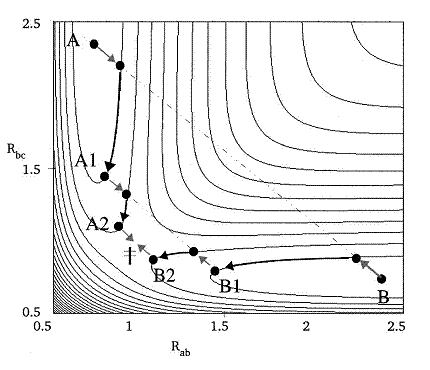
[圖7]Step and Slide方法示意圖
2.2.7 Müller-Brown方法
見下文IRC算法相應部分2.2.8 CI-NEB、ANEBA方法
見下文“尋找過渡態的chain-of-state方法”相應部分2.3 基于反應物結構的算法
2.3.1 最緩上升法(least steep ascent,shallowest ascent)
由反應物結構到達過渡態結構的過程是沿著勢能面最容易行進的路徑進行的(不考慮動力學問題),這個途徑一般比其它方向要緩和,所以由反應物結構開始,沿著勢能面最緩的方向逐漸往上爬,往往可以沿著MEP到達過渡態。但要注意這條路徑時常與從過渡態沿最陡下降路徑所走出的MEP并不一致,因此原理上此法不能保證一定能到達過渡態。圖8描述的是LEPS勢結合諧振勢的勢能面,最緩上升法所走的黑色粗曲線嚴重不符合實際MEP(黑點所示路徑),而且曲線是中斷的。此法也可能走到與此平衡結構相連的其它過渡態,而非預期的過渡態。還容易因為步長問題導致走到中途時跑到另外一條錯誤路徑上,雖然設小步長能得到解決,但是需要花費更長時間。因為種種問題,這個方法使用較少。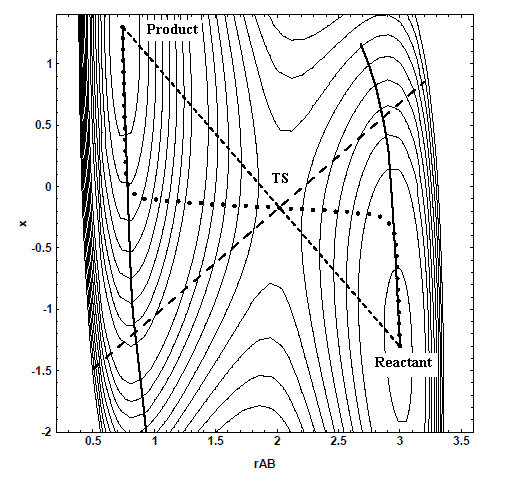
[圖8]勢能面上最緩上升法所走的路徑(黑色粗曲線)
2.3.2 本征向量/本征值跟蹤法(eigenvector/eigenvalue following,EF。也稱mode walking/mode following/Walking up valleys)
名字中的本征向量、本征值是指Hessian矩陣的本征向量和本征值,經過質量加權后就對應于簡正振動模式和相應的力常數,所以也叫模式跟蹤。由于平衡結構越過勢壘發生反應的能量主要來自分子某振動模式提供的動能,由此可以想象,由穩定結構沿著此振動矢量方向步進,就能夠找到過渡態,經歷的路徑就是反應路徑。這種方法需要首先對平衡結構進行振動分析,由用戶最初指定一個可能指向過渡態的振動模式。由于由平衡態出發,通向過渡態路徑勢能面平緩,此方向曲率一般小于其它方向,故一般跟蹤力常數最小的振動模式(高斯中默認),這也叫最低模式(Low-Mode),這個模式的力常數一開始是正值(頻率為實數),經過勢能面拐點后變為負數(頻率為虛數),直至到達過渡態。每走一步后重新計算Hessian矩陣獲得新的振動模式和對應力常數,如果跟蹤的是最低的模式,仍取力常數最小的模式繼續跟蹤;如果跟蹤的是其它振動模式,就取與上一步所跟蹤的振動模式重疊最大的模式繼續跟蹤。重復執行,直到符合收斂標準為止。如果一個結構涉及到多個過渡態,則跟蹤不同的本征向量有可能得到不同的過渡態,即便所跟蹤的不是最低模式,當接近過渡態后也會成為最低的模式。此方法也可以直接由過渡態初猜結構開始跟蹤,或者說EF方法是一種不需要初猜在過渡態二次區域內的尋找過渡態的方法。由穩定結構通過EF方法跟蹤至過渡態相對與直接給出初猜顯然更為費時,但對于不能預測過渡態結構的情況下往往是有用的。LMOD法搜索構象也是基于這一原理,不斷地根據低頻振動方向越過構象轉變的過渡態到達新的構象。
最初的EF方法只是簡單地沿所跟蹤的振動模式移動來升高能量。高斯中opt=(EF,TS)方法還使結構同時在其余方向上沿能量更低的方向移動,其實它用的就是已介紹的P-RFO法,所跟蹤的模式用獨立計算的λ的最大解,其它的模式使用相同的另外計算的λ的最小解。由于Berny方法尋找過渡態已經包含了P-RFO步,所以EF方法實際上也已經包含在內了,除非要用到跟蹤特定模式等功能時才有使用的必要。
2.3.3 ARTn(activation-relaxation technique nouveau)
此方法主要用于研究無序材料的在能量面上由極小點穿過過渡態到達其它極小點的過程,解決由于勢壘高而難以用MD和MC方法研究的問題。方法分兩步,(1)將初始結構由極小點位置激活并收斂到過渡態(activation步),(2)由過渡態通過常規的能量極小化算法尋找極小點(relaxation步)。(1)中的每一步中在任意方向上移動結構,然后在垂直于走過的路徑方向的超平面上做能量極小化,反復執行,直到Hessian矩陣出現一個負本征值為止。之后進入收斂至鞍點的步驟,在最小本征值的方向上沿受力反方向移動,其余方向根據受力移動,最終將找到一階鞍點。由于大體系Hessian矩陣本征值求解困難,此方法中使用Lanczos算法快速求解最低本征值和本征向量。ART法可以獲得與初始極小點相連的許多過渡態。2.3.4 梯度極值法(Gradient extremal,GE)
梯度極值路徑連接的是每一個能量等值線(高維情況為超曲面)上的梯度的模|g|為極大或極小值的點(相對于同一等值線上的其它點的梯度模來說)。因為勢能面的每一點的梯度垂直于此點等值線的切線,故梯度模極值點的位置相當于垂直于等值線方向上等值線間隔比處在相同等值線上相鄰的點更遠或更近。|g|的極值與g^2一致,設勢能函數為f,限制所在等值線能量為一常數k,通過拉格朗日乘子法求g^2的極值▽[g^2-2λ(f-k)]=0,執行微分后寫成Hg=λg,可知梯度極值點的梯度方向等于此點Hessian矩陣某一本征向量。由于勢能面上每個駐點必有一條或多條梯度極值路徑通過而互相構成網絡(但任意駐點間不一定有梯度極值路徑直接相連),所以系統地跟蹤梯度極值路徑是一種獲得勢能面上全部駐點的方法,目前已有幾種跟蹤算法,然而即便對于簡單體系,梯度極值路徑數目也極多,尤其是包含對稱性情況下。由極小點跟蹤梯度極值路徑也能夠用于尋找過渡態,但極小點未必與過渡態通過梯度極值路徑直連,且此方法并不能控制要尋找哪類駐點,故為了尋找過渡態可能需要從多個其它駐點跟蹤多個梯度極值路徑,計算量很大,所以單純為了尋找過渡態而使用這種方法不切實際。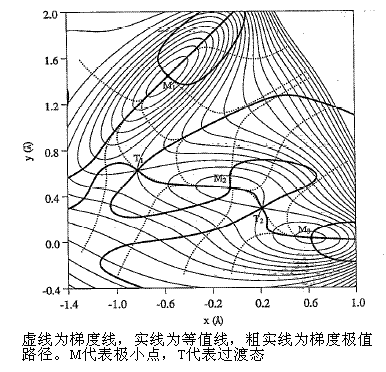
[圖9]梯度極值路徑示意圖
2.3.5 約化梯度跟蹤(reduced gradient following,RGF)
這個方法同梯度極值法一樣可以得到包括過渡態、極小點在內的各種駐點。設勢能面為N維,此方法將跟蹤N條路徑,其中第i條(i=1,2,3...N)路徑只有在第i維上梯度不為0,而其它N-1個維度上皆為0,故稱為約化梯度。這樣的路徑交匯的位置,就是所有維度上梯度皆為0的位置,即駐點。例如簡單的二維情況E(x,y)=x^3+y^3-6xy,跟蹤的RGF方程就是Ex(x,y)=3x^2-6y=0和Ey(x,y)=3y^2-6x=0,前者僅y方向梯度不為0,后者僅x方向梯度不為0,相交得到的駐點為一個一階鞍點和一個極小點。也可以使用原始坐標組合的正交坐標系,例如跟蹤僅x+y和僅x-y方向上梯度不為0的兩條路徑。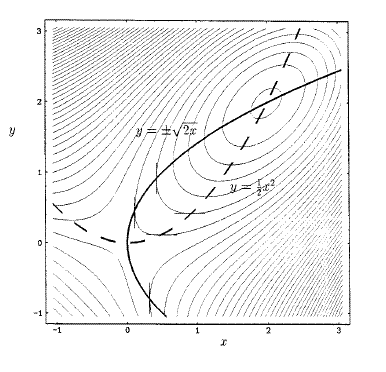
[圖10]x^3+y^3-6xy面上約化梯度路徑示意圖
跟蹤約化梯度的步進算法是第m點的坐標x(m+1)=x(m)+StL*x'(m)/|x'(m)|。StL是步長,x'(m)/|x'(m)|代表路徑切線方向單位向量。x'可以通過H'x'=0方程以QR分解法獲得,其中H'與Hessian矩陣唯一不同的是,若當前跟蹤的是僅第k維梯度不為0的約化梯度路徑,則H'沒有Hessian矩陣的第k行。一般起始步由某駐點開始,此步準確計算Hessian,步進過程中Hessian可用前述的DFP方法修正。每步檢驗所跟蹤方向上的朝向下一個駐點的牛頓步步長,若小于標準則停止,并且再精確計算一次Hessian以確認此駐點是什么類型。每次走步的結果如果在數值上與“僅某維度上梯度為0”條件符合較好,可以動態增加步長,類似AH法的置信半徑概念,如果相差較大,則調用校正步(后期方法將校正步合并入步進步,改善了效率和穩定性)。
這個方法計算量也很大,而且也無法指定要搜索的駐點的類型,所以不適合獨立用作尋找過渡態。
2.3.6 等勢面搜索法(Isopotenial Searching)
如果將反應物位置附近的勢能面比做一個湖,這個方法可以看作逐漸往湖里面灌水,由于過渡態能量比周圍地方更低,所以隨著水位(勢能)逐漸升高,水最先流出來的地方就是過渡態。繼續灌水,隨著水位繼續升高,還可以找到其它能量更高的過渡態。具體實現的方法是:首先最小化反應物的能量E0,在反應物位置附近設置一些測試點,可以隨機也可以根據經驗設定,作為“水位”來檢測是否已到達過渡態能量。然后設定目標能量E(target),一般高于E0幾百KJ/mol。計算那些測試點的能量和勢能梯度,檢查其能量與E(target)的差的絕對值,若大于10KJ/mol,即沒達到目標水位,就讓它們沿著梯度方向行進以提升能量,之后再次檢查是否符合條件,直到小于10KJ/mol,即已到達目標水位,就對這些點進行人工的檢查,包括結構、成鍵分析等,考察在E(target)時是否已經達到或超過了過渡態的能量。如果找到了過渡態,就調整這些點的位置繼續找別的過渡態;如果未找到,就提高E(target)并且調測試點整位置以增大找到過渡態的概率,然后再沿著梯度方向提升測試點的能量并進行接下來的檢測,反復如此。
上述提到的“調整點的位置”有很多算法,但主要都是使那些測試點在垂直于梯度,即在等值面上移動。因為測試點無法密集覆蓋整個等勢面,受計算能力制約其數目有限的,很難有哪個點隨著E(target)的提升而移動后恰好落在過渡態的位置。直到E(target)提升到有測試點可判斷為過渡態時,其能量一般已高出實際過渡態很多。所以使用此方法得到的過渡態能量與初始點位置和調整點位置的算法都有很大關系,一般都顯著偏高,甚至不能找到過渡態,可嘗試以不同初始位置和調整算法重新執行以改善結果。等勢面搜索法適合在只有反應物結構而難以預測過渡態和產物結構的情況下尋找過渡態,例如預測質譜中分子的可能裂解的方式,有時還可能找到全新未曾考慮到的反應機理。但是此方法的結果很粗糙,而且計算量極大,尤其是大分子的高維勢能面,有限的測試點很容易漏掉許多重要過渡態。
2.3.7 球形優化(Sphere optimization)
在幾何參數的變量空間上,以反應物或產物為中心,在不斷增加半徑的超球面上做能量最小化。將相鄰球面上得到的能量極小點相連接,就得到一條由反應物或產物為起點的低能量的路徑,可做為IRC(未必正確,考慮圖8的勢能面),并由此找到過渡態。如果每個球面上可以找到多個極小點,則連接后有可能得到多條反應路徑。此法若以坐標驅動法為類比,此方法就是對幾何參數空間中反應物或產物結構代表的點的距離進行柔性掃描。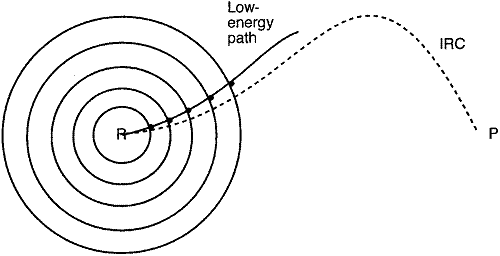
[圖11]球形優化示意圖
2.4 全勢能面掃描
當一切方法都不能找到過渡態,全勢能面掃描是最終途徑。由于掃描得到的勢能面格點是離散的,可通過插值提高格點密度以增加精度。得到勢能面后,就可以通過一些算法找到過渡態,例如用這些點擬合出解析表達式,然后用標準微分方法找過渡態。但全勢能面掃描極為昂貴,內坐標下需要計算X^(3N-6)次(X代表每個變量掃描步數),只限于反應中僅涉及幾個自由度的勢能面掃描,往往不得不考慮更低級的方法如半經驗或者分子力學,變量稍多的體系則完全不能實現。全勢能面掃描的結果還提供了過渡態位置以外結構的信息,例如可以用于研究反應路徑、用于構象搜索等。3.過渡態相關問題
3.1 無過渡態的反應途徑(barrierless reaction pathways)
并非所有反應途徑都需要越過勢壘,這類反應在很低的溫度下就能發生,盲目找它們的過渡態是徒勞的。常見的包括自由基結合,比如甲基自由基結合為乙烷;自由基向烯烴加成,比如甲基自由基向乙烯加成成為丙基自由基;氣相離子向中性分子加成,比如叔碳陽離子向丙烯加成。等等。3.2 Hammond-Leffler假設
過渡態在結構上一般會偏向反應物或者產物結構一邊。Hammond-Leffler假設對預測過渡態結構往哪個方向偏是很有用的,意思是反應過程中,如果兩個結構的能量差異不大,則它們的構型差異也不大。由此可知對于放熱反應,因為過渡態能量與反應物差異小,與產物差異大,故過渡態結構更偏向反應物,相反,吸熱反應的過渡態結構更偏向產物。所以初猜過渡態結構應考慮這一問題。3.2 對稱性問題
如果已經明確地知道過渡態是什么對稱性,而且對稱性高于平衡態對稱性,且可以確信在這個高對稱性下過渡態是能量最低點,則可以強行限制到這個對稱性之后進行幾何優化,幾何優化算法比尋找過渡態算法方法更可靠。比如F+CH3F-->FCH3+F這個SN2反應,過渡態就是傘形翻轉的一刻,恰為高對稱性的D3h點群,而反應路徑上的其它結構對稱性都比它低,所以在D3h點群條件下優化,得到的能量最低點就是過渡態。如果過渡態對稱性不確定,則找過渡態計算的時候不宜設任何對稱性,否則若默認保持了平衡態下的對稱性,得到的此對稱下的過渡態并不是真正的過渡態,容易得到二階或高階鞍點。
3.3 溶劑效應
計算凝聚態條件下過渡態的性質,必須考慮溶劑效應,它明顯改變了勢能面。一般對過渡態的結構影響較小,但對能量影響很大。有時溶劑效應也會改變反應途徑,或產生氣相條件下沒有的勢壘。溶劑條件下,上述尋找過渡態的方法依然適用。應注意涉及到與溶劑產生氫鍵等強相互作用的情況,隱式溶劑模型是不適合的,需要用顯式溶劑考察它對過渡態的影響,即在輸入文件中明確表達出溶劑分子。3.4 計算過渡態的建議流程
一般建議的流程是:1 用中等計算級別找過渡態,如B3LYP/6-31G*。
2 用相同水平對上一步找到的過渡態做振動分析,檢驗是否僅有一個虛頻,以及觀看其振動模式的動畫來考察振動方向是否連接反應物與產物結構。有必要時可以做IRC進一步檢驗。
3 用高級別方法(如雙雜化泛函或CCSD(T)結合def2-TZVP等中/高質量基組)對第1步得到的過渡態結構計算能量。
另外,如果對B3LYP/6-31G*這樣級別的過渡態的精度還不夠滿意(雖然通常已經夠了),可以以這個級別的過渡態為初猜結構,改用更好的方法和基組去進一步優化過渡態結構。
4.內稟反應坐標(intrinsic reaction coordinate,IRC)
MEP指的是勢能面上,由一個點到達另一個點的能量最低的路徑,滿足最小作用原理。若質量權重坐標下的MEP連接的是反應物、過渡結構和產物,則稱為IRC。所謂質權坐標在笛卡兒坐標下即r(i,x)=sqrt(m(i))*R(i,x),m(i)為i原子質量,R(i,x)為i原子原始x方向坐標,同樣有r(i,y)、r(i,z)。IRC描述了原子核運動速度為無限小時,質權坐標下由過渡態沿著勢能負梯度方向行進的路徑(最陡下降路徑),其中每一點的負梯度方向就是此處核的運動方向,在垂直于路徑方向上是能量極小點。注意質量權重和非權重坐標下的路徑是不一樣的。IRC基本上可看作0K時的實際在化學反應中原子核所走的路徑(但這并不嚴格,因為由于振動零點能的關系,即便0K下也有核運動故會略微偏離IRC),溫度較低時IRC也是一個很好的近似。但是當溫度較高,即核動能較大時,實際反應路徑將明顯偏離IRC,而趨于沿最短路徑變化,即便經歷的是勢能面上能量較高的的路徑,這時就需要以動力學計算的平均軌跡來表征反應路徑。
5.IRC算法
5.1 最陡下降法(Steepest descent)
最簡單的獲得IRC的方法就是固定步長的最陡下降法,由過渡態位置開始,每步沿著當前梯度方向行進一定距離直到反應物/產物位置,也稱Euler法。由于最陡下降法及下文的IMK、GS等方法第一步需要梯度,而過渡態位置梯度為0,所以第一步移動的方向沿著虛頻方向。最陡下降方法與IRC的本質相符,但是此法實際得到的路徑是一條在真實IRC附近反復震蕩的曲折路徑,而非應有的平滑路徑,對IRC描述不夠精確。雖然可以通過更小的步長得以一定程度的解決,但是太花時間,對于復雜的反應機理,需要更多的點。也可以通過RK4(四階Runga-Kutta)來走步,比上面的方法更穩定、準確,但每步要需要算四個梯度,比較費時。5.2 IMK方法(Ishida-Morokuma-Kormornicki)
它是最陡下降法的改進,解決其震蕩問題。首先計算起始點X(k)的梯度g(k),獲得輔助點X'(k+1)=X(k)-g(k)*s,其中s為可調參數。然后計算此點梯度g'(k+1),在g(k)與-g'(k+1)方向的平分線上(紅線所示)進行線搜索,所得能量最小點即為X(k+1),之后再將X(k+1)作為上述步驟的X(k)重復進行。整個過程類似先做最陡下降法,然后做校正。此方法仍然需要相對較小的步長,獲得較精確IRC所需計算的點數較多。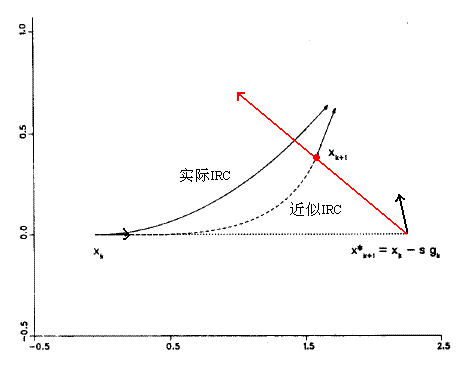
[圖12]IMK方法示意圖
Schmidt,Gordon,Dupuis改進了IMK的三個細節,使之更有效率、更穩定。(1)將X'(k+1)的確定方式改為了X(k)-g(k)/|g(k)|*s,即每一步在負梯度方向上行進固定的s距離,與梯度大小不再有關。(2)線搜索步只需在平分線上額外計算一個點的能量即可,這個點和X'(k+1)點的能量以及g'(k+1)在此平分線上的投影三個條件作聯立方程即可解出曲線方程,減少了計算量。IMK原始方法則需要在平分線上額外計算兩個點的能量與X'(k+1)的能量一起擬和曲線方程。(3)第一步在過渡態位置的移動距離Δq如此確定:ΔE=k*(Δq^2)/2,k為虛頻對應的力常數,ΔE為降低能量的期望值(一般為0.0005 hartree),這樣可避免在虛頻很大的鞍點處第一步位移使能量降低過多。
5.3 Müller-Brown方法
這是通過球形限制性優化找IRC的方法。首先將過渡態和能量極小點位置定義為P1和P2,由P1開始步進,當前步結構以Q(n)表示。每一步,在相距Q(n)為r距離的超球面上用simplex法優化獲得能量極小點Q'(圖中綠點),優化的起始點是Q(n-1)Q(n)與Q(n)P2方向的平分線b上距Q(n)為r距離的位置S(紅點)。若Q(n)Q'與Q(n)P2的夾角較小,則Q'可當作是下一步位置Q(n+1)。如此反復,直到符合停止標準,比如下一步能量比當前更高(已走過頭了)、與P2距離已很近(如小于1.2r)、或者與P2方向偏離太大(P1與P2點通過此法無法找到IRC)。最終所得到全部結構點依次相連即為近似的IRC,減小步長r值可使結果更貼近實際IRC。基于此方法也可以用于尋找過渡態,先將反應物和產物作為P1和P2,將二者距離的約2/3作為r,由其中一點在P1-P2連線上相距其r位置為初始位置進行球形優化得到O點,在O與P1、O與P2上也如此獲得P1'與P2',根據P1、P1'、O、P2'、P2的能量及之間距離信息以一定規則確定其中哪兩個點作為下一步的P1和P2,確定新的P1和P2后重復上述步驟,直至P1與P2十分接近,即是過渡態。此方法計算IRC可以步長可設得稍大,第一步不需要費時的Hessian矩陣確定移動方向,缺點是獲得的路徑曲率容易有問題,對于曲率較大的反應路徑需要減小步長。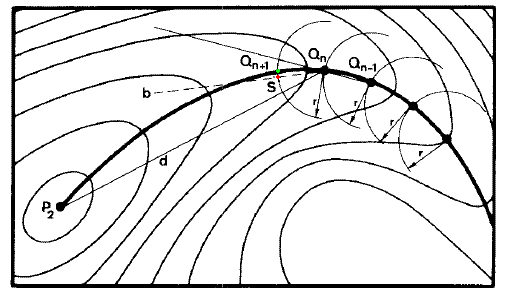
[圖13]Müller-Brown方法示意圖
5.4 GS(Gonzalez-Schlegel)方法
這是目前很常用,也是Gaussian使用的方法,見圖14。首先計算起始點X(k)的梯度,沿其負方向行進s/2距離得到X'(k+1)點作為輔助點。在距X'(k+1)點距離為s/2的超球面上做限制性能量最小化,找到下一個點X(k+1)。因為這個點的負梯度(黑色箭頭)在弧方向上分量為0,故垂直于弧,即其梯度方向在X'(k+1)到X(k+1)的直線上。這必然可以得到一段用于描述IRC的圓弧(虛線),它通過X(k)與X(K+1)點,且在此二點處圓弧的切線等于它們的梯度方向,這與IRC的特點一致,這段圓弧可以較好地(實線)。之后再將X(k+1)作為上述步驟的X(k)重復進行。GS方法對IRC描述得比較精確,在研究反應過程等問題中,由于對中間體結構精度有要求,GS是很好的選擇,而且用大步長可以得到與小步長相近的結果,優于IMK、Müller-Brown等方法。若只想得到與過渡態相連的反應物和產物結構,或者粗略驗證預期的反應路徑,對IRC精度要求不高,使用最陡下降法往往效率更高,盡管GS可以用更大步長,但每步更花時間。
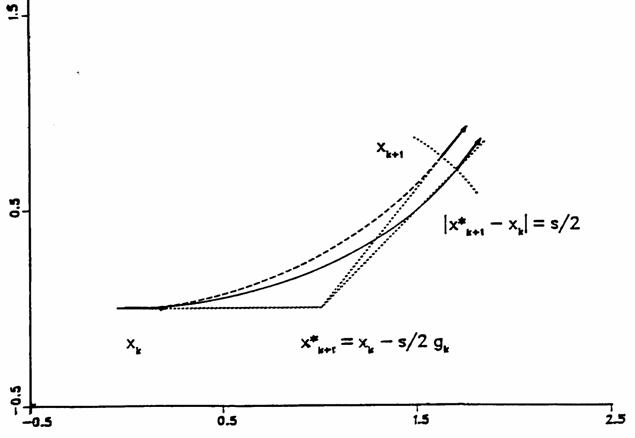
[圖14]GS方法示意圖
除上述外,IRC也可以通過已提及的EF、最緩上升法、球形優化等方法得到,它們的好處是不需要事先知道過渡態的結構。贗坐標法除了簡單的反應以外,只能得到近似的IRC,由于結構的較小偏差會帶來能量的較大變化,容易引入滯后效應,所以這樣得到的勢能曲線難以說明問題。
6. chain-of-states方法
這類方法主要好處是只需要提供反應物和產物結構就能得到準確的反應路徑和過渡態。首先在二者結構之間以類似LST的方式線性、均勻地插入一批新的結構(使用內坐標更為適宜),一般為5~40個,每個結構就是勢能面上的一個點(稱為image),并將相鄰的點以某種勢函數相連,這樣它們在勢能面上就如同組成了一條鏈子。對這些點在某些限制條件下優化后,在勢能面上的分布描述的就是MEP,能量最高的結構就是近似的過渡態位置。
6.1 Drag method方法
這個方法最簡單,并不是嚴格的chain-of-states方法,因為每個結構點是獨立的。插入的結構所代表的點均勻分布在圖8所示的短虛線上,也可以在過渡態附近位置增加點的密度。每個點都在垂直于短虛線的超平面上優化,在圖中就是指平行于長虛線方向優化。這種方法一般是奏效的,但也很容易失效,圖8就是一例,優化后點的分布近似于從產物和反應物用最緩上升法得到的路徑(黑色粗曲線),不僅反應路徑錯誤,而且兩段不連接,與黑色小點所示的真實MEP相距甚遠(黑色點是用下文的NEB方法得到的)。目前基本不使用此方法。6.2 PEB方法(plain elastic band)
這是下述Chain-of-state方法的基本形式。也是在反應物到產物之間插入一系列結構,共插入P-1個,反應物編號為0,產編號物為P。不同的是優化不是對每個點孤立地優化,而是優化一個函數,每一步所有點一起運動。下文用∑[i=1,P]X(i)符號代表由X(1)開始加和直到X(P)。PEB函數是這樣的:S(R(1),R(2)...R(P-1))=∑[i=1,P-1]V(R(i)) + ∑[i=1,P]( k/2*(R(i)-R(i-1))^2 )。其中R(i)代表第i個點的勢能面上的坐標,V(R(i))是R(i)點的能量,k代表力常數。優化過程中反應物R(0)和產物R(P)結構保持不變,優化此函數相當于對一個N*(P-2)個原子的整體進行優化,N為體系原子數。優化過程中,式中的第一項目的是讓每個點盡量向著能量極小的位置移動。第二項相當于將相鄰點之間用自然長度為0、力常數為k的彈簧勢連了起來,目的是保持優化中相鄰點之間距離均衡,避免過大。當只有第一項的時候,函數優化后結構點都會跑到作為能量極小點的反應物和產物位置上去而無法描述MEP,這時必然會有一對兒相鄰結構點距離很大。當第二項出現后,由于此種情況下彈簧勢能很高,在優化中不可能出現,從而避免了這個問題。drag method法在圖8中失敗的例子中,也有一對兒相鄰結構點距離太遠,所以也不會在PEB方法中出現。簡單來說,PEB方法就是保持相鄰結構點的間距盡量小的情況下,優化每個結構點位置。可以近似比喻成在勢能面的模型上,將一串以彈簧相連的珠子,一邊掛在反應物位置,另一邊掛在產物位置,拉直之后松手,這串珠子受重力作用在模型上滾動,停下來后其形狀可當作MEP,最高的位置近似為過渡態。
但是PEB方法的結果并不能很好描述MEP。圖15描述的是常見的A、B、C三原子反應的LEPS勢能面,B可與A或C成鍵,黑色弧線為NEB方法得到的較真實的MEP。左圖中,在過渡態附近PEB的結構點沒有貼近MEP,得到的過渡態能量過高,稱為corner-cutting問題。這是因為每點間的彈簧勢使這串珠子僵硬、不易彎曲,由圖15右圖可見,R(i)朝R(i-1)與R(i+1)方向都會受到彈簧拉力,其合力牽引R(i),使R(i-1)、R(i)、R(i+1)的弧度有減小趨勢。如果將彈簧力常數減小以減弱其效果,就會出現圖15中間的情況,雖然結構點貼近了MEP,但相鄰點間距沒有得到保持,過渡態附近解析度很低,錯過了真實過渡態,若以能量最高點作為過渡態則能量偏低,這稱為sliding-down問題。可見彈簧力常數k的設定對PEB結果有很大影響,為權衡這兩個問題只能取折中的k,但結果仍不準確。
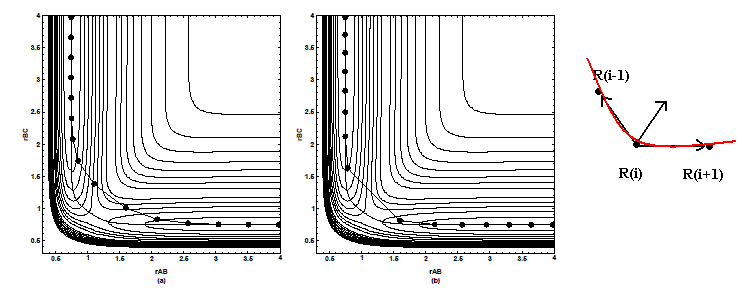
[圖15]LEPS勢能面上不同k值的PEB結果
6.3 Elber-Karplus方法
與PEB函數定義相似。第一項定義為1/L*∑[i=1,P-1]( V(R(i))*d(i,i-1) ),其中L為鏈子由0點到P-1點的總長,d(i,i+1)為R(i)與R(i+1)的距離,此項可視為所有插入點總能量除以點數,即插入點的平均能量。第二項為γ*∑[i=1,P](d(i,i-1)-<d>)^2,其中<d>代表相鄰點的平均距離,是所有d(i,j)的RMS。此項相當于將彈簧自然長度設為了當前各個彈簧長度的平均值,由γ參數控制d(i,j)在平均值上下允許的波動的范圍。此方法最初被用于研究蛋白質體系的構象變化。6.4 SPW方法(Self-Penalty Walk)
在Elber-Karplus方法的基礎上增加了第三項互斥項,∑[i=0,P-1]∑[i=j+1,P-1]U(ij),其中U(ij)=ρ*exp(-d(i,j)/(λ*<d>)),<d>定義同上。此項相當于全部點之間的“非鍵作用能U(ij)”之和,不再僅僅是相鄰點之間才有限制勢。任何點之間靠近都會造成能量升高,可以避免Elber-Karplus方法中出現的在能量極小點處結構點聚集、路徑自身交錯的問題,能夠使路徑充分地展開,確保過渡態區域有充足的采樣點。式中ρ和λ都是可調參數來設定權重。此外相對與Elber-Karplus方法還考慮了笛卡兒坐標下投影掉整體運動的問題。6.5 LUP方法(Locally Updated planes)
特點是優化過程中,只允許每個結構點R(i)在垂直于R(i-1)R(i+1)向量的超平面上運動。由于每步優化后R(i-1)與R(i+1)連線方向也會變化,故每隔一定步數重新計算這些向量,重新確定每個點允許移動的超平面。但是LUP缺點是結構點之間沒有以上述彈簧勢函數相連來保持間隔,容易造成結構點在路徑上分布不均勻,甚至不連續,還可能逐漸收斂至兩端的極小點。6.6 NEB方法(Nudged Elastic Band)
NEB方法集合了LUP與PEB方法的優點,其函數形式基于PEB。從PEB方法的討論可以看出,彈簧勢是必須的,它平行于路徑切線(R(i)-R(i-1)與R(i+1)-R(i)矢量和的方向)的分量保證結構點均勻分布在MEP上來描述它;但其垂直于路徑的分量造成的弊端也很明顯,它改變了這個方向的實際的勢能面,優化后得到的MEP'就與真實的MEP發生了偏差,造成corner-cutting問題。解決這個問題很簡單,在NEB中稱為nudge過程,即每個點在平行于路徑切線上的受力只等于彈簧力在這個方向分量,每個點在垂直于路徑切線方向的受力只等于勢能力在此方向上分量。這樣彈簧力垂直于路徑的分量就被投影掉了,而有用的平行于路徑的分量完全保留;勢能力在路徑方向上的分量也不會再對結構點分布的均勻性產生影響,被保留的它在垂直于路徑上的分量將會引導結構點地正確移動。這樣優化收斂后結構點就能正確描述真實的MEP,矛盾得到解決。彈簧力常數的設定也比較隨意,不會再對結果產生明顯影響。但是當平行于路徑方向能量變化較快,垂直方向回復力較小的情況,NEB得到的路徑容易出現曲折,收斂也較慢,解決這一問題可以引入開關函數,即某點與兩個相鄰點之間形成的夾角越小,此點就引入更多的彈簧勢垂直于路徑的分量,使路徑不易彎曲而變得光滑,但也會帶來一定corner-cutting問題。也可以通過將路徑切線定義為每個點指向能量更高的相鄰點的方向來解決。6.7 DNEB方法(Double Nudged Elastic Band)
彈簧勢垂直于路徑的分量壞處是造成corner-cutting問題,好處是避免路徑卷曲。更具體來說,前者是由于它平行于勢能梯度方向的那個分量造成的,若只將這個分量投影掉,就可避免corner-cutting問題,而其余分量的力F(DNEB)仍可以避免路徑卷曲,這便是DNEB的主要思想。故DNEB與NEB的不同點就是DNEB保留了彈簧勢垂直于路徑的分量其中的垂直于勢能梯度的分量。DNEB的這個設定卻導致結構點不能精確收斂到MEP上。正確的MEP上的點在垂直于路徑方向上受勢能力一定為0,但是當用了DNEB方法后,若其中某一點處路徑是彎曲的,即彈簧力在垂直于路徑方向上有分量F',而且此點勢能梯度方向不垂直于此點處路徑的切線,即F'不會被完全投影掉,F'力的分量F(DNEB)將繼續帶著這個點移動,也就是說結構點就不在正確的MEP上了。只有當結構點所處路徑恰為直線,即F'為0則不會有此問題。為了解決此問題有人將開關函數加入到DNEB,稱為swDNEB,當結果越接近收斂,即垂直于路徑的勢能力越小的時候,F(DNEB)也越小,以免它使結構點偏離正確MEP。一些研究表明DNEB和swDNEB相比NEB在收斂性(結構點受力最大值隨步數降低速度)方面并沒有明顯提升,DNEB難以收斂到較高精度以內,容易一直震蕩。
6.8 String方法
與NEB對力的投影定義一致,但點之間沒有彈簧勢連接,保持點的間距的方法是每步優化后使這些點在路徑上平均分布。6.9 Simplified String方法
String中計算每個點的切線并投影掉勢能力平行于路徑的分量的過程也去掉了,所有點之間用三次樣條插值來表述路徑,每一個點根據實際勢能力運動后,在路徑上重新均勻分布。優化方法最好結合RK4方法。NEB在點數較小的情況下比Simplified String方法能在更短時間內收斂到更高精度,但點數較多情況下則Simplified String更占優勢。6.10 尋找過渡態的chain-of-state方法
除非勢能面對稱且結構點數目為奇數,否則不會有結構點恰好落在過渡態。以能量最高的點作為過渡態只是近似的,為了更好地描述過渡態,可以增加結構點數,或者增加局部彈簧力常數,使過渡態附近點更密。根據已得到的點的能量,通過插值方法估算能量最高點是另一個辦法。近似的過渡態也可以作為QN法的初猜尋找準確的過渡態。
6.10.1 CI-NEB方法
NEB與String等方法都可以結合Climbing Image方法,它專門考慮到了定位過渡態問題。CI-NEB與NEB的關鍵區別是能量最高的點受力的定義,在CI-NEB中這個點不會受到相鄰點的彈簧力,避免位置被拉離過渡態,而且將此點平行于路徑方向的勢能力分量的符號反轉,促使此點沿著路徑往能量升高的方向上爬到過渡態。這個方法只需要很少的點,比如包含初、末態總共5個甚至3個點就能準確定位過渡態,是最有效率的尋找過渡態的方法之一。如果還需要精確描述MEP,可以在此過渡態上使用Stepwise descent方法、最陡下降法、RK4等方法沿勢能面下坡走出MEP,整個過程比直接使用很多點的NEB方法能在更短時間內得到更準確的MEP。6.10.2 ANEBA方法(adaptive nudged elastic band approach)
這個方法也是基于NEB,專用來快速尋找過渡態。一般想得到高精度的過渡態區域,NEB的鏈子上必須包含很多點,耗費計算時間。而ANEBA方法中鏈子兩端的位置不是固定的,而是不斷地將它們移動到離過渡態更近的位置,僅用很少幾個點的鏈子就可以達到同樣的精度。具體來說,設鏈子兩端的點分別叫A點和B點(對于第一步就是反應物和產物位置),先照常做NEB,收斂至一定精度后(不需要精度太高),改變A和B的位置為鏈子中能量最高點相鄰的兩個點,然后再優化并收斂至一定精度,再如此改變A和B的位置,反復經歷這一步驟,最終鏈子上能量最高點就是精確的過渡態。ANEBA相當于不斷增加原先NEB鏈子的過渡態附近的點數,但實際上點數沒有變。有研究表明ANEBA比CI-NEB效率更高,如果結合ANEBA與CI(稱CI-ANEBA),即先用ANEBA方法經上述步驟移動幾次A、B點,使之聚焦到過渡態附近,再用CI-NEB方法,效率可以進一步提高。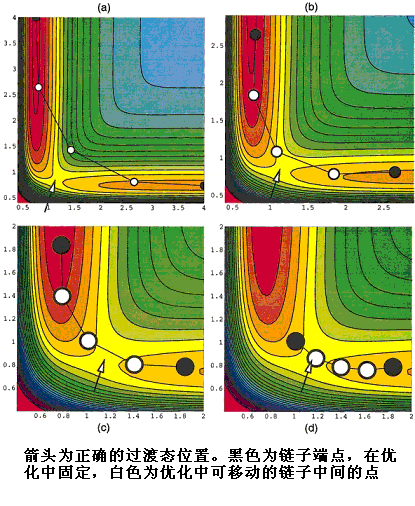
[圖16]ANEBA方法示意圖
6.11 chain-of-states方法的一些特點
NEB方法的設定只是決定了每一步結構點實際感受到的勢能面是怎么構成的,并沒有指定優化方法。NEB可以結合一些常見的優化方法,比如最陡下降法、共軛梯度法、quick-min、FIRE、L-BFGS法等(沒有線搜索步的全局L-BFGS法效率一般最高),但只能像前述尋找IRC方法一樣得到一條路徑。實際上很多情況反應的路徑不止一條,尤其是勢能面復雜的大分子構象轉變過程。當NEB結合構象搜索方法,比如分子動力學、蒙特卡羅等方法時,就可以用于尋找多條反應路徑。例如有幾條反應路徑,彼此間都有一定高度的勢壘分隔,如果初始給出的路徑在第i條附近,優化后只能收斂到第i條路徑,若對每個點使用分子動力學方法,設定一定溫度,則這些點有機會憑借動能越過勢壘到達另外一條路徑k附近,隨后逐漸降溫減小動能,相當于對它們進行最陡下降法優化,就找到了第k條路徑,若如此反復多次,有可能找到更多路徑。這類chain-of-states方法的優點還在于易于實現,算法簡單,只有能量和其一階導數是必須要算的,隨著體系尺度增大計算量的增加遠比基于Hessian矩陣的方法要小。對于大體系儲存Hessian并求逆亦是困難的,在某些情況下Hessian矩陣受計算能力制約只能在低水平方法下得到或者無法獲得,chain-of-states方法避免了這個問題,很適合用于分子力學研究生物大分子的結構變化路徑以及平面波基組下的DFT方法研究固體表面化學反應。此方法也容易并行化,例如可以每個節點負責優化其中一個或幾個點,只有計算彈簧力時才需要從另外節點傳入相鄰結構點坐標,數據通信量小,并行效率高。
6.12 高斯中opt關鍵字的path=M方法
與chain-of-states方法有一定類似之處,可以在一次計算中獲得優化后的過渡態、產物、反應物以及用于描述IRC的中間點結構,總共M個點。此方法須結合QST2或QST3關鍵字。結合QST2時,除反應物和產物以外剩下的M-2個點在二者冗余內坐標下線性插值產生,結合QST3則是剩下的M-3個點在反應物與過渡態、過渡態與產物之間插值產生。之后迭代的每一步主要分為以下幾個步驟:(1)初始輸入的反應物、產物通過RFO法向最優構型優化。(2)能量最高的點q(k)(此點在第一步確定)通過EF法向過渡態優化,并設一段圓弧通過q(k-1)、q(k)、q(k+1),此圓弧在q(i)處的切線作為EF方法選擇所跟蹤的本征向量的引導,類似于STQN步。(3)其余的點執行微迭代步驟(迭代內的迭代),其中包含類似于GS法的球面優化步驟以及調整間距步驟。可參考圖14,優化其中任意點q(i)前,首先獲得經過q(i-1)、q(i)并與q(i-1)的梯度相切的圓弧或曲線,將其在q(i)處的切線定義為T(i),然后定義一個在q(i)處法線與T(i)平行、經過q(i-1)與q(i)的球面,使q(i)限制在此球面上優化。然后在這些點依次相連的路徑上調整這些點的間距至平均,之后重復微迭代直至每一步力和位移都已收斂,或者有任何點位移超過了置信半徑。(4)檢查力和位移是否都已收斂至標準。這個方法看上去比單獨優化反應物、產物、過渡態并計算IRC省時間,但是實際用起來并不好用,容易出錯。6.13 CPK方法(Conjugate Peak Refinement)
在某種意義上稱為動態的chain-of-states方法。每條鏈子只含一個可動點,鏈子數由最初的一條開始不斷增加,對MEP的描述也越來越精確。CPK中的第一步類似LST,在連接反應物和產物的直線中找到能量最高點(稱為Peak),然后沿著共軛方向優化得到中間點,對中間點與反應物、中間點與產物分別再做上述步驟,先找到最大點再共軛優化,如此反復直到收斂。最后將反應物、產物以及執行CPK過程中所有優化后的點相連,就得到了近似的反應路徑。CPK方法所得的反應路徑可以經過很多過渡態,很適合尋找一些涉及到復雜結構重排、包含甚至上百個過渡態的構象變化路徑,如蛋白質局部折疊/去折疊過程。CPK方法缺點是實現起來相對復雜,定位過渡態較為費時。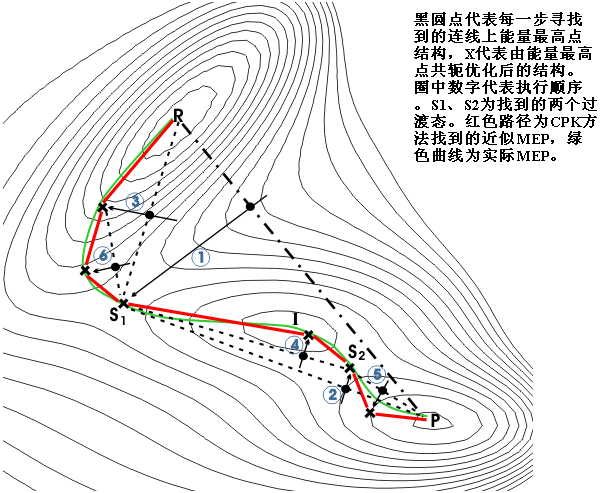
[圖17]CPK方法示意圖