Gaussian中分析振動模式成份的關鍵詞freq=intmodes
Gaussian中分析振動模式成份的關鍵詞freq=intmodes
文/Sobereva @北京科音 2011-Oct-27
在Gaussian中,在freq關鍵詞中有一個對分析振動模式很有用的選項intmodes,可惜在手冊中對它的描述十分晦澀,導致很多人沒注意到它。這里簡單介紹一下。
freq=intmodes可以把每個簡正振動模式分解為各個冗余內坐標的貢獻。這可以將振動模式的討論定量化,也可以幫助指認振動模式的特征。這里以HF/6-31G*下的乙醇為例說明。下面的動畫是乙醇的第二個振動模式
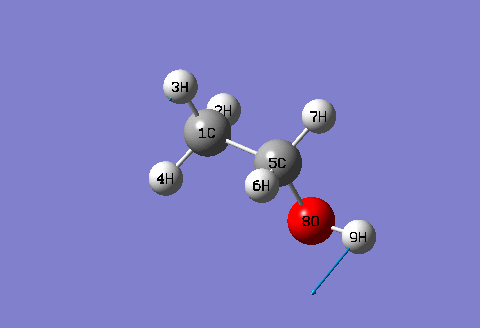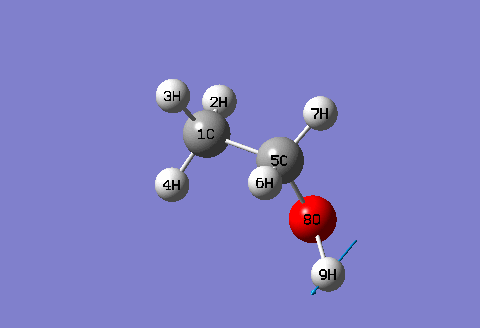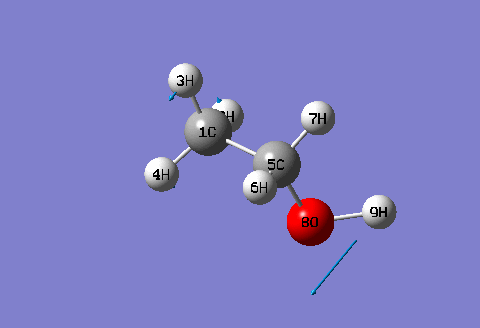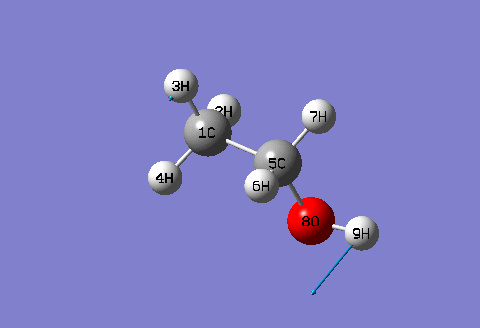
用了freq=intmodes后,在熱力學數據輸出的后面,可以找到這個振動模式中各個冗余內坐標所占成份
----------------------------
! Normal Mode 2 !
-------------------------- --------------------------
! Name Definition Value Relative Weight (%) !
--------------------------------------------------------------------------------
! D1 D(2,1,5,6) -0.0977 3.5 !
! D2 D(2,1,5,7) -0.0977 3.5 !
! D3 D(2,1,5,8) -0.1078 3.9 !
! D4 D(3,1,5,6) -0.1015 3.7 !
! D5 D(3,1,5,7) -0.1015 3.7 !
! D6 D(3,1,5,8) -0.1116 4.0 !
! D7 D(4,1,5,6) -0.0977 3.5 !
! D8 D(4,1,5,7) -0.0977 3.5 !
! D9 D(4,1,5,8) -0.1078 3.9 !
! D10 D(1,5,8,9) 0.6058 21.9 !
! D11 D(6,5,8,9) 0.5882 21.3 !
! D12 D(7,5,8,9) 0.5882 21.3 !
--------------------------------------------------------------------------------
可見,三個二面角D(1,5,8,9)、D(6,5,8,9)和D(7,5,8,9)所占成分很大,總共占了約65%。與動畫對照,確實這個數值是比較合理的。D1至D9這些二面角都是對應甲基扭轉,總共占約33%。因此,在描述這個振動模式時可以寫 33% τ(C-C), 65% τ(C-O),這里τ符號通常用來表示扭轉項。
通過查看冗余內坐標的貢獻,不需要通過觀看動畫,也能很容易地想象出振動方式,例如乙醇的第19個模式
----------------------------
! Normal Mode 19 !
-------------------------- --------------------------
! Name Definition Value Relative Weight (%) !
--------------------------------------------------------------------------------
! R1 R(1,2) -0.5164 20.6 !
! R2 R(1,3) 0.8206 32.8 !
! R3 R(1,4) -0.5164 20.6 !
! R5 R(5,6) 0.056 2.2 !
! R6 R(5,7) 0.056 2.2 !
! A2 A(2,1,4) 0.0474 1.9 !
! A5 A(3,1,5) -0.0474 1.9 !
! D1 D(2,1,5,6) -0.0358 1.4 !
! D2 D(2,1,5,7) -0.0508 2.0 !
! D3 D(2,1,5,8) -0.0433 1.7 !
! D7 D(4,1,5,6) 0.0508 2.0 !
! D8 D(4,1,5,7) 0.0358 1.4 !
! D9 D(4,1,5,8) 0.0433 1.7 !
--------------------------------------------------------------------------------
占成分最大的三個內坐標都是C-H bond項(共占74%),其中R2的Value是正值,R1和R3是負值,即相位相反。因此,這個振動模式主要特征是甲基的不對稱伸縮振動。
使用freq=intmodes的時候可以自定義冗余內坐標,給研究振動模式的成份帶來很大的靈活性。例如,在乙醇第二個振動模式的動畫中,可以看到7號和9號原子之間的距離在振動過程中會有很大變化。于是,可以嘗試給7號和9號原子間增加一個冗余內坐標,來了解它對此振動模式的貢獻。方法是寫上freq=(modredundant,intmodes),然后在分子坐標后面空一行寫B 7 9。此時輸出的結果為
----------------------------
! Normal Mode 2 !
-------------------------- --------------------------
! Name Definition Value Relative Weight (%) !
--------------------------------------------------------------------------------
! R8 R(7,9) 0.379 12.0 !
! D1 D(2,1,5,6) -0.0977 3.1 !
! D2 D(2,1,5,7) -0.0977 3.1 !
! D3 D(2,1,5,8) -0.1078 3.4 !
! D4 D(3,1,5,6) -0.1016 3.2 !
! D5 D(3,1,5,7) -0.1016 3.2 !
! D6 D(3,1,5,8) -0.1116 3.5 !
! D7 D(4,1,5,6) -0.0977 3.1 !
! D8 D(4,1,5,7) -0.0977 3.1 !
! D9 D(4,1,5,8) -0.1078 3.4 !
! D10 D(1,5,8,9) 0.6057 19.3 !
! D11 D(6,5,8,9) 0.5882 18.7 !
! D12 D(7,5,8,9) 0.5882 18.7 !
--------------------------------------------------------------------------------
新增加的冗余內坐標R8所占成份確實不小,達到12%。由于它描述了部分原本被D10、D11和D12所描述的振動特征,故D10、D11和D12所占成分相比在新增R8之前有所下降。
曾經寡人寫過一個用GAR2PED讀取Gaussian輸出文件做PED分析的帖子,可以將簡正振動模式分解成各個基團特征振動模式的貢獻,見http://www.shanxitv.org/75,其中也介紹了振動模式分解方法的基本原理。雖然freq=intmode和GAR2PED都是用來將振動模式分解,但二者還是有差別的。freq=intmode是以冗余內坐標為基,而GAR2PED是以常見有機基團的特征振動模式為基。它們各有長處。來看乙醇第四種振動模式。freq=intmodes的輸出為
----------------------------
! Normal Mode 4 !
-------------------------- --------------------------
! Name Definition Value Relative Weight (%) !
--------------------------------------------------------------------------------
! A1 A(2,1,3) -0.044 1.5 !
! A3 A(2,1,5) -0.2291 7.6 !
! A4 A(3,1,4) 0.044 1.5 !
! A6 A(4,1,5) 0.2291 7.6 !
! A7 A(1,5,6) 0.2159 7.1 !
! A8 A(1,5,7) -0.2159 7.1 !
! A11 A(6,5,8) 0.0463 1.5 !
! A12 A(7,5,8) -0.0463 1.5 !
! D1 D(2,1,5,6) -0.2361 7.8 !
! D2 D(2,1,5,7) -0.2361 7.8 !
! D3 D(2,1,5,8) -0.0506 1.7 !
! D6 D(3,1,5,8) 0.1539 5.1 !
! D7 D(4,1,5,6) -0.2361 7.8 !
! D8 D(4,1,5,7) -0.2361 7.8 !
! D9 D(4,1,5,8) -0.0506 1.7 !
! D11 D(6,5,8,9) 0.3223 10.7 !
! D12 D(7,5,8,9) 0.3223 10.7 !
--------------------------------------------------------------------------------
與前面給出的兩個振動模式不同,明顯參與這個振動模式的冗余內坐標較多,所以列出了一大串。其中貢獻值最大的冗余內坐標也并沒有顯出很大的優勢,分析上有些不便。若想定量分析,需要尋找冗余內坐標與基團特征振動之間的關系,然后再做加和處理。而GAR2PED輸出的結果則很清楚:
4. 886.86 0.25 16( 40.) -12( 33.) 18( 13.) -13( 11.)
在操作中,已經定義了12、13號基團特征振動屬于甲基變形振動,而16、18號為亞甲基變形振動。因此,從GAR2PED的結果很明顯看出這個振動模式對應甲基和亞甲基強烈耦合的變形振動。顯而易見,對于涉及冗余內坐標過多的簡正振動,用GAR2PED比起用freq=intmodes往往更容易考察振動特征。
而GAR2PED相對于freq=intmodes也有很多不足。首先GAR2PED是獨立的程序,沒關鍵詞用起來方便。而且,GAR2PED在操作界面上設計得挺別扭,指定基團過程麻煩,還需要“摸黑”操作。另外程序也沒有說明書或教程。更關鍵的是,GAR2PED主要面向化學鍵典型的普通有機分子,內置的基團類型是很有限的,對于很多分子都沒法用內置的基團指定完全,而freq=intmodes則是完全普適的。所以,不妨結合使用二者,揚長避短。