Potential energy distribution(PED)計算軟件GAR2PED使用簡介

PED簡介：

每種特征基團都有其特有的振動方式，比如甲基有對稱伸縮、搖擺、對稱彎曲等，這些基團的振動模式一般在不同分子中都有保守性。然而，它們在分子中并非孤立的，會與分子環境發生耦合，各種振動模式相互混合導致原有振動頻率和振動模式都發生變化。基團特征振動模式不會明顯受與之距離較遠原子的影響，與基團相連的原子若與基團內原子質量差異大或振動模式力常數差異大，基團振動模式仍然保持較好獨立性。然而，當與基團相連的原子質量相近且振動模式力常數亦相近，振動的耦合就相當明顯，這種情況下分析分子簡正振動模式往往有很大困難，從復雜的振動向量上無法直接指認出振動模式的歸屬、究竟屬于哪個基團、哪類振動。PED(Potential energy distribution)是將簡正振動模式分解的分析方法，可以獲得每種基團特征振動模式產生的貢獻，比較它們的百分比可以容易地了解簡正振動模式的本質特點，由哪種特征振動模式所主導。基本原理如下：

存在這樣的關系：Λ=L^(T)FL。其中F是力常數矩陣，L是F的本征向量矩陣，它的第N列就是第N個簡正振動向量。L^(T)是L的轉置。Λ是對角矩陣diag(λ1,λ2...)。即是說，將內坐標變換為簡正振動坐標Q后，力常數矩陣成為對角矩陣，其元素λ_N就是簡正振動模式N的力常數。根據諧振勢模型，V(Q_N)=0.5*Q_N^2*λ_N。將λ_N明確寫成分量加和形式，即
λ_N=Λ(N,N)=∑[i]∑[j]L^(T)(N,i)F(i,j)L(j,N)=∑[i]∑[j]F(i,j)L(j,N)L(i,N)
其中，只有i=j的貢獻才是最主要的。因此，通過比較每個內坐標i的力常數對λ_N的貢獻量F(i,i)L(i,N)^2就可以了解哪個內坐標對第N種簡正振動模式有主要貢獻，一般通過百分比來表達，即η(i,N)=F(i,i)L(i,N)^2/(∑[j]F(j,j)L(j,N)^2)*100%。若不用內坐標，而改成以基團特征振動向量作為基，得到的就是各個基團各種特征振動模式對簡正振動模式的貢獻百分比。

做PED分析軟件有不少，如VEDA、MOLVIB、BIOVIBAN、VIBRATZ、RAMVIB、nmodes、FCART01等。這里介紹的GAR2PED可以免費獲得，下載地址：http://www.ccl.net/cca/software/SOURCES/FORTRAN/gar2ped/gar2ped.tar.Z

GAR2PED是讀取Gaussian的Freq任務的archive信息（即末尾輸出的很緊湊的那部分）來計算PED等信息的工具。由Martin和Alsenoy于1995年開發，最重元素支持到Br。程序最初給Gaussian94用，由于現在的Gaussian功能已經擴充了，以及有了Gview，GAR2PED輸出的很多信息已經意義不大，這個程序目前的用處主要就是計算PED了。程序可以兼容最新的Gaussian09。

編譯：

GAR2PED用Linux下的一些編譯器不好編譯。用CVF6.5編譯則很簡單，把所有.f文件（除了pullarc.f）加入工程里然后編譯，結果命名為gar2ped.exe。再把工程清空，將pullarc.f放進工程里，編譯結果命名為pullarc.exe。

注意！如果用于Windows版Gaussian結果分析，要把pullarc的line29的1\\1\\改為1|1|。因為Windows版Gaussian的archive部分每項使用|分隔而不是\來分隔。

我用CVF6.5編譯好的Windows版（pullarc.exe編譯前已改為1|1|），下載地址：/usr/uploads/file/20150609/20150609192457_70016.rar。

運行方法（對于我編譯的版本而言）

對于Windows版Gaussian：將Gaussian的Freq任務（無需#P。另外不要把opt和freq任務和在一起執行）的運行結果命名為比如叫test.log，放在pullarc.exe所在目錄下，運行pullarc test。pullarc程序會讀取test.log，如果屏幕上正確顯示出archive信息的第一行，就輸入y，將得到test.xyz（分子結構的笛卡爾坐標）和test.arch。然后把test.arch里面的|全都替換成\。

對于Linux版Gaussian：同上，但是先把輸出文件的archive部分的開頭1\1\改成1|1|，然后執行pullarc test，就能得到test.xyz和test.arch。之后把test.arch中的開頭的1|1|改回1\1\，

（實際上，pullarc的目的就是把archive部分提取出來，并截掉開頭的空格。如果是在笛卡爾坐標下計算的，pullarc的工作完全可以手動完成，用Ultraedit很方便；但如果是在內坐標下計算的，就必須用pullarc處理，因為它生成的test.xyz將會被gar2ped讀取。）

之后運行gar2ped test，就會讀入test.arch并計算一些信息。如果想算PED，在問skip internal part的時候輸入n進入設定PED的界面（見后文）。

輸出的test.out是GAR2PED運行結果，如果做了PED則包括PED信息。另外輸出的一堆test.nomo.N.xyz是指第N個簡正振動模式動畫每一幀坐標，用VMD打開就可以觀看動畫。test.nomos.xyz是所有簡正振動模式向量。test.xyznew是根據當前力常數矩陣按牛頓法優化的下一步分子結構。test.apt.xyz是GAPT電荷。這些信息除了PED外其實基本上在Gaussian的輸出文件里都有，也基本都一致。

設定和計算PED：

進入設定PED的界面后要依次定義3N-6或3N-5（線性）個坐標，每個簡正振動模式將分解為這些坐標的貢獻。注意不要輸入錯，否則要全部重來。隨時按-1可以看到還剩幾個坐標沒有定義。

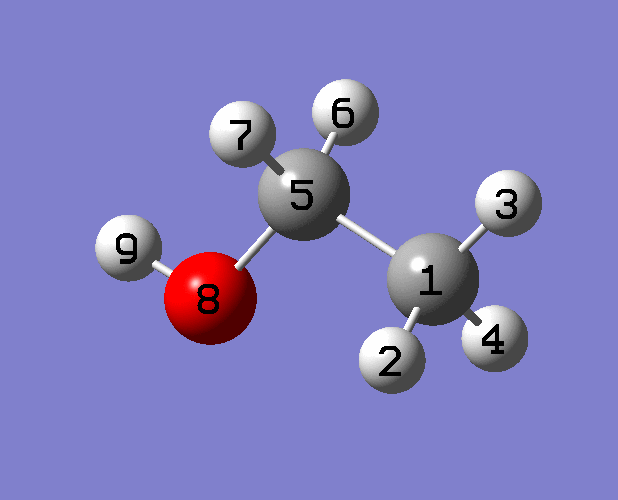
這里的示例分子是HF/6-31G* freq得到的乙醇，需要設定21個坐標：
(1) 按1，加入了所有8個鍵伸縮項。
(2) 按3，并輸入1,2,3,4,5（原子序號），加入了5個甲基特征變形運動模式，它們是由甲基中鍵角振動耦合而成的。注意這不包括甲基鍵伸縮模式，這在剛才按1的時候已經添加了。
(3) 按4，并輸入5,1,8,6,7，加入了5個sp3亞甲基變形運動模式。
(4) 按13，并輸入5,9,8，加入C-O-H彎曲振動模式。
(5) 按2，并輸入1,5，加入甲基-亞甲基的扭轉項。注意輸入扭轉項時是指輸入A-B-C-D當中B、C兩個原子序號，而不是A、D的。
(6) 按2，并輸入5,8，加入羥基-亞甲基的扭轉項。
此時輸入-1，得知21個振動坐標都設好了，輸入0退出。

將基本振動模式輸入順序匯總以便接下來對照：
1~8 stretch
9~13 -CH3 deformation vibriation
14~18 X-CH2-Y deformation vibration
19 X-O-H bend
20 CH3-CH2- torsion
21 HO-CH2- torsion

輸出結果如下
     POTENTIAL ENERGY DISTRIBUTION

               FREQ      INTENS          CONTRIBUTIONS .. COORD(%;>5%)

       1.      270.30     27.82      20( 82.)  21( 14.)
       2.      317.09    126.55      21( 89.) -20(  8.)
       3.      447.79     12.22      15( 78.) -13( 11.)
       4.      886.86      0.25      16( 40.) -12( 33.)  18( 13.) -13( 11.)
       5.      978.16      6.25       4( 43.)   7( 24.)  13( 19.) -12(  7.)
       6.     1133.06     59.55       4( 33.) -13( 21.)  19( 19.)  -7( 11.)  12(
  7.)
       7.     1217.27     26.23       7( 65.) -13( 11.)  -4(  6.)  19(  6.)
       8.     1298.71      7.13      16( 56.)  12( 22.) -18( 10.)  13(  7.)
       9.     1395.55    121.66      19( 57.) -17( 14.)  -7(  9.)  13(  8.)  15(
  5.)
      10.     1423.79      0.10      18( 86.)  12(  9.)
      11.     1549.79      0.12       9( 81.)  17( 14.)
      12.     1613.59     17.15      17( 54.)  -9( 12.)  -4( 12.)  19( 11.)  11(
  7.)
      13.     1628.88      2.87      10( 69.)  11( 23.) -12(  6.)
      14.     1645.91      3.05      11( 58.) -10( 19.) -17(  6.)  14(  6.)
      15.     1686.01      3.67      14( 90.)
      16.     3175.48     78.26       5( 49.)   6( 49.)
      17.     3200.29     82.58       6( 48.)  -5( 48.)
      18.     3211.82     20.60       2( 43.)   3( 28.)   1( 28.)
      19.     3276.06     48.90       2( 55.)  -1( 22.)  -3( 22.)
      20.     3288.53     53.85       3( 49.)  -1( 49.)
      21.     4114.50     41.15       8(100.)

根據振動模式的主要成分可以指認它的特征。這個表顯示了每種簡正振動模式由哪些剛才設定的特征振動模式所組成，特征振動模式編號順序就是剛才輸入時的順序，其中只有貢獻大于5%的才會被輸出。建議同時對照Gview的振動模式的動畫來考察，以檢驗結果合理性。

例如前兩個簡正振動模式分別對應CH3-CH2-（第20號）和HO-CH2-（第21號）基團扭轉，因為它們的成分占主導地位，同時它們之間也有一定耦合。

第三個當中第15個特征振動模式占78%，查看之前匯總列表得知它主要屬于亞甲基變形振動，再從振動模式動畫上看，得知它是X-CH2-Y角變形運動。

第四個當中，第16和第12號特征振動模式分別占40%和33%，說明這是甲基和亞甲基變形運動強烈耦合的振動模式。12的前面是負號，說明這兩種基本振動模式相位在簡正振動模式中是相逆的。

第五個當中，鍵伸縮振動占了43%+24%=67%，還摻入少量甲基變形運動。通過振動模式動畫得知這是亞甲基相連重原子的對稱伸縮。

其它振動模式的分析依此類推，不再累述。簡正振動模式編號從16開始進入了3000cm-1區域，都是氫伸縮振動了，例如第20個簡正振動模式當中，1號和3號特征振動模式都貢獻49%，但相位相反，說明是甲基或亞甲基的氫不對稱伸縮，從動畫上看是甲基的不對稱伸縮。