淺談PCA與g_covar+g_anaeig+ddtdp+sigmaplot做自由能面圖的方法
淺談PCA與g_covar+g_anaeig+ddtpd+sigmaplot做自由能面圖的方法
文/Sobereva @北京科音 2010-Nov-11
其實這個問題兩年前就寫過帖子討論過,但由于近來又有人問,也覺得在作圖的時候有些問題值得補充說明一下,故撰此貼。
1 PCA淺談
N個原子的柔性大體系運動軌跡需要3N維笛卡爾坐標描述,然而這樣高維度的數據很難直觀分析,尤其是隨著計算能力越來越高,模擬的體系也越來越大、模擬的時間越來越長、內容越來越復雜,這就需要發展更多的分析方法去挖掘出海量信息中感興趣的信息,而使數據“噪音”被過濾,比如從復雜軌跡中了解蛋白的折疊/去折疊主要路徑、酶重要域的大尺度運動行為、體系構象分布傾向、配體/殘基突變/質子化等效應對體系構象的影響等等。一種解決途徑是將坐標維度約化得盡可能低,同時盡可能使原始高維空間下的信息最大程度保留,這樣就方便人直觀考察體系的運動過程。統計學上的Principal component analysis(PCA)正適合解決這個問題,一般是將變量選為3N個笛卡爾坐標(也有其它選擇方式,諸如二面角PCA等),要處理的數據集就是各幀結構。首先由MD軌跡構建協方差矩陣,然后計算其本征值和本征向量。這3N個本征向量也就是由原始笛卡爾坐標組合而成的新坐標,它們彼此間從協方差的意義上說是不相關的(也就是把軌跡轉換到這些新坐標上后,協方差均為0)。本征向量對應的本征值越大說明體系的運動行為越多地體現在這個本征向量坐標上,若最大的幾個本征值的和除以協方差矩陣的跡等于0.85,說明在這幾個維度上就可以描述體系85%的運動信息。這樣有高本征值的本征向量也稱主成分(Principal component, PC)。
實際上一般不將大分子全部N個原子都考慮,比如研究蛋白骨架行為就考慮alpha-C即可,研究某一個區域的運動就選擇這個區域的原子即可,不僅計算會省時、省內存,而且如果把過多無關原子也考慮進去,若它們在模擬中運動也比較明顯,則感興趣的原子的運動反倒被掩蓋了。另外,做PCA前必須將整個軌跡向指定幀的結構做align以消除平動和轉動的影響,前文所謂“運動”皆是指體系的內運動,否則分子內運動行為會被整體運動掩蓋住。(實際上即便做了align,整體運動的成分也并沒徹底消除,因而出現了基于內坐標的PCA方法,即dihedral PCA)。限于本文篇幅和目的不再對PCA進行更具體討論,可以參考Principal Components Analysis: A Review of its Application on Molecular Dynamics Data。下載地址:/usr/uploads/file/20150610/20150610200236_48141.pdf
2 自由能面圖(Free energy landscape)
一般所謂自由能面圖就是通過一張圖來描述大分子各種構象自由能的大小。這就需要知道各種構象{x}出現的概率密度P(x),然后通過Boltzmann關系計算G(x):
G(x)=-kT*Ln(P(x))+常數
常數項不用管,它和配分函數有關,是極難計算的。我們關心的只是各種構象的相對自由能而不是絕對自由能,常數項與此無關,所以做自由能面圖時常數項可以取任意值。
在平面上最能清晰展現出來的是二維坐標的圖,通常將自由能面圖的兩個坐標軸分別取為PC1、PC2(最大兩個本征向量),若選取的原子在模擬中運動范圍大,它們一般已經能描述體系70%以上的運動行為。如果PC3的本征值也不小,可以再加一張圖以PC1和PC3為軸。(對某些問題也可以用其它描述體系特征的量為軸,比如轉動半徑)
選定了坐標軸后需要將原始軌跡根據相應的本征向量投影到這兩個坐標軸上。如果做散點圖,圖上就會顯現疏密不均的小點,點越密集處說明構象出現概率越大,相應的構象自由能越低。接下來將圖上的散點分布轉換成概率分布P(x),再由前式獲得G(x),做它的等值線圖或者填色圖就得到了自由能面圖。接下來將給出實例,通過gromacs的g_covar和g_anaeig子程序、筆者開發的ddtpd以及sigmaplot繪圖程序繪制一個10ns模擬中酶蛋白骨架的自由能面圖。
3 使用g_covar
g_covar用來生成軌跡的協方差矩陣并計算本征向量和本征值。運行方法(方括號代表可選的項):
g_covar -f 輸入的軌跡文件 -s 輸入的結構文件 -n [輸入的index文件] -o 輸出的本征值文件 -v 輸出的本征向量文件 -av 輸出的平均結構文件 -l 輸出的日志文件 -ascii [輸出的協方差矩陣數據文件] -xpm [圖形描述的N階協方差矩陣] -xpma [圖形描述的3N階協方差矩陣]
例如g_covar -s a-sol-prnowat.gro -f allnowat.xtc -o eigenvalues.xvg -v eigenvectors.trr -xpma covapic.xpm
其中allnowat.xtc是一個10000幀的10ns的軌跡,a-sol-prnowat.gro是與它對應的某一幀結構文件。運行后程序會問將哪些范圍原子做align,選C-alpha,說明每幀的C-alpha將會朝著輸入的結構文件做align;然后會問對哪些范圍原子做PCA,選C-alpha(也可以與剛才選的不同)。
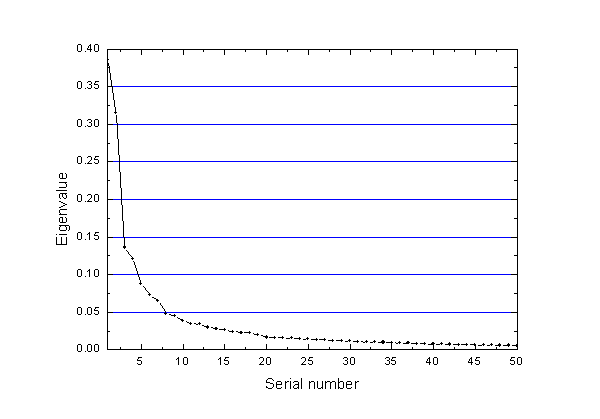
由于alpha-C共有232個,所以協方差矩陣是3*232=696階的方陣,故eigenvalues.xvg含有696個值,本征值順序是從大到小。由于這個體系處于平衡態,骨架整體運動不明顯,所以由eigenvalues.xvg信息繪制的下面的“本征值大小vs本征值序號”的圖上看,雖然隨序號增大本征值立刻降低,但是收斂不快,超過5號后降低平緩,前十個本征向量總共只能解釋體系58.7%的運動信息,PC1和PC2一起只能解釋32.2%的信息,說明對此體系全部alpha-C原子做PCA意義不大。由于本文目的主要是說明如何做自由能面圖,所以這無所謂。
696個本征向量分別記錄在eigenvectors.trr中的每一幀中,其原子坐標代表原3N個笛卡爾坐標是如何組合成本征向量的,這個軌跡雖然也可以用可視化軟件觀看,但沒什么意義。實際上得到的軌跡有698幀,是因為第一幀保存的是align時的參考結構,第二幀是軌跡平均結構。
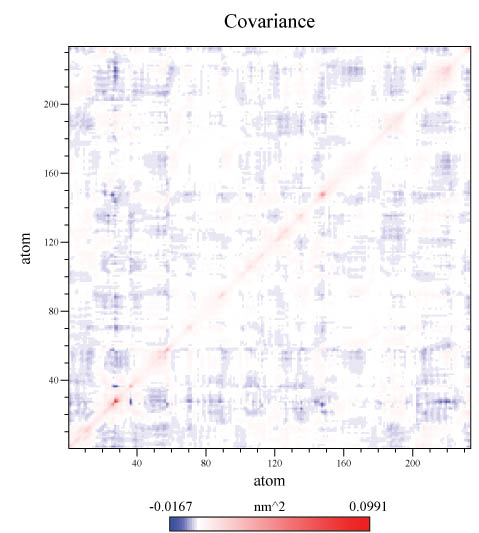
covapic.xpm是圖形化描述的協方差矩陣,在Linux下可以用比如GNOME之眼打開;若在windows下打開,可以先用gromacs自帶的xpm2ps轉換成eps文件,再用諸如再用諸如photoshop、GhostView查看(也可以用adobe distiller等軟件轉成pdf)。此文件中3N*3N協方差矩陣已經被轉化成N*N協方差矩陣,即坐標軸刻度對應原子序號。越紅的區域說明矩陣元數值大,白的區域對應矩陣元數值為0,越藍代表越負。矩陣對角線就是方差,必大于零,故是白色或偏紅色。圖中坐標為(28,28)的區域較紅,說明26~29號alpha-C在模擬中運動比較明顯,實際上這幾個殘基正處于蛋白質柔性末端,直接考察軌跡也能得出相同結論。非對角元區域可正可負,越正/越負說明相應兩個原子運動方式越趨于正相關/負相關。圖中雖有深藍色區域,但從色彩刻度上看其值其實并不很負。alpha-C原子間運動多呈負相關和殘基側鏈間靜電作用導致排斥/吸引而使相關原子產生反相運動有關。若是研究同一殘基的原子運動的協方差矩陣,由于某原子運動會拉動周圍原子同向運動,所以對角線附近也會偏紅。
4 使用g_anaeig
g_anaeig的主要功能之一是將軌跡投影到選取的本征向量上,這里要投影到PC1和PC2上,執行:
g_anaeig -f allnowat.xtc -s a-sol-prnowat.gro -v eigenvectors.trr -first 1 -last 2 -2d 2d.xvg
首先allnowat.xtc各幀會被align到eigenvectors.trr里記錄的參考結構上,然后投影到-first和-last所選的本征向量,命令中1、2就是指前兩個本征向量,即PC1和PC2。-2d 2d.xvg代表將每幀結構在PC1和PC2上的投影值輸出到2d.xvg。
如果裝了xmgrace,運行xmgr 2d.xvg,調整顯示方式得到下面的散點圖:
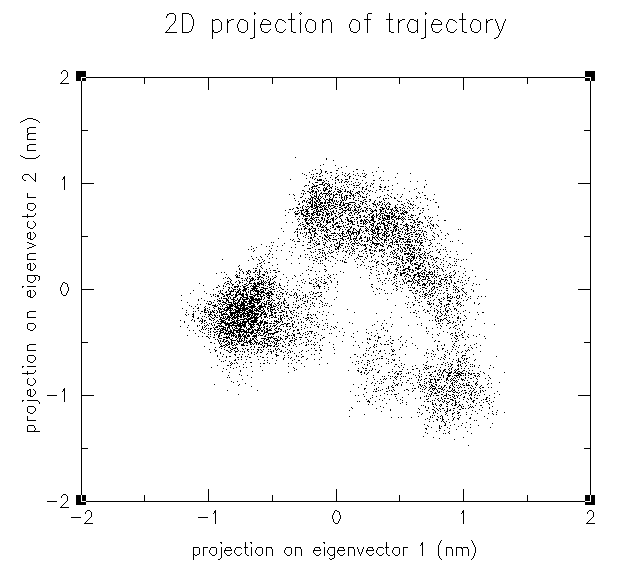
每個點代表一幀結構,越密集的區域說明這個區域對應的分子構象能量越低。在密集區域中隨便取一個點,若這個點的編號是i,就說明軌跡中第i幀的構象是較穩定、能量較低的,反之稀疏區域的點對應的幀是不穩定構象。在xmgrace中獲得點的編號首先要將感興趣的區域放大,然后在設定符號/圖例的頁面中將顯示的符號設為Index,數據點就以其編號顯示了。利用PCA可以做簇分析,比如圖中左側一團密集的點對應的構象就可以歸為同一個簇,即它們構象相似。下圖是投影到PC10和PC11的結果。
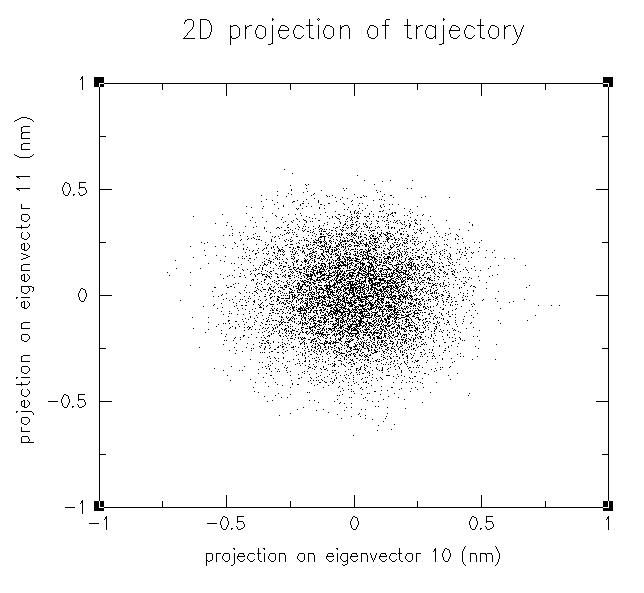
比較可見,投影到PC10、11后數據點都湊在一起成球狀,看不出任何特征,構象的差異引起的能量差異得不到充分顯現,也不可能做簇分析。這就是為什么軌跡要投影到PC1、2的原因,PC1、2最能描述體系運動模式,或者說PC1、2能將體系的自由能面形貌最大程度地展現,使其細節特征能夠充分地暴露出來。
使用g_anaeig時如果用“-3d 文件名”,會將軌跡投影到從-first到-last的3個主成分上,輸出的是.gro文件,原子坐標的X/Y/Z值分別代表在三個PC上的投影,原子編號就是幀號。如果用“-proj 文件名”,可以同時將軌跡投影到從-first到-last的任意多個主成分上。比如投影到前六個PC,用xmgr對得到的.xvg文件作圖得到:
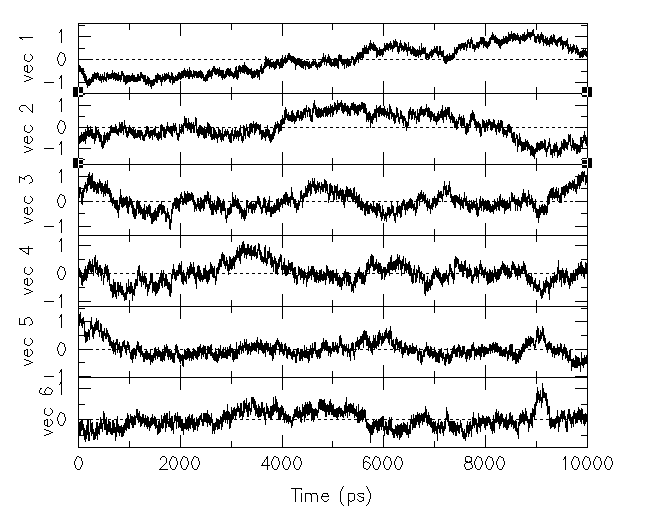
圖中表現軌跡在PC1至PC6上投影值隨時間的變化。前兩個PC波動比較大,說明其數據方差大,這也說明為何在協方差矩陣中其對應的本征值大(本征值=方差)。后面幾個PC的波動依次漸緩,尤其是PC5和PC6,完全就像是體系在平衡態的RMSD曲線,體系的運動信息用它們根本描述不出來。
5 使用ddtpd做自由能面圖
5.1 ddtpd簡介
ddtpd全稱Converting dot distribution to probability distribution,是筆者開發的將上述-2d關鍵詞生成的點分布.xvg文件轉換成概率或自由能分布的小程序。原理是根據數據最大、最小值設定空間范圍,然后根據用戶輸入的兩方向格點數將空間劃分為一個個微小的格子,根據 P(x,y)=此網格內數據點數量/總數據點數量/網格面積 來計算不同位置的概率密度,進而轉化為自由能。ddtpd v1.3還支持高斯展寬功能,用于解決數據點較少時圖像難看的問題。
ddtpd v1.3的下載地址:/usr/uploads/file/20151115/20151115220021_45515.rar。
壓縮包里的test.xvg就是下文要用的xvg文件。
5.2 作圖步驟
啟動ddtpd后,依次輸入
2d.xvg //文件名
100 //將X軸劃分的格子數
100 //將Y軸劃分的格子數
2 //選擇輸出方式。2代表輸出-LnP
y //令P=0的點也輸出。此時數據被輸出到當前目錄的result.txt下。由于沒有數據點分布的區域P=0,沒法求對數,對這樣的區域ddtpd認為其P是一個很小的常數,自由能直接設為-Ln0.000001。
y //把-LnP最負的值,此處為-0.821262設為自由能的零點。我們感興趣的只是相對值,所以可以加減任意常數,這樣所有值加上0.821262之后數據最小值就是0,設定色彩刻度會比較方便。此時數據將輸出到當前目錄的result2.txt下,前兩列是PC1和PC2的坐標,第三列是-LnP的值。
sigmaplot比較易用,適合做填色圖描繪自由能面。為了讓色彩刻度中色彩變化明顯的范圍覆蓋-LnP數據主要分布范圍,以使圖上數值大小不同的區域能夠被清晰地區分開,需要對ddtpd輸出的數據做一下調整。注意程序最后在屏幕上輸出“Now maximum result is 2.772589”(注:這個最大值是指除P=0以外區域的值)以及“14.636773 means P=0 in this minival area”。打開result2.txt,將P=0的值替換為最大值加上1.0~1.5得到的整數或半整數(湊整數/半整數只是為了方便而已),此例中就是將14.636773替換為4。由于數據較多,不同文本編輯器替換速度由于算法不同差異明顯,建議用Ultraedit。
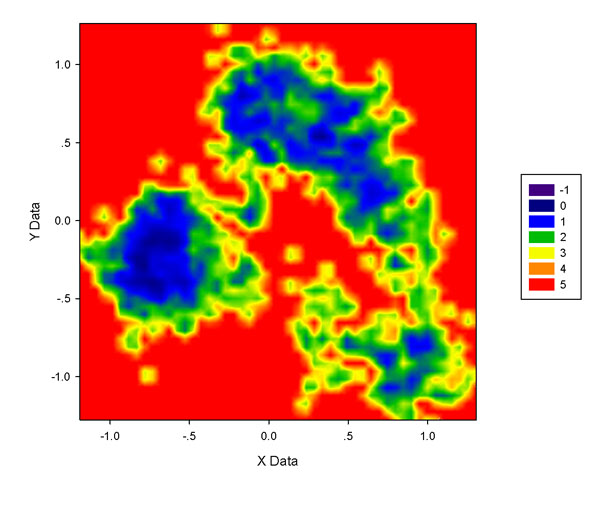
然后將result2.txt放到sigmaplot里做圖,得到下圖(色彩刻度為默認):
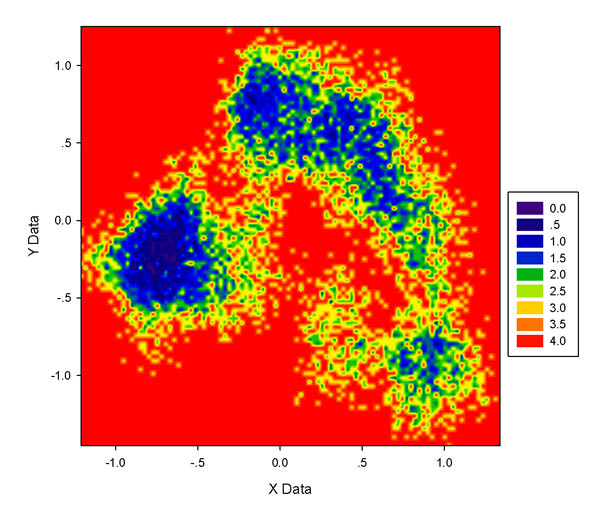
注意這類圖的單位是kT,k是Boltzmann常數(J/K),T是當前模擬時的溫度(K),所以kT=T*1.3806503*10^-23J。如果想轉化到kcal/mol,就除以4186再乘以阿伏伽德羅常數。比如對于圖中的4位置,假設模擬是在310K進行的,就是4*310*1.3806503*10^-23/4186*6.023*10^23=2.4633kcal/mol.
5.3 格點數目的選擇對圖像的影響
上圖整體效果不錯,越藍區域說明自由能越低,圖中顯示構象主要分布在左、右上和右下三部分,自由能依次升高。不過圖也略有缺點,也就是諸如右上角低能量區域有很多紅色或黃色的窟窿,藍色區域沒那么連貫,顯得細碎。這與格點數目選取有關,格點數太多不僅圖像細碎,做圖還慢;格點數太少雖然會連貫,但是缺乏細節,圖像邊緣時常呈現棱角。一般來說,.xvg文件中數據點越多可以用越多的格點,圖像邊緣細節會更豐富,且不使圖像細碎;當數據點不夠多的時候用較大數目格點只有壞處,得到的圖甚至就像散點圖。下圖是此xvg文件50*50格點和200*200格點的圖,后者凌亂很不好看,而前者又有些模糊,由于前面100*100做的圖也略有零碎,所以75*75格點比較適合做這個xvg文件的填色圖。對不同體系應當反復摸索最適合的格點設定,一般不超過60*60至120*120范圍。另外,調整色彩刻度上下限也能有效改善圖像效果,這里就不談了,請自行摸索。
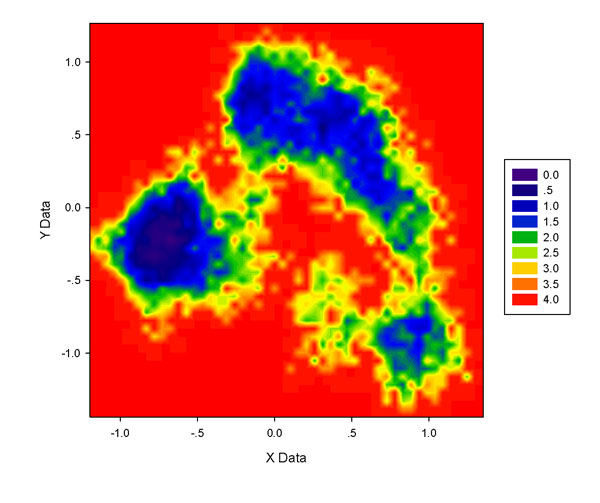
5.4 P=0的點對圖像的影響
為何要讓ddtpd輸出P=0的點需要說明一下,盡管這些點看似沒有意義。sigmaplot會對輸入的數據點的空隙進行差值使圖像平滑。如果P=0的區域都不輸出,這么大范圍的數據空缺區域sigmaplot都會通過插值來彌補。但由于空缺區域往往過大,插值出的結果經常很糟糕。下圖是75*75格點,不含P=0的點時sigmaplot給出的結果,和前面的圖相對比,會發現在數據點集中分布的區域周圍多出了一些的東西(如圖的左下角),尤其是在圖的中心偏左下的位置多出現一塊深藍區域,如果將它解釋為自由能很低的區域就明顯錯了,這都是因為sigmaplot插值所致。
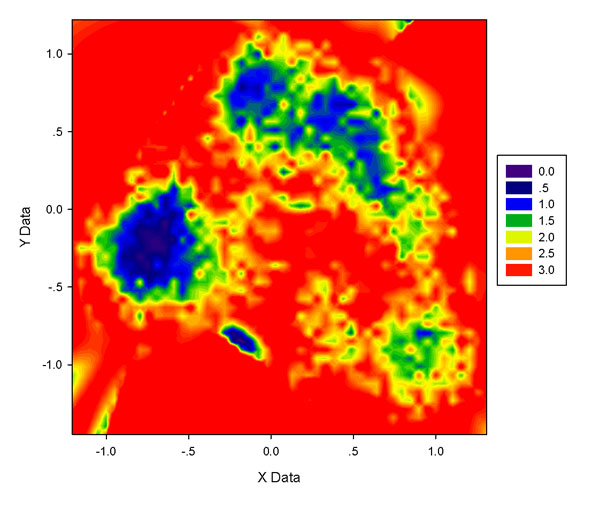
5.5 對數據點進行高斯展寬
如果用g_anaeig的時候加上-skip 10,就代表每10幀輸出一次投影值,前例有10000個點,此時就只有1000個點了,。這樣少的數據點很難做出滿意的圖,哪怕只用50*50格點,圖像仍然零碎,尤其是右上角的一片區域,如下圖所示。如果進一步降低格點數,圖像就不好看了。這時需要利用ddtpd的高斯展寬功能來改善。
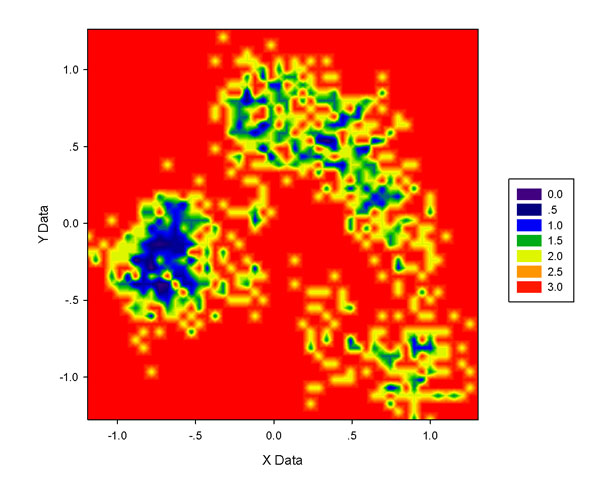
所謂高斯展寬,就是把每個點改成用高斯函數來表達(經過歸一化),簡單來說,比如一個格子內沒有數據點,而附近的某個格子內有1個數據點,那么這個格子也能分享到零點幾個數據點。這樣就不會造成數據點分布密集區域中由于恰好有一些格子沒有數據點(格點密度高的時候這種情況尤甚),而使圖像出現一堆窟窿或者顯得零碎。下圖是經過高斯展寬后的圖,明顯數值連續性比上圖好很多。為了效果更好,圖中色彩刻度設為了-1~4.5。
此圖做法是啟動ddtpd,依次輸入:
2dskip10.xvg //文件名
50 //將X軸劃分的格子數
50 //將Y軸劃分的格子數
4 //輸出將數據點經過高斯展寬后的-LnP
1 //展寬系數,默認是1,其值越大展寬效果越明顯,但會造成細節區域越難以顯現,可反復嘗試。假設輸入的是k,就代表展開成的高斯函數的半高寬是k*sqrt(dx^2+dy^2),其中dx和dy分別是X/Y方向的網格寬度。
y //輸出P=0的點
y //調整G的零點
注意屏幕上提示數據的最大值為5.11,20.305551對應P=0區域的值。對于利用高斯展寬得到的結果,作圖前將P=0區域的值替換成最大值就行了(不用再加1.0~1.5),此例即把result2.txt里的20.305551都替換為5.11,然后放到sigmaplot里作圖,調調色彩刻度即得到上圖。