使用Multiwfn計算分子片段的偶極矩和復合物中單體的偶極矩
使用Multiwfn計算分子片段的偶極矩和復合物中單體的偶極矩
文/Sobereva@北京科音 2020-Jun-23
1 原理
時不時有人問怎么計算一個分子中某些片段的偶極矩,或者問怎么計算一個分子復合物中各個分子的偶極矩,確實這對于分析局部的極性很有意義,在本文就通過例子對做法進行說明。做這種分析必須使用2020-Jun-22之后更新的Multiwfn程序,可以在http://www.shanxitv.org/multiwfn免費下載,相關基本知識看《Multiwfn FAQ》(http://www.shanxitv.org/452)和《Multiwfn入門tips》(http://www.shanxitv.org/167)。此功能需要使用含有波函數信息的文件作為輸入文件,比如wfn、wfx、mwfn、fch、molden等,產生的方式見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。
簡單來說,計算一個體系中由某些原子構成的片段F的偶極矩矢量就是計算
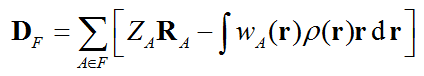
其中R是原子核位置,Z是原子核電荷,ρ是電子密度,w是原子的權重函數。計算片段偶極矩矢量需要用Multiwfn的主功能15(模糊空間分析),目前支持Hirshfeld、Becke、Hirshfeld-I形式的原子權重函數。本文就用比較常用,而且物理意義比較清楚的Hirshfeld權重函數來算。
需要注意的是,如果某個片段的凈電荷不為零,則這個片段的偶極矩是有原點依賴性的,即平移體系會令它發生改變。多數情況下被計算的片段的凈電荷不為0,卻也沒有辦法完全避免原點依賴性,只能是在討論的時候留意這個問題,予以恰當討論。
筆者之前還寫過一篇與本文有一定關系的文章《使用Multiwfn+VMD繪制片段貢獻的躍遷偶極矩矢量》(http://www.shanxitv.org/396),感興趣者推薦看看,這對于考察體系的不同區域對電子激發的振子強度的影響很有益。
2 計算分子片段的偶極矩實例
本節計算下面這個單重態[Ru(bpy)3]2+陽離子體系的各個配體的偶極矩,其wfn文件可以在這里下載:http://www.shanxitv.org/attach/558/Ru_bpy_3.zip。此文件的結構使用BP86泛函結合SDD和6-31G*進行優化,波函數用B3LYP結合SDD和6-311G*在IEFPCM模型描述的水環境下產生。此體系分子結構如下:
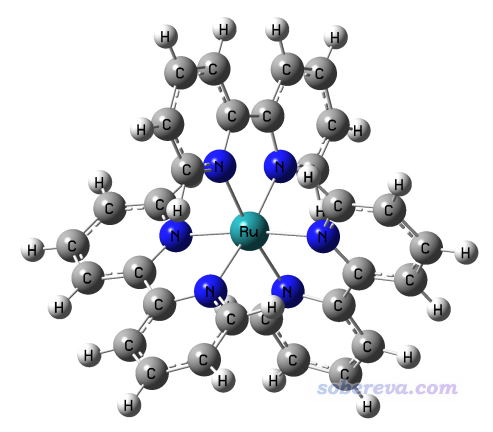
啟動Multiwfn后載入Ru_bpy_3.wfn,然后依次輸入
15 //模糊空間分析
-1 //選擇原子權重函數
3 //基于內置原子密度的Hirshfeld權重函數
-5 //定義功能1、2計算時考慮的原子范圍
2-21 //體系中一個配體里的原子序號
2 //計算原子和分子多極矩
此時Multiwfn依次計算各個原子的多極矩,最后給出這些原子對應的片段的電子數、偶極矩和不同形式的多極矩:
***** Molecular dipole and multipole moments *****
Total number of electrons: 81.427849
Molecular dipole moment (a.u.): -0.000000 4.348703 0.000000
Molecular dipole moment (Debye): -0.000000 11.053300 0.000000
Magnitude of molecular dipole moment (a.u.&Debye): 4.348703 11.053300
Molecular quadrupole moments (Standard Cartesian form):
XX= -41.258381 XY= -0.000000 XZ= -15.828189
YX= -0.000000 YY= -13.049129 YZ= -0.000000
ZX= -15.828189 ZY= -0.000000 ZZ= -33.042376
Molecular quadrupole moments (Traceless Cartesian form):
XX= -18.212629 XY= -0.000000 XZ= -23.742283
YX= -0.000000 YY= 24.101250 YZ= -0.000000
ZX= -23.742283 ZY= -0.000000 ZZ= -5.888621
Magnitude of the traceless quadrupole moment tensor: 25.129610
Molecular quadrupole moments (Spherical harmonic form):
Q_2,0 = -5.888621 Q_2,-1= -0.000000 Q_2,1= -27.415227
Q_2,-2= -0.000000 Q_2,2 = -24.429930
Magnitude: |Q_2|= 37.189945
Molecular octopole moments (Cartesian form):
XXX= 0.0000 YYY= -455.8273 ZZZ= -0.0000 XYY= -0.0000 XXY= -217.0765
XXZ= 0.0000 XZZ= 0.0000 YZZ= -176.7460 YYZ= 0.0000 XYZ= -85.0737
Molecular octopole moments (Spherical harmonic form):
Q_3,0 = -0.0000 Q_3,-1= -20.8698 Q_3,1 = 0.0000
Q_3,-2= -329.4892 Q_3,2 = -0.0000 Q_3,-3= -154.4790 Q_3,3 = 0.0000
Magnitude: |Q_3|= 364.5030
這些量的具體定義看Multiwfn手冊3.18.3節,這里不細說。我們當前關心的只有
Molecular dipole moment (a.u.): -0.000000 4.348703 0.000000
這一行,即偶極矩矢量為(0.0,4.3487,0.0) a.u.。
然后我們計算其它片段的偶極矩,依次輸入
-5 //重新定義片段
42-61
2 //計算原子和分子多極矩
-5 //重新定義片段
22-41
2 //計算原子和分子多極矩
匯總一下,三個配體的偶極矩分別為:
2-21片段: ( 0.000000 4.348703 0.000000) a.u.
42-61片段:( 3.766463 -2.173911 0.001788) a.u.
22-41片段:(-3.766463 -2.173911 -0.001788) a.u.
下面,我們用VMD程序將偶極矩的箭頭畫出來以便于觀看。VMD可以在http://www.ks.uiuc.edu/Research/vmd/免費下載,本文用的是VMD 1.9.3。wfn格式沒法載入VMD,所以我們先把當前體系轉換為VMD可以載入的xyz格式。在當前Multiwfn窗口中輸入
0 //返回主菜單
100 //其它功能(Part 1)
2 //導出文件
2 //導出為xyz格式
直接按回車用默認路徑,然后Ru_bpy_3.xyz就產生在當前目錄下了。
將Ru_bpy_3.xyz載入VMD,然后將Multiwfn的examples\scripts目錄下的drawarrow.tcl里的全部內容復制到VMD文本窗口里,這樣就定義了一個新的名為drawarrow的命令,我們用這個命令來繪制片段偶極矩。
在VMD的文本窗口里運行以下命令
draw color green
drawarrow "serial 2 to 21" 0.000000 4.348703 0.000000 0.7
draw color red
drawarrow "serial 42 to 61" 3.766463 -2.173911 0.001788 0.7
draw color yellow
drawarrow "serial 22 to 41" -3.766463 -2.173911 -0.001788 0.7
這些命令代表分別用綠、紅、黃色箭頭把三個片段偶極矩繪制出來。雙引號里面是選擇相應片段里的原子的選擇語句,語法詳見《VMD里原子選擇語句的語法和例子》(http://www.shanxitv.org/504)。之后的三個參數是偶極矩的X/Y/Z分量,最后的參數0.7是在繪圖時把偶極矩數值乘上這個系數再繪制,起到控制箭頭長度、令圖像美觀的目的。繪制出來的圖像如下。分子的顯示方式可以在Graphics - Representation界面調節。
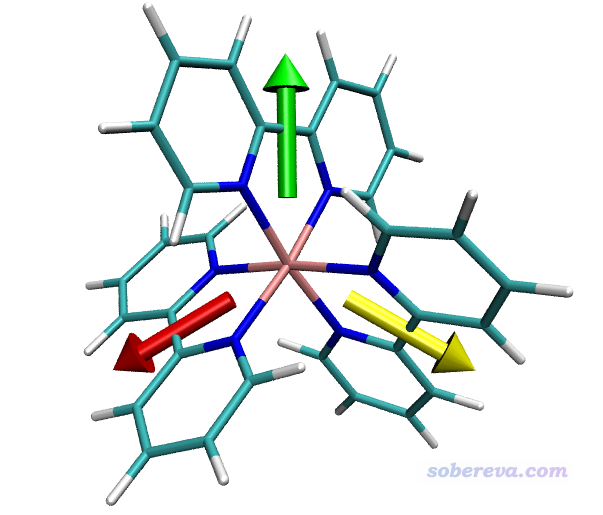
偶極矩是從負電中心指向正電中心。由圖可見每個片段的始端都是兩個氮的方向,這是因為氮帶負電,而且有豐富的孤對電子。顯然當前的結果完全合理。
如果之后想刪掉箭頭,在文本窗口運行draw delete all命令。
值得一提的是,當前這個體系里三個片段的偶極矩是對稱分布的,這是因為中心金屬正好在坐標原點上。由于每個配體的凈電荷不為零,因此如果在做產生波函數的任務之前把體系平移一下,最終得到的三個箭頭就不以Ru為中心對稱了。所以要注意原點位置問題。
有讀者問如果片段里的原子序號是不連續的怎么輸入。假設片段里原子序號是4,9-15,89-100,111,上面例子里的雙引號里就寫serial 4 9 to 15 89 to 100 111,即把-替換為[空格]to[空格],把逗號替換為[空格],即可。
3 計算分子復合物中單體偶極矩實例
下面這個例子我們計算一下苯酚二聚體中每個苯酚單體的偶極矩,并且連同二聚體的總偶極矩一起用VMD畫出來。
啟動Multiwfn,然后輸入
examples\phenoldimer.wfn //自帶的苯酚二聚體波函數文件
15 //模糊空間分析
-1 //選擇原子權重函數
3 //Hirshfeld
2 //計算原子和分子多極矩
由于我們當前還沒定義片段,所以Multiwfn最后給出的下面的信息直接就是二聚體的偶極矩了
Molecular dipole moment (a.u.): 1.227306 -0.128087 0.650833
之后和上一節的例子一樣,對第一個苯酚(1~13號原子)和第二個苯酚(14~26號原子)分別計算片段偶極矩,結果分別為(0.570356 -0.356257 0.284025) a.u.和(0.656950 0.228171 0.366808) a.u.。這兩個苯酚的偶極矩的矢量和與前面輸出的二聚體的偶極矩是相同的。
和前例一樣,把當前結構導出成xyz文件并載入VMD,并且把drawarrow.tcl里的內容拷到VMD的文本窗口里運行,之后輸入以下命令進行繪制:
draw color green
drawarrow all 1.227306 -0.128087 0.650833 2
draw color red
drawarrow "serial 1 to 13" 0.570356 -0.356257 0.284025 2
draw color yellow
drawarrow "serial 14 to 26" 0.656950 0.228171 0.366808 2
這些語句代表二聚體的偶極矩用綠色箭頭繪制,all代表整個體系。兩個苯酚的偶極矩分別用紅色和黃色繪制。由于苯酚的偶極矩較小,為了讓圖中箭頭足夠長,所以命令末尾用了2來讓箭頭長度變成偶極矩大小的兩倍。
得到的圖像如下
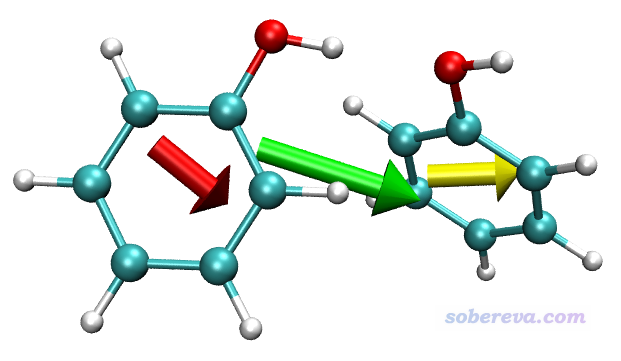
可見由于兩個苯酚的偶極矩的方向基本相同,二者的矢量和所對應的二聚體的偶極矩比單體偶極矩大得多。