在Gaussian中自定義范圍分離泛函的方法

在Gaussian中自定義范圍分離泛函的方法

First release: 2020-May-1 Last update: 2022-Nov-17

0 前言

之前筆者在《優化長程校正泛函w參數的簡便工具optDFTw》（http://www.shanxitv.org/346）介紹過長程校正泛函和明顯影響其結果的ω參數（以下簡寫為w）。在Gaussian中對DFT泛函自定義w值的做法在此文里也說了：《Gaussian中非內置的理論方法和泛函的用法》（http://www.shanxitv.org/344）。鑒于偶有人問怎么調節范圍分離泛函CAM-B3LYP的α和β參數、怎么在Gaussian里用LC-PBE0這樣短程HF成份不為0的泛函，筆者在此文就對Gaussian中自定義范圍分離泛函參數的問題專門說一下。在說具體怎么實現之前先回顧一下基本概念，否則讀者肯定會糊涂。本文內容是針對Gaussian 16而言的，對于其它版本可能適用也可能不適用。

自定義泛函需要用到IOp。在這里特意囑咐一下，Gaussian做多步任務時，IOp設置僅對第一個任務生效。因此用自定義泛函做opt freq任務時，freq任務是接收不到IOp的，會導致freq和opt用的不是同一個泛函，造成嚴重問題。因此自定義泛函時opt和freq必須分別做。

1 1/r12算符的劃分

對GGA泛函做長程校正(long range correction, LC)的思想最早由Tsuneda等人于JCP, 115, 3540 (2001)提出，它將描述電子間相互作用的1/r12算符做如下劃分，其中w直接影響被歸屬于長程和短程作用的范圍。erf是誤差函數（error function），介紹見https://en.wikipedia.org/wiki/Error_function。隨著自變量從0開始增加，erf也從0開始逐漸趨于1。

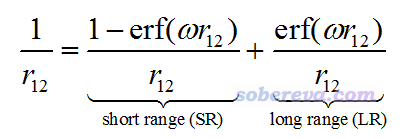
最早的LC類型的泛函將長程部分完全用HF交換項描述，短程部分完全用GGA交換泛函描述，這樣做局限性較大，在改進里德堡激發、電荷轉移激發等GGA泛函算得很差的問題的精度的同時顯著降低了對其它問題的計算精度。在2004年CAM-B3LYP的原文中，提出了Coulomb-attenuating method (CAM)形式的1/r12算符的劃分，如下所示

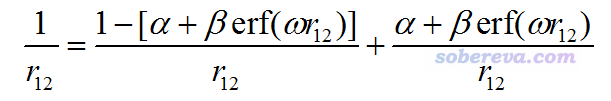
CAM比起LC額外引入了α和β參數，使得優化泛函參數的自由度更大，也令CAM-B3LYP泛函不像LC泛函那樣在熱化學數據計算精度等方面精度下降得那么嚴重。如今流行的wB97XD等泛函都是用的CAM的形式。在CAM形式下，長程極限的HF成份是α+β，短程極限的HF成份是α。全局雜化泛函相當于β=0、HF成份為α的情況。LC泛函相當于α=0、β=1的情況。

在JCP, 127, 221103 (2007)提出的HISS原文中，對1/r12的劃分還引入了中程區域：

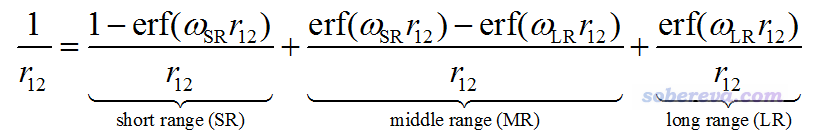
可見w參數有SR和LR兩種。當w_SR和w_LR相同時，這種劃分還原成LC的形式，當二者不同時，就有了一部分中程區域了。如果w_SR和w_LR其一為0，則這種劃分沒意義。這種含有中程區域的劃分沒太大實際價值，也就HISS等極少泛函使用。

范圍分離（range-separated）泛函這個詞泛指在不同電子作用距離下HF交換項、DFT交換泛函引入程度不同的泛函，上面這些提到的都屬于范圍分離泛函。范圍分離泛函大多是在長程范圍引入比短程范圍更高比例的HF交換項，但也有HSE06、MN12-SX等長程HF成份為0而短程不為0的泛函，還有HISS那樣更特殊的只有在中程范圍HF成份不為0而在短程和長程范圍都為0的泛函。另外還有所謂的局域雜化泛函，在三維空間不同位置使用不同HF成份，比范圍分離泛函更為廣義，但實現起來很困難，也沒太大價值，有興趣的話可以看綜述WIREs Comput. Mol. Sci., e1378 (2018)，這不屬于本文的范疇。

2 在Gaussian中定義范圍分離泛函

Gaussian在自定義范圍分離泛函方面很靈活，但也因此規則相當繞，程序手冊和IOp手冊里也語焉不詳，在這一節筆者詳細捋一下思路。

最廣義形式的范圍分離泛函的交換能可以寫為下面這樣

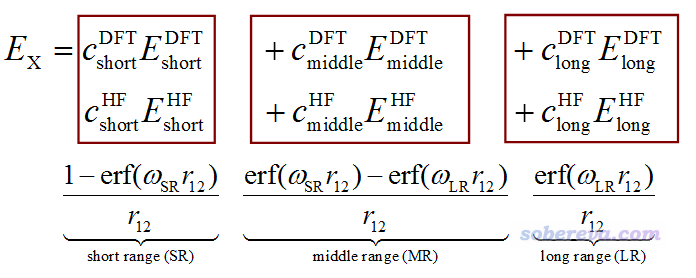
Gaussian里有以下IOp與定義范圍分離泛函的交換部分有關（雖然http://gaussian.com/overlay3/中也有相關說明，但說得不明不白），其中HFx代表HF交換項，DFx代表DFT交換項
IOp(3/107)：兩個數對應于HFx的wLong和wShort
IOp(3/108)：兩個數對應于DFx的wLong和wShort
IOp(3/119)：兩個數對應于HFx的cLong和cShort
IOp(3/120)：兩個數對應于DFx的cLong和cShort
IOp(3/138)：兩個數對應于DFxc和HFx的cMiddle
IOp(3/130)：對應于HFx的cFull
IOp(3/131)：對應于DFx的cFull
下面解釋一下這些項都是干嘛的。

Gaussian允許HF和DFT的交換部分用的w參數不同，但一般能見到的泛函對于DFx和HFx用的w參數是相同的，因此3/107和3/108定義的值總是相等的，它倆都設為MMMMMNNNNN就代表wLong為MMMMM/10000、wShort為NNNNN/10000。如果wLong或wShort其一為0，本質上就等于是wLong=wShort的情況，即不存在中程部分，此時也相當于只定義了一個w。例如w=0.47/Bohr的LC泛函就應該把3/107和3/108都寫為0470000000，即wShort=0、wLong=0.47，此時不存在中程部分。

Gaussian不是分別去對短程、中程和長程直接設置系數c，而是定義cFull、cLong、cShort。cFull+cLong對應長程系數，cFull+cShort對應短程系數。對于存在中程的情況，cFull相當于中程的系數。與CAM的定義對照，我們可知3/130設的HFx cFull對應于α參數、3/119設的HFx cLong對應于β參數。

如《Gaussian中非內置的理論方法和泛函的用法》（http://www.shanxitv.org/344）所述，Gaussian通過IOp(3/76=MMMMMNNNNN)來將全局雜化泛函的HF交換項系數設為NNNNN/10000，如果將這稱為ScaHFX，則
實際的短程HFx系數是ScaHFX*HFx_cShort，實際的長程HFx系數是ScaHFX*HFx_cLong。

根據Gaussian實際輸出信息，我發現對于wShort為0而只定義了wLong的情況，也就是絕大多數范圍分離泛函的情況，DFT交換部分用的系數實際上是：短程為1 - DFx cShort，長程為1 - DFx cLong。而其它情況下DFx cShort和DFx cLong都是直接定義的實際用的系數。

IOp(3/130=NNNNN)設置HFx cFull為NNNNN/10000的時候，如果令十萬、百萬、千萬位設1，說明分別將HFx cShort、HFx cLong、HFx cMedium取負。設置DFx的IOp(3/131)的用法也是如此。

Gaussian中通過IOp(3/77=MMMMMNNNNN)設置普通雜化泛函的LDA部分和GGA校正部分乘的系數，在定義范圍分離泛函的時候這兩部分必須相同，即MMMMM=NNNNN才行。

此外，Gaussian還支持對DFT相關部分(DFc)的范圍分離，如下所示，但這沒實際用處，不用管。
IOp(3/109)：兩個數對應于DFc的wLong和wShort
IOp(3/121)：兩個數對應于DFc的cLong和cShort
IOp(3/132)：對應于DFc的cFull

3 內置的一些范圍分離泛函解讀

使用范圍分離泛函做計算的時候寫上#P，就可以在SCF迭代開始前看到泛函的具體參數。下面我們看看對一些常見的范圍分離泛函Gaussian輸出的信息，弄懂了這些才好自定義

(1) LC-PBE 短程0%，長程100%，w=0.47：
IExCor=11009 DFT=T Ex=LC-PBE+HF Corr=PBE ExCW=0 ScaHFX= 1.000000
ScaDFX= 1.000000 1.000000 1.000000 1.000000 ScalE2= 1.000000 1.000000
HFx wShort= 0.000000 wLong= 0.470000 cFull= 0.000000 cShort= 0.000000 cLong= 1.000000
DFx wShort= 0.000000 wLong= 0.470000 cFull= 0.000000 cShort= 0.000000 cLong= 1.000000
可見HFx和DFx的w設置是一樣的，前面說了它倆總應當設一樣。wShort為0體現出此泛函沒有利用中程范圍，wLong就對應LC泛函的w了。此例短程HF成份為cFull+cShort=0%，而長程為cFull+cLong=100%。當前情況比較簡單，HFx和DFx的cShort、cLong參數都相同，說明HFx與DFx精確互補（別忘了如上一節所述，對wShort=0這種情況，在某個范圍DFx設的系數若為c，則真正用的系數為1-c）。

(2) CAM-B3LYP 短程19%，長程65%，w=0.33：
IExCor=20419 DFT=T Ex+Corr=CAM-B3LYP ExCW=0 ScaHFX= 1.000000
ScaDFX= 1.000000 1.000000 1.000000 0.810000 ScalE2= 1.000000 1.000000
HFx wShort= 0.000000 wLong= 0.330000 cFull= 0.190000 cShort= 0.000000 cLong= 0.460000
DFx wShort= 0.000000 wLong= 0.330000 cFull= 0.190000 cShort= 0.000000 cLong= 0.460000
可見w=0.33。短程HF成份是0.19+0.00=19%，長程是0.19+0.46=65%。此泛函的相關部分是LYP，其中LYP梯度校正部分的系數是0.81，這是ScaDFX后面第四個數為0.81的原因。關于這個在http://www.shanxitv.org/344中我已經說過了。此泛函的DFT交換項和HF交換項也是精確互補的。

(3) wB97X 短程15.77%，長程100%，w=0.3：
IExCor= 4538 DFT=T Ex+Corr=wB97X ExCW=0 ScaHFX= 1.000000
ScaDFX= 1.000000 1.000000 1.000000 1.000000 ScalE2= 1.000000 1.000000
HFx wShort= 0.000000 wLong= 0.300000 cFull= 0.157706 cShort= 0.000000 cLong= 0.842294
DFx wShort= 0.000000 wLong= 0.300000 cFull= 0.000000 cShort= 0.000000 cLong= 1.000000
顯然此泛函w=0.3。短程HF成分是0.1577+0.0=15.77%，長程HF成分是0.1577+0.8423=100%。此泛函的DFx和HFx的系數并非是精確互補的。DFx的cFull+cShort為0，因此在短程部分DFT交換項的實際系數為1。又由于DFx的cFull+cLong為1，因此在長程部分DFT交換項的實際系數為0。從wB97X原文28式可見，確實此泛函中DFT交換項只有短程部分。

(4) HISSbPBE（HISS）：
IExCor= 4709 DFT=T Ex+Corr=HISSbPBE ExCW=0 ScaHFX= 1.000000
ScaDFX= 1.000000 1.000000 1.000000 1.000000 ScalE2= 1.000000 1.000000
HFx wShort= 0.840000 wLong= 0.200000 cFull= 0.600000 cShort= -0.600000 cLong= -0.600000
DFx wShort= 0.840000 wLong= 0.200000 cFull= 0.400000 cShort= 0.600000 cLong= 0.600000
由于這個泛函特意考慮了中程作用，因此wShort與wLong不相等。中程HF成份為cFull=0.6=60%，短程HF成分為cFull+cShort=0.6-0.6=0%，長程HF成分為cFull+cLong=0.6-0.6=0%。HFx的系數靠3/119來定義時只能定義為正值，將之變成此例這樣的-0.6需要借助前述的3/130。由于wShort不為0，在這里顯示的DFx的系數，也即IOp直接設的DFx的系數就是實際用的系數，因此中程的DFx系數為cFull=0.4，短程部分系數是cFull+cShort=0.4+0.6=1，長程部分系數是cFull+cLong=0.4+0.6=1。可見，HISS泛函的HFx和DFx是精確互補的，在HF成份為0的短程和長程部分DFT交換項都為100%。

(5) HSE06 短程25%，長程0%，w=0.11：
IExCor= 3909 DFT=T Ex+Corr=HSEH1PBE ExCW=0 ScaHFX= 0.250000
ScaDFX= 1.000000 1.000000 1.000000 1.000000 ScalE2= 1.000000 1.000000
HFx wShort= 0.110000 wLong= 0.000000 cFull= 0.000000 cShort= 1.000000 cLong= 0.000000
DFx wShort= 0.110000 wLong= 0.000000 cFull= 0.000000 cShort= -0.250000 cLong= 1.000000
這是本文例子里唯一一個長程HF成份為0而短程不為0的泛函。此泛函沒有利用到中程區域，本質上就只利用了一個w=0.11，而輸出中顯示的wShort=0.11 wLong=0顯得比較莫名其妙。雖然此泛函的HFx的cFull+cShort=1，但由于ScaHFX=0.25（之前的泛函這項都是1），因此如前所述實際的短程HF成份為ScaHFX*(cFull+cShort)=0.25=25%。如HISS原文式8和表1所示，這個泛函的短程部分的DFT交換項系數是0.75，長程部分為1.0。而在當前的輸出中，DFx的cFull+cShort=-0.25，顯得有點莫名其妙。我的猜測是當這種數值為負值且wShort>wLong的情況，實際系數0.75是根據1-0.25計算出來的。DFT交換項的長程部分是cFull+cShort=0.0+1.0=1.0，這沒什么好說的。

4 自定義范圍分離泛函例子

這一節我們來通過IOp自定義兩個范圍分離泛函。

4.1 CAM-B3LYP

在一些文章中修改了CAM-B3LYP中的α和β參數，在修改之前我們先看看怎么才能“從頭”通過IOp來實現原始的CAM-B3LYP泛函。正確的關鍵詞是這樣的：
# BV5LYP/基組 IOp(3/76=1000010000,3/77=1000010000,3/78=0810010000) IOp(3/107=0330000000,3/108=0330000000) IOp(3/119=0460000000,3/120=0460000000) IOp(3/130=01900,3/131=01900)

上面為了清楚，把不同類別的IOp分開寫了，合寫到一起也完全可以。用這套關鍵詞進行計算時會看到輸出的泛函定義如下，和前面提到的直接用CAM-B3LYP關鍵詞時候顯示的各種系數都是相同的。
IExCor= 402 DFT=T Ex=B+HF Corr=LYP ExCW=0 ScaHFX= 1.000000
ScaDFX= 1.000000 1.000000 1.000000 0.810000 ScalE2= 1.000000 1.000000
HFx wShort= 0.000000 wLong= 0.330000 cFull= 0.190000 cShort= 0.000000 cLong= 0.460000
DFx wShort= 0.000000 wLong= 0.330000 cFull= 0.190000 cShort= 0.000000 cLong= 0.460000

下面詳細說說為什么定義。先回顧一下普通雜化泛函的定義方式（詳見http://www.shanxitv.org/344）：
E_XC = a*[ d*E_X_LDA + c*ΔE_X_GGA ] + b*E_X_HF + f*E_C_LDA + e*ΔE_C_GGA
這些系數通過IOp(3/76=ab)、IOp(3/77=cd)、IOp(3/78=ef)來設置。

CAM-B3LYP是將Becke88交換泛函、HF交換項以及LYP相關泛函進行組合得到的。因此我們先寫BV5LYP，其中B代表Becke88，V5LYP代表LYP。由于CAM-B3LYP原文里明確說用的是基于VWN5的LDA相關泛函定義的LYP，然而Gaussian默認的是基于VWN3的，因此必須刻意寫成V5LYP。此泛函里a是1，HF交換部分具體情況之后會按照范圍分離泛函的方式定義，故先將全局系數b設為1，因此用了3/76=1000010000。CAM-B3LYP里LDA交換部分和其GGA梯度校正部分的系數是相同的，并且具體情況之后會按照范圍分離泛函的方式定義，故先將全局系數c和d都設為1，因此用了3/77=1000010000。CAM-B3LYP的相關泛函部分的構成和B3LYP的相同，即LDA相關泛函的系數為1（f=1），再加上0.81的LYP形式的GGA梯度校正（e=0.81），因此用了3/78=0810010000。

CAM-B3LYP不對中程范圍單獨定義，且w為0.33，因此wShort應當設0，wLong應當設0.33，在加上如前所述HFx和DFx用的w一般情況下都是等同的，故用了3/107=0330000000和3/108=0330000000。原文里說了此泛函的α=0.19、α+β=0.65，即短程和長程HF成份分別為19%和65%。想實現這個，就令HFx的cFull等于α（即3/130=01900），令cLong等于β（0.46）且cShort等于0（即3/119=0460000000）。前面說過CAM-B3LYP的DFx與HFx是互補的，因此令定義DFx系數的3/120和3/131分別等于3/130和3/119即可。

把以上的討論弄清楚了，怎么像一些文獻中那樣基于其它的α和β參數做CAM-B3LYP計算就很清楚了。比如α=0.15、β=0.4、w=0.25，就用下面的關鍵詞即可：
BV5LYP IOp(3/76=1000010000,3/77=1000010000,3/78=0810010000) IOp(3/107=0250000000,3/108=0250000000) IOp(3/119=0400000000,3/120=0400000000) IOp(3/130=01500,3/131=01500)
其中3/76、3/77、3/78保持原CAM-B3LYP的定義不變，只修改了Overlay 3里面的107、108、119、120、130、131。

為了寫起來更簡便，也可以在CAM-B3LYP基礎上只重設w、α和β部分，也就是把上面的“BV5LYP IOp(3/76=1000010000,3/77=1000010000,3/78=0810010000)”這一堆直接用“CAM-B3LYP”關鍵詞來代替。

4.2 LC-PBE0

這個泛函在J. Chem. Phys., 129, 034107 (2008)提出，參數是w=0.3、α=0.25、α+β=1.0。它等于把PBE0和LC相結合，近程還是和PBE0一樣的25% HF成份，而長程則為100%。原先的PBE0等價于PBEPBE IOp(3/76=1000002500,3/77=0750007500)，將之改造為LC-PBE0，就寫：
PBEPBE IOp(3/76=1000010000,3/77=1000010000) IOp(3/107=0300000000,3/108=0300000000) IOp(3/119=0750000000,3/120=0750000000) IOp(3/130=02500,3/131=02500)
其中PBEPBE IOp(3/76=1000010000,3/77=1000010000)這部分相當于先把PBE泛函弄成全局100% HF交換+100% DFT交換的狀態，之后再用其它IOp定義不同范圍如何雜化。

當前關鍵詞下輸出的信息如下，可見很正確。
ScaDFX= 1.000000 1.000000 1.000000 1.000000 ScalE2= 1.000000 1.000000
IRadAn= 5 IRanWt= -1 IRanGd= 0 ICorTp=0 IEmpDi= 4
HFx wShort= 0.000000 wLong= 0.300000 cFull= 0.250000 cShort= 0.000000 cLong= 0.750000
DFx wShort= 0.000000 wLong= 0.300000 cFull= 0.250000 cShort= 0.000000 cLong= 0.750000