使用Gaussian+PySOC在TDDFT下計算旋軌耦合矩陣元
2018-Dec-29注:有不少人表示PySOC運行不了。只要讀者使用本文的操作系統、嚴格按本文的操作步驟計算,至少本文的例子是絕對能運行成功的。讀者應當先確保本文例子能運行正常,由此確認安裝方式和自己的操作過程無誤后再去跑你自己的體系。如果你當前沒有本文用的系統,可以用VMware虛擬機裝,半小時就能裝好。
2019-Feb-10注:筆者后來又寫了《使用ORCA在TDDFT下計算旋軌耦合矩陣元和繪制旋軌耦合校正的UV-Vis光譜》(http://www.shanxitv.org/462),用起來明顯比用Gaussian+PySOC方便得多,還更快、更準確,且完全免費,因此在筆者來看PySOC沒什么使用價值了,本文僅適合了解計算原理之用。讀者不要再以任何形式問筆者PySOC的使用問題,筆者不予回復,筆者一律建議用ORCA算SOC矩陣元。
使用Gaussian+PySOC在TDDFT下計算旋軌耦合矩陣元
文/Sobereva @北京科音
First release: 2018-Mar-15 Last update: 2019-Mar-30
0 前言
本文會簡要介紹旋軌耦合矩陣元的基本知識和計算原理,然后介紹怎么使用Gaussian結合完全開源免費的PySOC程序在研究激發態最常用的TDDFT方法下計算各個單-三重態之間的旋軌耦合矩陣元。其實PySOC使用起來一點也不難,希望看過此文的Gaussian用戶不會出現就為了計算旋軌耦合矩陣元而去買昂貴的ADF程序的情況。本文對于理論部分只是簡要提及,便于讀者能夠理解計算結果和計算意義,系統的相對論量子化學知識介紹可以參看相關專著,諸如Dyall寫的Introduction to Relativistic Quantum Chemistry就很好。限于篇幅和表達方式的限制,具體、細碎、系統的東西在文中不好呈現,相關內容會在北京科音(http://www.keinsci.com)的高級量子化學培訓班里講授。1 旋軌耦合矩陣元的基礎知識
薛定諤方程是標量方程,求解得到的波函數是“一分量”的。而考慮相對論效應時與薛定諤方程對應的叫做Dirac方程,解出來的波函數用含有四個分量的spinor(旋量)表示,體現出電子與正電子、alpha與beta自旋間的耦合。由于基于Dirac方程計算實際化學體系耗時較高(但也沒一些文章和書籍里說得那么離譜),為了使求解更容易進行,不同的人提出了不同方法將Dirac方程進行變換,使四分量哈密頓中的電子和正電子部分脫耦合,從而得到描述電子部分的二分量方程,此時其alpha和beta自旋還是耦合在一起的。變換成二分量的方法非常多,諸如FW(Foldy-Wouthuysen)、X2C、ZORA(Zero-order regular approximation)、DK(Douglas-Kroll)、IOTC等。這些二分量哈密頓算符可以寫為非相對論部分、標量相對論部分和旋軌耦合(H_SO)這三類算符的加和。因此,旋軌耦合本質上來自于相對論效應。在不考慮相對論效應的情況下,電子波函數的空間部分和自旋部分是可以分離的。旋軌耦合體現的是電子自旋與電子軌道運動的相互作用,因此當考慮旋軌耦合算符后,電子波函數的空間和自旋部分就不能分離了。因此,當考慮旋軌耦合后,就沒有諸如單重態、三重態這樣的概念了。當不考慮旋軌耦合時,不同自旋多重度之間的態之間哈密頓矩陣元精確為0,換句話說就是沒有相互作用。但是把旋軌耦合算符引入哈密頓之后,不同自旋多重度的態之間就可以發生相互作用,因此最終得到的本征態將是不同自旋多重度的態的線性組合。
所謂旋軌耦合矩陣元,就是指<i|H_SO|j>這種積分,它體現出i、j兩個電子態之間的旋軌耦合作用的大小。在能夠計算旋軌耦合矩陣元的一些程序和計算了旋軌耦合矩陣元的文章中,它往往也被稱為旋軌耦合常數(但注意旋軌耦合常數這個詞也有其它指代)。
計算旋軌耦合矩陣元有什么用?最常見的用處就是通過微擾方式計算磷光發射速率或磷光壽命。磷光發射是三重態激發態到單重態基態的躍遷,當不考慮旋軌耦合時,由于這兩個態自旋部分正交,因此計算躍遷偶極矩時候結果精確為0,導致振子強度為0,故是躍遷禁阻的。而當以微擾的方式考慮旋軌耦合的時候,則單重態里面就會摻進去一定三重態成份,而三重態里面會摻進去一定單重態成份,因此再計算躍遷偶極矩的時候,由于會引入單-單重態和三-三重態的躍遷偶極矩,因此結果就不嚴格為0了。至于具體如何通過本文計算的旋軌耦合矩陣元計算磷光速率,筆者之后會另文介紹。此外,計算旋軌耦合矩陣元還被用于考察系間竄越速率(正比于相應兩個態之間旋軌耦合矩陣元的模方),通過二階微擾方法還可以通過旋軌耦合矩陣元計算多重態因為旋軌耦合效應導致的子態的能級分裂(這被稱為ZFS,零場分裂)。
計算旋軌耦合矩陣元的時候H_SO的算符定義并不唯一,取決于用什么方法把Dirac方程變換為二分量。把Dirac方程對于分子體系最完整的哈密頓形式,即Dirac-Coulomb-Breit哈密頓做FW變換得到的是Breit-Pauli (BP)哈密頓,多數程序里和文獻里都是取BP哈密頓中的旋軌耦合算符H_SO來計算旋軌耦合矩陣元,常用的ORCA也是如此,這樣處理比較簡單。但也有其它情況,比如Dalton程序也支持用DK哈密頓的旋軌耦合算符來計算,而ADF則是基于ZORA來計算。
很多程序都可以計算旋軌耦合矩陣元。大多數程序支持的是在MCSCF或多參考方法級別下計算,比如ORCA、GAMESS-US、Molpro、Molcas等。然而眾所周知,這類方法不黑箱,需要使用者能夠恰當定義活性空間,而且計算較耗時,用于諸如較大的配合物體系比較困難。然而,具有較強磷光發射能力的體系大多卻正是含有過渡金屬的配合物體系,這類體系主流的研究手段是TDDFT。因此,在TDDFT下計算旋軌耦合矩陣元這一點非常重要。可惜的是,能做到這點的程序很有限。常見的就三個,一個是賊貴的ADF,一個是雖然開源免費,但是使用門檻比ADF高得多的Dalton,還有一個是ORCA,在這方面做得很好,見《使用ORCA在TDDFT下計算旋軌耦合矩陣元和繪制旋軌耦合校正的UV-Vis光譜》(http://www.shanxitv.org/462)。
Gaussian在旋軌耦合計算方面是個顯著軟肋,只支持MCSCF下計算旋軌耦合矩陣元,而且還很不好用。好在,在J. Chem. Theory Comput., 13, 515?524 (2017)一文中,作者發布了一個名為PySOC的開源免費的小工具,可以基于Gaussian的TDDFT的輸出文件在TDDFT級別下計算旋軌耦合矩陣元,解決了很多人長期發愁的一大問題,使用方法將在本文后面詳細介紹。
2 旋軌耦合矩陣元的一些特點
旋軌耦合矩陣元是個復數,有虛部也有實部,有些程序(如ADF)會分別輸出這兩部分,有的程序(如PySOC)則只給出它的模,即實部和虛部的平方和開根號。旋軌耦合算符可寫為其x、y、z三個分量加和的形式,多數量化程序(如ORCA、Dalton等)會分別計算、分別輸出;而有的程序(如PySOC)并不分別計算并分別輸出,而是在計算的時候就合在一起了。三個分量有的對應實部有的對應虛部,程序在給出三個分量時經常將虛部用負數表示。
我們最關心的一類旋軌耦合矩陣元是單重態與三重態間的,PySOC計算的也正是這種矩陣元。之所以三重態叫三重態,是因為它包含三個子態(sublevel),自旋磁量子數分別為+1、0和-1。單重態與三重態的不同子態之間的旋軌耦合矩陣元并不相同。有的程序(如PySOC)會分別輸出單重態與每個子態的旋軌耦合矩陣元,也有的程序只給出總大小,相當于單重態與每個子態旋軌耦合矩陣元的平方和開根號。
由于旋軌耦合矩陣元數量級比較小,因此一般用cm^-1為單位表示,與常用單位的轉換關系是:1Hartree=219474.6363cm^-1、1eV=8065.5447cm^-1。
3 關于旋軌耦合積分
確定了H_SO的形式,就可以計算兩個電子態之間的旋軌耦合矩陣元了。通過推導,它可以寫為基函數間的旋軌耦合算符對應的積分(旋軌耦合積分)的線性組合,組合系數涉及軌道展開系數和組態系數。H_SO其中包含單電子旋軌耦合算符H_SO1和雙電子旋軌耦合算符H_SO2,前者體現電子自旋與它繞著原子核的軌道運動的耦合,后者體現電子自旋與這個電子繞著其它電子的軌道運動的耦合。前者很好算,花不了什么時間,然而對于較大體系,計算后者耗時非常高,牽扯到雙電子積分的導數。然而,H_SO1和H_SO2的貢獻都在同一個數量級,若直接忽略后者甚至能對旋軌耦合矩陣元帶來達到1/3程度的誤差。為了降低雙電子旋軌耦合積分的耗時,有人提出自旋軌道平均場(SOMF)的處理方法,修改了H_SO2算符的形式,使得雙電子旋軌耦合以平均場的方式近似計算(類似于Hartree-Fock的思想),這使耗時大為降低,而帶來的誤差可忽略不計(對于不是特別重的原子來說)。這種自旋軌道平均場的做法在實際量化程序中一般是以稱作Atomic-mean field integral (AMFI)的方式具體實現的,在計算時只保留SOMF的單中心項,使得耗時更低,盡管誤差也會稍大一點。
有效原子電荷(Zeff)方法也是非常常用的近似計算旋軌耦合積分的方法。它的思想是,由于實際研究發現H_SO1和H_SO2部分有比較好的比例關系,因此,可以修改H_SO1項,來把H_SO2的效果等效地吸入H_SO1里面。這樣僅需要花費計算H_SO1項的耗時,就可以同時體現出H_SO2的效果了。Zeff這種做法是目前最便宜的考慮旋軌耦合的做法,比AMFI便宜得多,但是誤差比較明顯,可能能達到百分之十幾、二三十甚至更多(和體系、元素、參數有關。對于很重的過渡金屬誤差可能較大)。Zeff的還一個很大好處是可以結合贗勢使用來節約耗時,同時等效考慮標量相對論效應。比如計算一個Pt的配合物,如果用Zeff,那么可以給Pt用相對論贗勢,這樣即便不用相對論哈密頓,Au的標量相對論效應也考慮了,而且在此基礎上通過很便宜的Zeff方式就能把旋軌耦合效應也考慮了,真是美哉!反之,用AMFI的時候不僅考慮旋軌耦合這部分相對更昂貴,對Pt還得用全電子基組(算一個的耗時頂得上算一把輕原子),而且雪上加霜的是還得用相對論哈密頓考慮標量相對論效應。可見,以Zeff方式計算旋軌耦合積分來得到旋軌耦合矩陣元,對于大體系是很理想的做法。雖說精度差一些,但對于大體系來說,一般也沒必要那么較真。
使用Zeff的一個關鍵是有效電荷。把H_SO2的效果吸入H_SO1就是通過把H_SO1里面原子核電荷改為有效電荷來實現的。有效電荷是前人擬合出來的,比如可以通過計算一批體系的零場分裂能,通過令計算值和實驗值盡可能相符來得到。有效電荷的好壞直接影響Zeff方法的精度,而且,僅當要算的元素有已經擬合好的有效電荷的時候才能用Zeff方法處理。有效電荷的數值一定程度上受到當初擬合它用的計算級別的影響,但影響不至于特別大,只要自己用的基組和當初在擬合時相差不是特別大就可以用,比如當初是在6-31G*下擬合的,你結合cc-pVDZ、def2-SVP、6-311G*等使用也沒問題。有些有效電荷是對于贗勢基組來擬合的,你用的時候可以結合其它贗勢基組用,但你用的贗勢和擬合時候用的贗勢所贗化的內核電子數必須相同,比如不能當初是對小核贗勢基組擬合的有效電荷,你卻結合大核贗勢基組來用。
有不同的人提出不同的有效電荷,最常用的一套是Koseki在90年代搞的一套。在JPC, 96, 10768 (1992)中對6-31G*擬合了前三周期元素有效電荷,在JPC, 99, 12764 (1995)中對SBKJC贗勢擬合了一直到碘的所有主族的有效電荷,在JPCA, 102, 10430 (1998)中對SBKJC贗勢擬合了所有d、ds族過渡金屬的有效電荷。擬合時候都是用MCSCF做的,結合如今常用的DFT也沒什么問題。SBKJC贗勢如今不怎么用,它對過渡金屬是小核,對主族是大核,在Gaussian里直接寫SDD、lanl2所用的贗勢也是這種情況,因此可以把這套有效電荷搭配常用的SDD、lanl2贗勢來用。
4 PySOC的特征和原理
PySOC可以在https://github.com/jzpathfinder/pysoc下載。程序雖然開頭倆字母是py,強調程序里用了Python,但實際上大部分都是Fortran寫的。此程序的主要用處是結合Gaussian計算TDDFT級別下的單重態-三重態間的旋軌耦合矩陣元,基態要求是閉殼層單重態。程序目前支持G09,筆者發現似乎沒法正常處理G16的輸出(網友提供了可以兼容G16的方法,見http://bbs.keinsci.com/thread-19813-1-1.html)。PySOC應當也可以在Windows下用,但本文都只涉及Linux的情況。PySOC實際上還支持DFTB+程序,DFTB+是用來做DFTB方法的計算的。DFTB從精度和速度上類似于半經驗版的DFT,將DFTB和TDDFT弄在一起就是TD-DFTB,耗時比一般的TDDFT低得多。根據PySOC原文的測試,基于TD-DFTB得到的旋軌耦合矩陣元比起TDDFT的相差很多,并沒什么卵用,所以本文也不去談怎么把PySOC和DFTB+結合使用。
PySOC的運作機制是這樣的:首先用戶用Gaussian09做TDDFT計算得到同等數目的單重態和三重態激發態,并保留rwf文件。然后啟動PySOC.py,這個腳本就會調用Gaussian自帶的rwfdump工具從rwf文件中提取各種接下來用的信息,比如組態系數、分子軌道展開系數,并且從Gaussian輸出文件中提取一些信息,比如激發能、基組定義。然后PySOC自動調用附帶的修改版MolSOC以Zeff方式計算旋軌耦合積分,這里MolSOC是一個可以獨立運行的專門用來計算旋軌耦合積分的程序。接下來PySOC就按照其原文里的公式,將旋軌耦合積分、組態系數、分子軌道展開系數組合到一起,得到包含基態在內的各個單重態與各個三重態激發態間的旋軌耦合矩陣元。
原版的PySOC和原版的MolSOC都有一些不完美的地方,于是筆者進行了修改,下文一切操作的步驟一律都是相對于這里提供的修改版來說的。筆者的PySOC+MolSOC修改版下載地址:http://www.shanxitv.org/soft/sob_PySOC_MolSOC.zip
筆者的修改版相對于原版在功能上主要有以下改變:
1 把SOC矩陣元輸出文件的態的序號輸出格式改為了兩位(原版只留了一個字符的位置,因此態數如果是兩位數就會被顯示為星號,不便考察)
2 PySOC默認會計算激發態之間的躍遷偶極矩,但是這沒什么用,而且筆者發現雖然對于TDA計算得到的躍遷偶極矩是正確的,但是對于TD計算,得到的躍遷偶極矩并不合理。于是筆者刪除了計算這個的功能,PySOC計算大體系的總耗時由此可降低約40%。PS:如果真需要計算激發態間的躍遷偶極矩,可以用Multiwfn,結果可靠,速度也快。見《利用Multiwfn計算Gaussian輸出的激發態之間的躍遷偶極矩》(http://www.shanxitv.org/227)。
3 修改了MolSOC里定義有效電荷的sozeff.f文件。此程序自帶的有效電荷是其作者自己擬合的前五周期主族的(用B3LYP結合DZVP全電子基組下擬合,見JCC,30,832 (2009)),以及極個別其它零碎的元素。顯然只有這些有效電荷根本不夠用,結合贗勢算配合物都不行。筆者遂把上面提到的所有Koseki擬合的有效電荷都補充進去了。
5 PySOC的安裝、配置
用PySOC最好系統別太老,否則一方面系統自帶的Python版本太老會導致PySOC的Python腳本無法正常運行(要求Python版本>=2.7,可以用python --version命令查看本機python版本),另一方面由于PySOC和MolSOC預編譯版是在較新的系統下編譯的,在老系統上運行會因為找不到較新的glibc庫而出錯。筆者建議用CentOS/RHEL >7.0版。如果是較老的系統,也可以升級Python,并且自己編譯PySOC和MolSOC。注:很多本文的讀者反映PySOC沒運行成功,很大一部分是因為用的Python版本問題不合適所致的。筆者這里用的CentOS 7.2自帶的Python是2.7.5版。如果你運行不成功,嘗試用這個或相近版本的Python。
首先將修改版的PySOC+MolSOC解壓,比如PySOC解壓后的目錄為/sob/pysoc,MolSOC解壓后的目錄為/sob/molsoc_modified。分別進入這兩個目錄,都運行chmod +x * -R命令,使這倆目錄和子目錄下的所有文件都有可執行權限。
把pysoc/bin/pysoc.py里的scrip_soc變量改為實際的PySOC可執行文件路徑,比如scrip_soc = '/sob/pysoc/bin'。對于當前情況,/sob/pysoc/bin目錄里面會看到有個soc_td,這正是筆者編譯出來的PySOC中由Fortran寫的代碼對應的可執行文件。
修改/sob/pysoc/input_template/init.py,把腳本里的g09root改為g09所在目錄(和安裝Gaussian時的g09root環境變量指向的路徑一致),把molsoc_path改為實際的修改版molsoc的路徑,比如molsoc_path = '/sob/molsoc_modified/molsoc0.1/bin/molsoc0.1.exe'。
修改用戶目錄下的.bashrc文件,添加export PATH=$PATH:/sob/pysoc/bin/。之后重新進入終端,就可以在任意目錄下直接輸入pysoc.py來調用這個運算腳本了。
進入/sob/molsoc_modified/molsoc0.1/bin目錄,會看到有三個可執行文件,對應不同有效電荷的情況,你當前的計算適合哪種情況,就把哪個可執行文件改名為molsoc0.1.exe。這三個文件對應的情況為:
molsoc0.1_1.exe:保留了作者自己對前五周期主族擬合的有效電荷(用于全電子計算,對DZVP擬合),加入了Koseki對d、ds族金屬結合SBKJC小核贗勢擬合的有效電荷
molsoc0.1_2.exe:保留了作者自己對前三周期擬合的有效電荷,對第四、五周期主族改為了Koseki對SBKJC大核贗勢擬合的有效電荷,加入了對d、ds金屬koseki對小核SBKJC贗勢擬合的有效電荷。
molsoc0.1_3.exe:把前三周期元素改為了Koseki對6-31G*擬合的有效電荷,對第四、五周期主族改為了Koseki對SBKJC大核贗勢擬合的有效電荷,加入了對d、ds金屬koseki對小核SBKJC贗勢擬合的有效電荷。
一般來說,推薦用molsoc0.1_3.exe,對應于前三周期都用全電子基組,而對之后的元素用SDD、lanl2等贗勢的情況,這是最常見的情形。
再次提醒,使用PySOC在用贗勢的時候,贗化的電子數一定要和SBKJC對應,缺乏基礎知識的話仔細看《贗勢的函數形式以及在量子化學程序中定義的方式》(http://www.shanxitv.org/188)、《談談贗勢基組的選用》(http://www.shanxitv.org/373)、《在贗勢下做波函數分析的一些說明》(http://www.shanxitv.org/156)。比如你把molsoc0.1_3.exe改名為了molsoc0.1.exe以令PySOC能夠調用它,若你要計算個含碘的體系,那對碘就不能用def2系列或者cc-pVnZ-PP系列了,因為它們對主族是小核,而Koseki擬合有效電荷時用的SBKJC對主族是大核。
如果你想自己編譯PySOC也可以,最好用ifort編譯器。在/sob/pysoc/src目錄下,修改Makefile里的編譯器和庫的目錄,然后直接運行make,就會產生soc_td,將之挪到/sob/pysoc/bin目錄下就可以用了。
如果要自己編譯MolSOC,就進入/sob/molsoc_modified/molsoc0.1/source源代碼目錄,里面會看到有sozeff_1.f、sozeff_2.f、sozeff_3.f三個文件,它們是用來設定有效電荷的,分別對應于上述molsoc0.1_1.exe、molsoc0.1_2.exe、molsoc0.1_3.exe的情況,打算用哪套有效電荷組合就把哪個.f文件改名為sozeff.f。之后運行make來編譯,默認會調用ifort編譯,并產生可執行文件/sob/molsoc_modified/molsoc0.1/source/molsoc0.1.exe。
6 PySOC的使用
用PySOC計算旋軌耦合矩陣元之前需先自行用Gaussian09運行TD(50-50,nstates=x)任務計算單重態和三重態各x個,x設多大up to you。由于程序只能處理笛卡爾型基函數,因此必須寫上6d 10f關鍵詞。雖然程序手冊里沒明確強制要求,但實際發現nosymm也得寫,否則PySOC貌似沒法正常解析輸出文件。另外還得寫GFInput讓Gaussian把基組定義輸出出來。輸出文件名字必須為gaussian.log,并且必須保留下來rwf文件,名字為gaussian.rwf。以下是輸入文件開頭部分的例子:%rwf=gaussian.rwf
# td(50-50,nstates=5) wB97X/TZVP 6D 10F nosymm GFInput
注:PySOC對態數、泛函沒有任何限制,但是由于MolSOC只支持角動量<=f的基函數的旋軌耦合積分的計算,因此用的基組不能包含f以上角動量基函數(由于高角動量函數對于TDDFT計算以及旋軌耦合矩陣元的影響很小,這個要求無關大礙)。
G09算完后,確保gaussian.rwf和gaussian.log都在當前目錄了,將init.py從/sob/pysoc/input_template里拷到當前目錄下,然后用文本編輯器打開它。Gaussian做TD(50-50)計算時nstates設了幾,就把此文件里n_s =和n_t =后面的序列從1一直寫到多少。比如nstates設了5,init.py里就要設n_s = [1, 2, 3, 4, 5]和n_t = [1, 2, 3, 4, 5]。有的時候我們可能要算幾十個態,手動從1寫到最后相當麻煩,為了方便大家使用,我把從1到100的序號附到這個文件里了,并在開頭加了#來注釋掉。比如算了40個態,想計算S0~S40與T1~T40之間的旋軌耦合矩陣元,那就把從1到40的序號復制到n_s和n_t后面的方框里就行了。
最后,運行pysoc.py即可,程序就會根據當前目錄下init.py的信息利用gaussian.rwf和gaussian.log文件進行運算了,屏幕上輸出的都是一堆爛七八糟對用戶沒什么用的debug信息。PySOC的計算耗時和體系大小、計算的態數都有關系,小體系一兩分鐘就能算完,而大體系、上百個態的情況甚至需要算半個小時乃至更多。可惜PySOC沒有被并行化,沒法利用多核的優勢。算的態數很多的時候,建議以諸如pysoc.py > pysoc.out方式運行來把輸出信息重定向到某個文件里,要不然可能由于屏幕上輸出信息量太大導致拖慢計算。
算完后當前目錄下會看到一大堆文件,有的是PySOC調用rwfdump導出的數據,有的是MolSOC程序的輸入輸出文件,有的是PySOC運行產生的一些中間信息。其中soc_out.dat是最重要的輸出文件,這就是各個態之間的旋軌耦合矩陣元。這是其中一條輸出:
sum_soc, <S0|Hso|T1,1,0,‐1> (cm‐1): 115.94270 81.98387 0.01644 81.98387
代表S0和T1之間總SOC是115.94 cm-1,它由這行后面的<S0|Hso|T1_Ms=1>、<S0|Hso|T1_Ms=0>、<S0|Hso|T1_Ms=-1>三個值求平方和開根號得到,這里Ms指T1子態的自旋磁量子數。另外當前目錄下還會產生ene_out.dat,這里面是各個態的激發能。
下面我們通過兩個實例演示怎么使用PySOC。本文所有Gaussian計算用的都是G09 E.01 Linux版,系統是CentOS 7.3。計算前讀者應當根據本文第5節的方式把PySOC運行環境進行了恰當配置、恰當修改了相關的.py文件。下面例子用的有效電荷對應的是上文提到的molsoc0.1_3.exe的情況(即用戶已經把此文件改名為了molsoc0.1.exe)。更老的G09版本筆者未經測試,建議不要用老于D.01版的,尤其是早期G09程序的TD(50-50)選項有bug,PySOC肯定運行不正常。
7 實例1:計算H2CO的單-三重態間的旋軌耦合矩陣元
本例我們考察一個很簡單的體系,甲醛。在PySOC原文的表3中,給出了這個體系的計算結果,如下所示
首先我們在PBE0/TZVP級別下優化甲醛分子,輸入文件如下。
# PBE1PBE/TZVP opt
test
0 1
C 0.00000000 0.00000000 -0.56221066
H 0.00000000 -0.92444767 -1.10110537
H -0.00000000 0.92444767 -1.10110537
O 0.00000000 0.00000000 0.69618930
然后把優化好的結構保存成新的Gaussian輸入文件,內容如下,所用計算級別和原文表3一致。雖然我們只需要考察S1和T2,但正如《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》(http://www.shanxitv.org/314)中所提到的,算的態數不應當正好卡著要研究的態。如果感興趣的是第i態,那么計算到i+3態一般是比較穩妥的,因此本例我們總共計算5個單重態和5個三重態。
%rwf=gaussian.rwf
# td(50-50,nstates=5) B3LYP/TZVP 6D 10F nosymm GFInput
test
0 1
C 0.00000000 0.00000000 -0.52513500
H 0.00000000 0.93987900 -1.11261300
H 0.00000000 -0.93987900 -1.11261300
O 0.00000000 0.00000000 0.67200400
運行g09 < H2CO.gjf > gaussian.log,算完后當前目錄下就有了gaussian.log和gaussian.rwf。然后把/sob/pysoc/input_template/init.py文件拷到當前目錄,用文本編輯器打開它,確認n_s和n_t都被設為了[1, 2, 3, 4, 5]。然后,直接輸入pysoc.py命令來運行之,由于體系很小而且考慮的態數也很少,眨眼間就算完了。屏幕上最后會提示有報錯“forrtl: severe (153): allocatable array or pointer is not allocated”,這沒有關系,這是因為筆者的修改版把PySOC計算躍遷偶極矩的部分給去掉了所致,這不影響旋軌耦合矩陣元的輸出。
打開當前目錄下產生的soc_out.dat,從中會看到這行
sum_soc, <S 1|Hso|T 2,1,0,-1> (cm-1): 49.81285 0.00000 49.81285 0.00000
即其中第一個數字49.81285 cm-1就是總的<S1|H_SO|T2>矩陣元。這個值和文獻中的45 cm-1略有偏差,原因是原文計算時候并沒有修改MolSOC里默認的有效電荷,即用的是MolSOC作者自己搞的有效電荷,而我們現在用的則是Koseki擬合的有效電荷。可見有效電荷的不同,對于結果是會產生一定影響的,但影響不至于很大。倘若我們運行pysoc.py之前是把molsoc0.1_1.exe改名為了molsoc0.1.exe,即計算H,C,O元素的時候用MolSOC作者自己搞的有效電荷,結果將為44.73483 cm-1,和PySOC原文里的精確一致。
8 實例2:計算Os配合物的單-三重態間的旋軌耦合矩陣元
有較強發磷光能力的分子一般都是含有靠后周期的d金屬的配合物,因為這樣的金屬會引入顯著的旋軌耦合效應,這類配合物體系是需要考察單-三重態旋軌耦合的主要場合之一。Gaussian+PySOC以Zeff方式計算這類體系是否靠譜?我們這里重現一下Phys. Chem. Chem. Phys., 16, 26184 (2014)文章里的旋軌耦合數據。此文研究了一系列含有Os、Au、Cu、Ag的配合物,通過Gaussian在B3LYP/6-31G*結合lanl2DZ做了幾何優化,然后使用ADF在B3LYP結合TZP全電子基組并考慮ZORA標量相對論效應下算了最低10個單重態和三重態,之后計算了激發態間的旋軌耦合矩陣元。計算時候都以PCM模型考慮了二氯甲烷的溶劑效應。此文考察了不少體系,為了節約時間,我們就考察其中比較小的Os-4,結構如下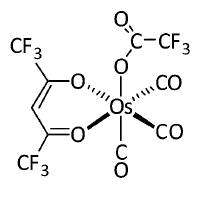
本節例子涉及的文件都可以在此下載:Os-4.rar
首先我們用gview等程序構建Os-4結構,保存輸入文件,優化此體系同時做振動分析確認無虛頻。我們用的計算級別和原文一致,輸入文件如下(其實Os用SDD會更好,參見《談談贗勢基組的選用》http://www.shanxitv.org/373)
# B3LYP/genecp opt freq scrf(solvent=CH2Cl2)
[...略]
C O F H
6-31G*
****
Os
lanl2DZ
****
Os
lanl2DZ
將優化后的結構保存成新的輸入文件,做電子激發計算。我們用的泛函和原文一樣也是B3LYP,也是算最低10個單重態和三重態。原文用的是ADF,這程序很非主流,其基組都是基于Slater函數的,因此文中用的TZP基組在Gaussian這樣的基于高斯函數的程序中沒有嚴格對應的。我們這里就用基于高斯函數的3-zeta基組中質量上乘的def2-TZVP來做計算(這對于當前計算來說其實有點浪費了),整體和TZP能達到同一個檔次。由于def2-TZVP對Os是小核贗勢基組,筆者的修改版MolSOC里又加入了Koseki對所有d族對小核贗勢擬合的有效電荷,因此此時正好可以用PySOC來計算(如果在Gaussian里用更昂貴、更準確的DKH2標量相對論方法結合全電子基組來做此體系的TDDFT計算,PySOC則沒法用,因為沒有對MolSOC添加對過渡金屬全電子基組擬合的有效電荷)。
Os-4的電子激發計算輸入文件如下(Os-4_TD.gjf)
%rwf=gaussian.rwf
# b3lyp/def2TZVP scrf(solvent=CH2Cl2) TD(nstates=10,50-50) 6d 10f nosymm gfinput
[...略]
然后運行g09 < Os-4_TD.gjf > gaussian.log。由于用的基組較大,因此耗時還是不短的。算完后把init.py拷到當前目錄,把其中的n_s和n_t后面都改為[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],然后運行pysoc.py > pysoc.out,過一會兒就算完了。
文獻中在表1中給出了各個Os配合物發生主要系間竄越的兩個態之間的旋軌耦合矩陣元,對Os-4給出的是<S1|H_SO|T2>,數值為620 cm-1,在S0結構下它們的能級差(即垂直S1-T2能級差ΔE_ST)為0.11eV。
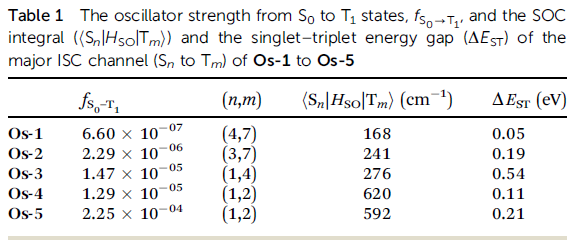
我們看看我們算的。打開ene_out.dat,會看到S1和T2能量分別為3.9079eV和3.9945eV,能級差為0.09eV,和文獻給出的值之間的絕對差異很小。然后打開soc_out.dat,會看到
sum_soc, <S 1|Hso|T 2,1,0,-1> (cm-1): 593.44440 419.62830 0.69267 419.62830
即我們算出來的<S1|H_SO|T2>為593cm-1,和文獻給出的620cm-1之間的相對誤差才不到5%。雖然相符這么好不免有些巧合,但至少也足夠說明我們用的贗勢+Zeff的廉價考慮標量相對論效應和旋軌耦合效應的組合對于配合物是可靠的。
筆者在更廉價的基組上也做了計算測試,配體用6-311G*,Os用SDD,這個檔次對此體系耗時僅為def2-TZVP時的1/4,算出來的<S1|H_SO|T2>為539.9cm-1,ΔE_ST=0.093eV。可見單-三重態能級差用6-311G*結合SDD已經足夠算準,旋軌耦合矩陣元對基組更敏感點,但當前級別至少也足夠給出定性合理的結果。
9 總結
Gaussian+PySOC這種組合可以很容易地計算TDDFT級別下的旋軌耦合矩陣元,雖然PySOC計算本身也花時間,但耗時比TDDFT過程低一個數量級,即曰只要TDDFT算得動,單-三重態旋軌耦合矩陣元就可以輕易獲得。雖然PySOC的結果基于比較糙的Zeff方法,但精度對于考察包括過渡金屬配合物在內的較大體系來說夠用了。
如果你不是非得用Gaussian不可,那么相對于本文的做法,用ORCA是好得多的選擇,更快、更方便還更準確,看《使用ORCA在TDDFT下計算旋軌耦合矩陣元和繪制旋軌耦合校正的UV-Vis光譜》(http://www.shanxitv.org/462)。
免費的Dalton也可以算TDDFT下的單-三重態旋軌耦合矩陣元,但門檻稍高,而且算激發態間的旋軌耦合矩陣元耗時遠高于用Gaussian+PySOC或ORCA。