基頻頻率校正因子實際效果測試

之前寫過一篇《談談諧振頻率校正因子》（http://www.shanxitv.org/221）專門介紹了量化計算中頻率校正因子的原理、類型和正確的使用方式。在本文中，將通過一系列五花八門的雙原子分子的頻率計算結果和實驗數據的對比，來讓讀者更好地了解頻率校正因子以及非諧振計算的效果。本文不打算做系統性、大規模、嚴謹的全面測試，能以小見大就夠了。

本文選取的一系列分子來自http://cccbdb.nist.gov/expdiatomics.asp，根據實驗測定的雙原子分子光譜常數ωe、ωexe、ωeye，可以容易地得到實驗諧振頻率和基頻頻率。真實諧振頻率就是ωe，真實基頻頻率按照如下方式可得到

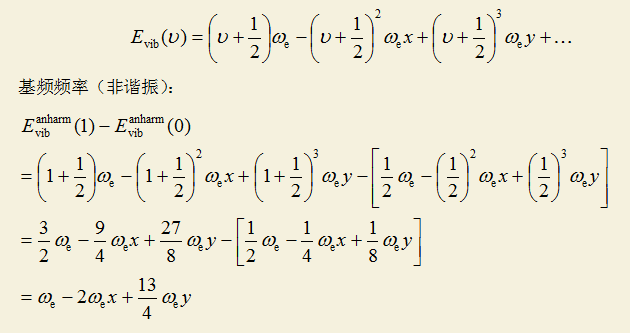
測試共選取了15個分子，特征相差較大，用的都是基態。除了O2是三重態、TiO是三重態、VO是四重態、AlO是二重態以外，其它的都是單重態。用的是最常用的B3LYP泛函做的計算，考慮了兩種基組，一種是便宜的6-31G*，一種是高質量的def2-TZVP。以下是計算結果，單位都是cm-1。“校正后”是freq關鍵詞直接輸出的諧振頻率乘上校正因子后得到的，“非諧振”是用Gaussian的VPT2方式得到的非諧振頻率（寫freq=anharm關鍵詞即可得到）

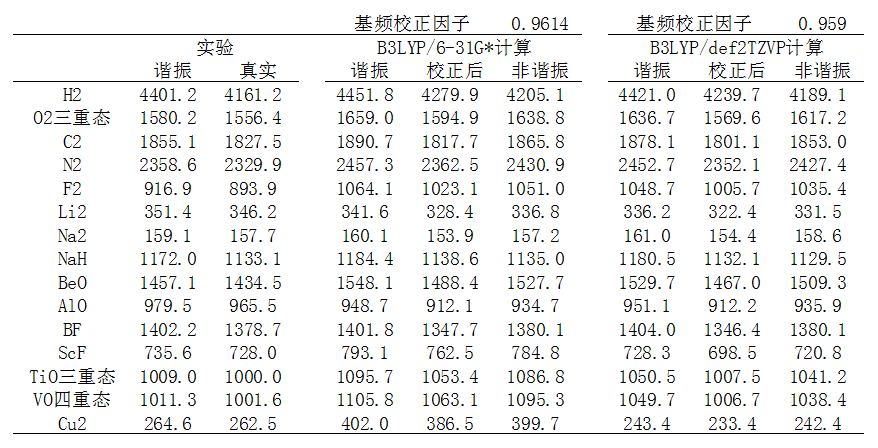
下面是B3LYP/6-31G*計算值相對于實驗值的誤差，MSE是平均含符號誤差，MUE是平均無符號誤差（即先取絕對值再取平均）。為了敘述方便，下述的“真實頻率”指的是“實驗測定的非諧振頻率”，即振動光譜直接測得的頻率。

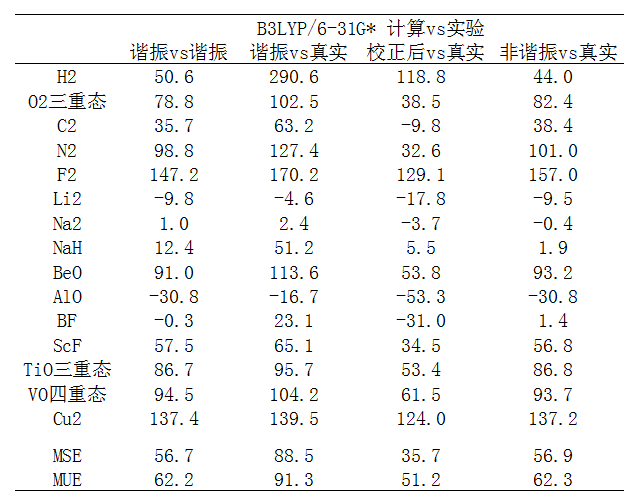
由數據可見，即便不考慮非諧振問題，從MSE上看光是B3LYP/6-31G*計算的諧振頻率本身就比實驗的諧振頻率整體偏高，也因此，文件中報道的用于令B3LYP/6-31G*諧振頻率盡可能與實驗諧振頻率相符的校正因子是個小于1的值（0.991）。

從“諧振vs真實”的數據來看，直接算出來的諧振頻率與真實頻率相差是很大的，MSE值體現出整體有著顯著的高估。但是高估多少，和體系關系非常大，諸如對H2能高估290cm-1，而對Na僅高估2cm-1。此級別的諧振頻率也并非一定高估，諸如計算的AlO諧振頻率甚至低于真實頻率，不過這種情況甚少。

“校正后vs真實”是指把計算的諧振頻率乘上基頻校正因子后與真實頻率的差值。從MSE上看到，校正因子的效果使得系統性高估的問題顯著減輕了，從88.5cm-1降低到35.7cm-1，而且從MUE上看，此時精度也比不考慮基頻校正因子時有了很大改進。這充分說明基頻校正因子的重要性。但是，也不要忽視個例，比如AlO原本計算的諧振頻率就比真實頻率低，考慮校正因子后低估得更多了，誤差反倒還更大了。

我們再來看看直接用VPT2方法算的非諧振頻率與真實頻率的差異，即“非諧振vs真實”所示的那一列。從MSE結果上看，雖然也整體高估頻率，但比不考慮非諧振效應的時候好很多。不過，VPT2非諧振計算需要計算能量的四階導數，對稍微大一點的體系都是非常昂貴的，而整體精度，從MSE和MUE上可以看到還不如直接把諧振頻率乘上頻率校正因子的做法好。只不過對某些體系，比如H2，做非諧振計算比起諧振頻率乘以校正因子的結果好很多，前者誤差是44cm-1，后者是118.8cm-1，所以非諧振計算依然有其價值。

總的來說，基頻校正因子是非常有價值的，確實能令諧振近似下的頻率與真實頻率整體相符得明顯更好，但是這個校正因子卻不是萬能的，從“校正后vs真實”的數據可以看到最終誤差有大有小，是顯著依賴于體系特征的。在B3LYP/6-31G*級別，經過校正后誤差仍超過100cm-1的有H2、F2和Cu2，而且后兩個的非諧振頻率誤差也同樣很大。

如果用高質量基組會是什么情況？下面看B3LYP/def2-TZVP的結果與實驗的對比

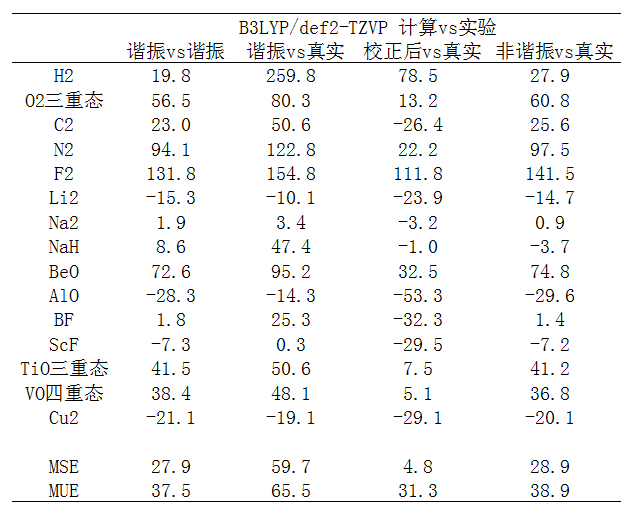
從數據看，不管怎么比，不管是MSE還是MUE，def2-TZVP下的結果與實驗值的誤差都低于6-31G*，雖然仍整體高估但是高估程度降低了不少，而且絕對誤差也減小了。6-31G*下Cu2算得巨爛，不僅頻率誤差大，優化出來的鍵長也很糟糕。實驗值是2.2197埃，而優化的結果是2.0244埃，相差高達1/10！實際上，6-31G*算第一周期過渡金屬靠后的元素表現較差，特別是Co、Ni、Cu爛，在很老的文章J. Chem. Phys., 118, 7775里就已經指出了。切換到def2-TZVP后，優化的結果2.2909埃，和實驗相符很好，而且頻率計算結果也和實驗值相符多了。然而對于F2，即便用了def2-TZVP，頻率誤差僅很小幅降低，無論是利用頻率校正因子還是做非諧振計算，高估真實頻率都很明顯，這明顯就是當前用的理論方法的問題了。對比6-31G*和def2-TZVP的結果，我們會看到改善基組使得誤差降低得最多的是涉及過渡金屬的體系，不僅Cu2，連TiO、VO的結果也大幅改進。有的人說文獻里的頻率校正因子不適合含過渡金屬的體系，但從當前的結果來看，這種說法不實，如果他們發現結果在乘了基頻校正因子后很爛，則很可能在計算的時候用的基組對相應元素描述得太low（如6-31G*描述Cu）。

我在很多地方強調過，B3LYP/6-31G*結合頻率校正因子的結果就已經夠用了。諸多文獻里的測試數據也表明，在考慮頻率校正因子的前提下，提升基組質量并不會對結果有什么改進，費力不討好。但本文的結果似乎與此矛盾。實際上，這主要原因是本文的測試體系太雜，五花八門，還包含過渡金屬，因此用更好的基組來試圖避免因基組質量過低導致出現很大誤差是有意義的。但如果純粹只著眼有機體系，由于不同體系間電子結構差異沒有那么顯著，而且有機體系本身比較好描述，用頻率校正因子容易系統性地修正，在考慮頻率校正因子時def2-TZVP的結果并不會比6-31G*有顯著進步。