Molcas的計算雙原子分子光譜常數的模塊vibrot使用簡介
計算雙原子分子的轉動-振動譜涉及的光譜常數是量子化學研究雙原子分子體系常涉及的。Molcas程序自帶了一個不錯的vibrot模塊,專門用來計算這些量,使用時只需要直接提供離散的勢能面掃描的數據即可,完全不依賴于Molcas的其它模塊。另外它還可以計算其它信息,包括振動波函數、轉-振態間的躍遷性質、溫度平均下的可觀測量(需要提供事先算好的不同鍵長時對應的可觀測量的數值,如偶極矩)。
本文將以氟化氫HF為例簡要介紹一下vibrot模塊怎么用。如果對下面計算的一堆雙原子分子光譜常數的含義不了解的話,推薦先看看筆者寫的這個文檔:/usr/uploads/file/20170417/20170417174516_16229.pdf
首先要做的是用自己擅用的量化程序在較合適的級別下對分子的勢能面進行掃描,獲得極小點附近一片區域內的勢能信息,得到一套離散的“坐標 能量”數據點。數據點可以均勻分布也可以不均勻分布,vibrot會基于它們做三次樣條插值構建勢能面。顯然,要考察越高的振動能級,掃描的鍵長范圍就應該越大,如果還要讓程序輸出準確的解離能,那就需要掃描距離的上限值相當大才行。這里筆者通過Gaussian在UCCSD(T)/cc-pVQZ級別下對HF鍵長進行掃描,從1 Bohr開始掃到4 Bohr,步長0.1 Bohr。之所以用Bohr為單位是因為vibrot在輸入數據的時候要求以Bohr為單位。(如果只在平衡距離較近范圍內掃描,閉殼層CCSD(T)就足夠好,由于這里掃描上限較大,故用UCCSD(T),這樣超過不穩定點后會比閉殼層CCSD(T)好得多。當然還有更理想但也更昂貴或更麻煩的選擇,如TCCSD、MRCI等)。
之后基于掃描的勢能數據寫一個文本文件vibHF.txt作為vibrot的輸入文件,內容如下,這是個非常典型的輸入文件。下面只做簡要注釋,完整的選項和說明看手冊
&VIBROT
RoVibrational spectrum //一般設這個
Title = UCCSD(T)/cc-pVQZ curve for HF //標題
Atoms = 0 H 0 F //體系包含H和F,前頭的0代表用最大豐度的同位素的質量
Potential //下面提供每個鍵長(Bohr)時的能量(Hartree),自由格式,數目不限
1 -0.99838084467D+02
1.1 -0.10004327670D+03
1.2 -0.10017757133D+03
1.3 -0.10026413004D+03
1.4 -0.10031822868D+03
1.5 -0.10035010691D+03
1.6 -0.10036672296D+03
1.7 -0.10037285786D+03
1.8 -0.10037182747D+03
1.85 -0.10036895106D+03
1.9 -0.10036595106D+03
2 -0.10035686368D+03
2.1 -0.10034572525D+03
2.2 -0.10033336186D+03
2.3 -0.10032036301D+03
2.4 -0.10030714974D+03
2.5 -0.10029402321D+03
2.6 -0.10028119928D+03
2.7 -0.10026883299D+03
2.8 -0.10025703618D+03
2.9 -0.10024588825D+03
3 -0.10023544681D+03
3.1 -0.10022575237D+03
3.2 -0.10021683281D+03
3.3 -0.10020870635D+03
3.4 -0.10020138218D+03
3.5 -0.10019486293D+03
3.6 -0.10018914421D+03
3.7 -0.10018421457D+03
3.8 -0.10018005645D+03
3.9 -0.10017664428D+03
4 -0.10017394551D+03 //這一行之后的選項都是可選的,不設就用默認值
Plot = 1.0 10.0 0.1 //輸出插值出來的勢能曲線,分別是初值、終值、步長
VIBRational = 3 //考慮最低3個振動量子數,即v=0,1,2
ROTAtional = 0 3 //考慮的轉動量子數范圍為J=0,1,2,3
Grid = 300 //輸出的振動波函數包含的點數
Range = 1.0 4.0 //輸出的振動波函數的距離下限和上限
PRWF //將振動波函數直接打印到輸出文件中
運行此命令,調用molcas執行上面的輸入文件:molcas vibHF.txt > vibHF.out
一瞬間就算完了。輸出的.xml和.status文件都不用管,vibHF.VibWvs是二進制的振動波函數數據,當前我們不用管它。vibHF.VibPlt0里面是基于插值產生的勢能曲線數據。vibHF.out包含了我們最感興趣的信息,比較重要的部分下面說一下。
以下是插值出的勢能曲線的極小點位置和勢能值,以及外推到無窮遠處的勢能值
extremum points
R(au) Value
Min point 1.731435 -100.373181
Extrapolated value at infinity -100.127233
下面這部分是各個振動+轉動態的能量相對于勢能曲線最小點的數值(Hartree)
Eigenstates
Vib. q.n. Rot. q.n. Energy
0 0 0.009399 //v=0,J=0的值。相當于ZPE
1 0 0.027559 //v=1,J=0的值,即第一振動激發態的振動能
2 0 0.044934
0 1 0.009586
1 1 0.027739
2 1 0.045108
0 2 0.009961
1 2 0.028100
2 2 0.045455
0 3 0.010523
1 3 0.028641
2 3 0.045976
轉動常數B和離心畸變常數D是依賴于振動量子數的,諸如下面輸出的是v=0的振動態對應的值。
Rotational constants for vibrational quantum number 0
B=0.205907E+02 cm-1 D=0.210149E-02 cm-1
再往下的三行是基于v=0振動態的B和D計算的其J=1,2,3的轉動態的轉動能(雖然我們設的計算范圍包括J=0,但它對應的轉動能為0。所以不輸出),計算公式在前面我提供的文檔里就有。第三列是按照公式算出來的值,最后一列是第2、3列的差值。
Observed and computed term values (cm-1)
1 0.411731E+02 0.411730E+02 0.801538E-05
2 0.123469E+03 0.123469E+03 -0.445299E-05
3 0.246786E+03 0.246786E+03 0.890598E-06
下面是把前面輸出的v=0,1,2時對應的B和D匯總到一起重新輸出了一次
Rotational constants B(nv) and D(nv) in cm-1
1 0.205907E+02 0.210149E-02
2 0.198229E+02 0.204650E-02
3 0.190734E+02 0.199452E-02
下面是計算D所需的De和βe值,以及由此算出的對應v=0,1,2時的D值(第三列)。
Spectroscopic constants De=0.212773E-02 cm-1 Betae=-.534833E-04 cm-1
Observed and computed D values
0 0.210149E-02 0.210099E-02 0.502747E-06
1 0.204650E-02 0.204750E-02 -0.100549E-05
2 0.199452E-02 0.199402E-02 0.502747E-06
下面是計算B所需的Be、αe和γe值,以及由此算出的對應v=0,1,2時的B值(第三列)。
Spectroscopic constants Be,Alphae and Gammae
Be=0.209815E+02 cm-1 Alphae=0.786143E+00 cm-1 Gammae=0.916029E-02
Observed and computed B values
0 0.205907E+02 0.205907E+02 -0.461853E-13
1 0.198229E+02 0.198229E+02 0.710543E-14
2 0.190734E+02 0.190734E+02 0.188294E-12
下面是計算振動能級所需的振動常數we、wexe、weye,以及由此算出的對應v=0,1,2時的振動能級(第三列)。
Vibrational constants we =0.417438E+04 cm-1
wexe=-.990961E+02 cm-1 //注意這里和習俗不同。負號本不應當體現在這個wexe數值里面,而是應體現在振動能級的計算公式里
weye=0.290290E+01 cm-1
Observed and computed band origins
0 0.206278E+04 0.206278E+04 -0.609361E-10
1 0.604840E+04 0.604840E+04 -0.499313E-09
2 0.986195E+04 0.986195E+04 -0.106047E-08
下面是上面輸出過的最重要的雙原子分子光譜常數匯總。De(ev)和D0(ev)后面分別是平衡解離能和完全解離能的數值。但由于我們掃描的勢能曲線范圍不是很遠,最遠才4 Bohr,還明顯沒達到水平區域,所以這里給出的De和D0不要太當真,只有掃描到很遠的情況這倆數值才準。
Re(a) 0.9162 //平衡坐標(埃)
De(ev) 6.6922 //當前級別下嚴格計算值為6.07eV,故這個外推值高估了
D0(ev) 6.4365
we(cm-1) 0.417438E+04
wexe(cm-1) -.990961E+02
weye(cm-1) 0.290290E+01
Be(cm-1) 0.209815E+02
Alphae(cm-1) 0.786143E+00
Gammae(cm-1) 0.916029E-02
Dele(cm-1) 0.212773E-02 //之前輸出的時候符號是De,這里為了避免和平衡解離能混淆所以改了符號
Betae(cm-1) -.534833E-04
如果感興趣的話,可以去NIST網站上搜一下HF的雙原子常數的實驗值,和我們算的來對照,在這個頁面就能看到http://webbook.nist.gov/cgi/cbook.cgi?ID=C7664393&Units=SI&Mask=1000。從中看到,基態電子態的光譜常數值為Re=0.91680,we=4138.32,wexe=89.88,Be=20.9557,αe=0.798,De=0.2151E-02,我們算的與實驗值大多都符合得不錯或很好,除了wexe誤差略大,達到9.3%。
輸出信息再往后是各個(v,J)組合相對于極小點的能量,J對應列,v對應行,其實之前就已經輸出過了,這里只不過是把單位換成cm-1再輸出一次。
Term values(observed and computed) in cm(-1)
J-value 0 1 2 3
v-value
0 2062.78 2062.78 2103.95 2103.95 2186.25 2186.25 2309.56 2309.56
1 6048.40 6048.40 6088.03 6088.03 6167.26 6167.26 6285.98 6285.98
2 9861.95 9861.95 9900.09 9900.09 9976.32 9976.32 10090.54 10090.54
再往后是各個(v,J)組合時的振動波函數。比如下面是J=0時的v=0,1,2的情況,距離的單位是Bohr。vibrot是通過Numerov方法求解二階微分方程來得到這些振動波函數的。
Rotational quantum number J= 0
Radial dist. v= 0 1 2
1.000000 0.00000344 0.00001530 0.00004470
1.004663 0.00000361 0.00001606 0.00004687
1.009347 0.00000393 0.00001744 0.00005076
1.014054 0.00000441 0.00001947 0.00005650
1.018782 0.00000505 0.00002222 0.00006424
1.023533 0.00000588 0.00002578 0.00007426
...略
可以把以上振動波函數隨距離變化的數據拷出來用Origin作圖。J=0時v=0,1,2的振動波函數曲線以及掃描得到的勢能曲線(紅線)如下所示(注:vibrot給出的這些振動波函數并沒有歸一化):
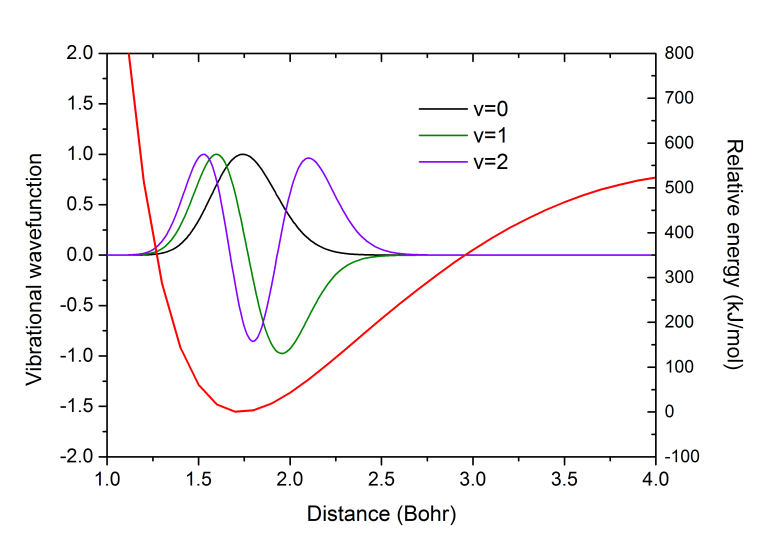
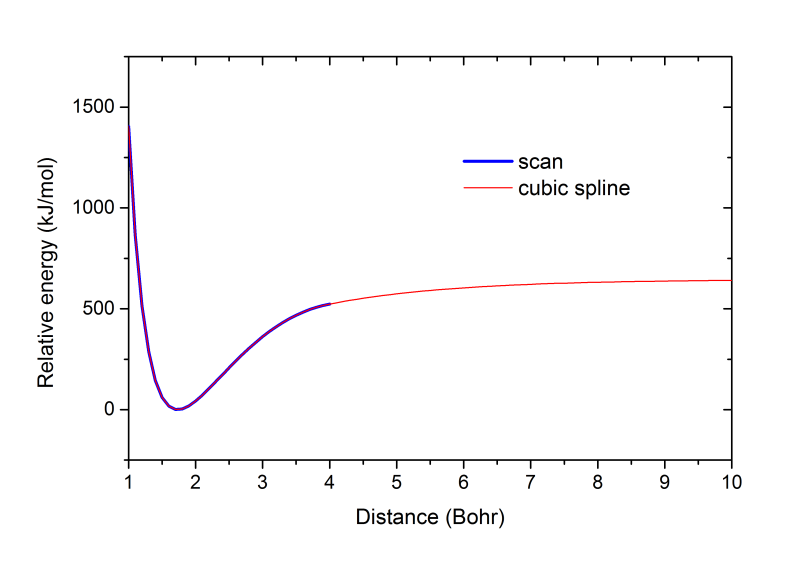
這里也把掃描得到的勢能曲線和輸出的vibHF.VibPlt0文件中包含的插值的勢能曲線放在一起進行比較。下圖藍線是掃描的1~4 Bohr范圍,紅線是插值出的1~10 Bohr范圍。可見vibrot做的插值是很合理的,很光滑,在1~4 Bohr內與掃描值吻合很好。
vibrot可以還可以給出各種振動平均的量,以及振動態間的躍遷屬性,簡單來說也就是能夠計算∫φ(v1)pφ(v2)dr,其中φ(v1)和φ(v2)是指某個轉動態的兩個振動波函數,程序直接算出來了,p是你感興趣的依賴于r的量,是你需要在observable字段中提供的。比如最簡單的情況,我們考察振動平均結構,就相當于計算∫|φ|^2 r dr,所以p就是坐標變量,我們要提供不同r位置時的距離值,其實就是在之前的輸入文件末尾加上下面這些,每個r位置的值正是r自己。
observable
1 1
1.1 1.1
1.2 1.2
1.3 1.3
1.4 1.4
1.5 1.5
1.6 1.6
1.7 1.7
1.8 1.8
1.9 1.9
2 2
2.1 2.1
2.2 2.2
2.3 2.3
2.4 2.4
2.5 2.5
2.6 2.6
2.7 2.7
2.8 2.8
2.9 2.9
3 3
3.1 3.1
3.2 3.2
3.3 3.3
3.4 3.4
3.5 3.5
3.6 3.6
3.7 3.7
3.8 3.8
3.9 3.9
4 4
此時輸出文件中多了一堆類似下面的內容,是每個J時各個振動態的對應于你給出的量的躍遷矩陣,這里只把J=0的貼出來
++ Matrix elements of observable: 1 1
>>>> matrix elements over vibrational wave functions (atomic units) for rotational quantum number 0
1 1 1.761059 2 1 -0.066339 2 2 1.847316 3 1 -0.005406 3 2 -0.094723 3 3 1.937822
observable
這里1 1、2 2、3 3對應的即是v=0、v=1、v=2的振動態的振動平均結構。而比如2 1對應的即是∫φ(v=2)rφ(v=1)dr的值,其實也正是兩個振動態之間的躍遷電偶極矩。由于當前不是諧振勢,因此可以違背諧振勢Δv=±1的旋律,因此3 1的值雖然遠比2 1的小但并不為0。
后面還輸出了下面的信息,是程序根據玻爾茲曼分布算出各個轉-振動態的分布比例,然后加權平均得到的特定溫度下的你所提供的量的平均值,對于當前來說就是溫度平均的鍵長。溫度可以在輸入文件里通過TEMPERATURE關鍵詞來設定。
Temperature averaged observable: 0.176187E+01 at 300.000K
本文介紹的內容,對于不研究雙原子分子光譜常數的人看似沒什么用,但實際上對于高精度計算雙原子分子熱力學相關數據是很重要的。比如計算雙原子分子的解離能,要考慮ZPE,本文的這種做法結合高級別勢能面掃描的數據得到的ZPE的結果是相當精確的。實際上也不用掃好幾十個點,只要在平衡位置上有一個點,附近再分布一些點(至少總共別少于7個),對于計算ZPE也夠了。而如果用比如Gaussian的freq=anharmonic關鍵詞來做非諧振計算試圖得到ZPE,那得算四階導數,而且對于CCSD(T)這樣連一階解析導數都沒有的方法更是根本不給算,明顯不適合高精度研究雙原子分子。而至于我們常用的基于諧振近似+ZPE校正因子的做法,對于精確研究雙原子分子的目的則顯然太糙了。