通過柔性力常數考察鍵的強度
1 關于鍵強的衡量
鍵的強度是化學研究者十分關心的問題。但鍵的強度不是一個確切的可觀測量,只是一個概念,具體衡量方式多種多樣,常見的有(1)鍵解離能(BDE)
(2)鍵級、AIM理論定義的BCP上的性質
(3)鍵長
(4)鍵方向上的力常數
其中,BDE定義為H(片段1)+H(片段2)-H(整體),這里H指焓,整體和片段結構都是分別優化的。BDE意義很明確,而且實驗可測,但它作為鍵強衡量標準也存在問題:
(1)結果依賴于片段的電子態的選取。這有一定任意性。比如乙烷斷裂成倆CH2,卡賓用單重態還是三重態對應的BDE結果是不同的。不過一般都是用片段的基態,以和實驗BDE相對應
(2)把片段的變形能給誤納入到對鍵強的衡量中去了。這里說的變形能是指片段從它在整個分子中的結構變化到孤立狀態下的結構過程的能量的變化。倒是也可以不優化片段來避免這個問題,但就不要用焓而要用電子能量了,此時結果和實驗BDE是沒法直接對應的(事實上,純理論方式研究鍵能一般就是用單點能相減,且不優化片段結構)
(3)很多體系很難拆分成合適的片段來只讓BDE反映感興趣的鍵的強度,環狀體系是典型。比如環丙烷,把一個C-C鍵充分拉開以打斷它勢必也導致其它變量產生顯著改變,因此能量變化不是對應單個C-C鍵的。廣義來說,對于兩個片段間存在多個鍵的時候,都很難計算出其中感興趣的鍵的BDE(雖然有時也可以設計一些特殊的計算路徑來估算出感興趣的鍵的BDE,但比較麻煩也有任意性)
相對于以上三點,BDE衡量鍵強度最大的弊端其實是:BDE反映的是整體和片段間的相對穩定性,這和單個鍵的強度原理上其實沒有必然關系。這點在DOI 10.1002/qua.25359一文章做了不錯的討論。舉一個例子:在CBS-QB3級別下計算二硅烯(就是把乙烯的碳換成硅,注意其極小點不是平面結構)的Si-Si鍵斷裂后變成兩個SiH2的過程,得到的標況下焓變是256.2 kJ/mol,而計算乙硅烷的Si-Si鍵斷裂變成兩個SiH3過程的焓變則是317.1 kJ/mol。可見BDE的結果明顯和實際鍵強沖突。二硅烯中Si-Si就算說不上是雙重鍵,但也肯定比乙硅烷的Si-Si單重鍵強,從鍵長上看前者也比后者明顯要短,但BDE順序卻是反過來的。此例BDE的失敗原因在于單重態SiH2過于穩定,導致二硅烯解離所需能量相對較小。
用鍵級能否衡量鍵強,這要看用的什么鍵級,諸如Mulliken鍵級爛得一塌糊涂。Mayer或Wiberg鍵級物理本質體現的是原子間共享的電子對數,對同類鍵(比如某個碳氧鍵與另一個碳氧鍵對比),它們與鍵強有一定正相關性,但完全沒法對不同類型鍵進行橫向對比。筆者提出的拉普拉斯鍵級與鍵強度有比Mayer/Wiberg鍵級明顯好得多的對應關系,但適用體系有局限性,主要用于有機體系。關于鍵級和鍵強更多的討論參閱拉普拉斯鍵級原文:J. Phys. Chem. A, 117, 3100 (2013)。對于同類鍵,AIM理論定義的BCP上的性質,如電子密度、勢能密度的絕對值等也與鍵強度有正相關性,但光靠BCP性質說事有時不靠譜,而且同樣沒法對不同類型鍵橫向比較。
拿鍵長討論鍵強度很常見,也很少受到質疑,而且是實驗可測的量,但也只能局限在同類鍵的比較上。
在很多文獻中對于同類鍵使用鍵的振動頻率來考察鍵的強度,上面的JPCA文章中也有例子。當使用諧振近似的時候,根據原子質量和振動頻率,可以直接解出鍵的力常數。當然,鍵的力常數也可以通過量子化學方法很容易地計算出來。簡單來說,鍵的力常數就是在鍵的平衡位置上,體系勢能對鍵長的二階導數(注:本文說的力常數一概沒有體現原子質量,坐標是非質權的),反映出在鍵方向上勢能面的曲率。曲率越大,則鍵伸縮單位長度時體系勢能提升得越多,反映出鍵的剛性越強,也可以因此認為鍵強越強。這點在觀念上很容易被接受,但注意鍵的剛性顯然不是鍵強度的唯一表征方式。用力常數衡量鍵強時可以在不同類型鍵之間橫向對比,而且不像BDE那樣需要以片段作為參考態,因而避免了任意性或不合理性。
對于雙原子分子,使用力常數討論鍵強很簡單,但到了多原子分子,由于內坐標或冗余內坐標的定義有任意性,坐標之間還有耦合,事情就比較麻煩了,直接從諸如Gaussian等量化程序頻率分析給出的Hessian矩陣中往往就沒法直接找到能較好反映鍵強的力常數項了。一個比較好的解決方法是Compliance matrix方法,下一節將對其進行介紹,更多的細節可以看綜述Chem. Soc. Rev., 37, 1558 (2008)
2 Compliance matrix方法的原理
要獲得鍵的力常數,最簡單的做法是直接取Hessian矩陣的對應的對角元。比如用Gaussian,使用內坐標方式書寫gjf里的坐標,然后在使用#P的情況下做freq任務,這時候在輸出文件中會看到Force constants in internal coordinates字段,這即是內坐標下的Hessian矩陣。假設輸入文件里4-1鍵對應第5個內坐標,那么在Hessian矩陣中找第5個對角元,就得到了4-1鍵的力常數。這種做法看似簡單卻有很大問題:(1)gview等程序自動生成的內坐標中往往沒有要研究的鍵,自己調整內坐標定義又比較麻煩。雖然自動產生的冗余內坐標對所有鄰近的原子都添加距離項,并且也可以自己隨意添加冗余內坐標,但是冗余內坐標下的Hessian矩陣有任意性,缺乏物理意義而沒法用,而且Gaussian也不輸出出來。
(2)Hessian依賴于內坐標的定義方式。例如對于H2O體系,考慮兩種內坐標定義,一種是用兩個H-O距離項和一個H-O-H角度項定義,另一種是用兩個H-O距離項和一個H-H距離項定義。在這兩種內坐標定義下O-H鍵的力常數是不同的,原因如下所示:
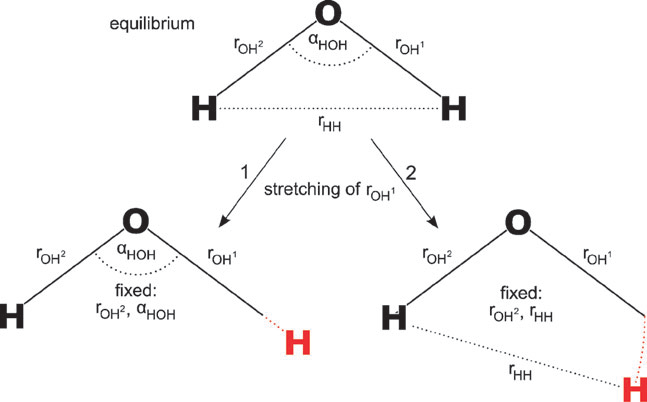
(3)直接使用Hessian對角元作為鍵的力常數等于忽略了變量間耦合的影響,這會導致其沒法定量準確反映鍵強(如后文所示,會高估力常數),甚至結論定性錯誤。比如下圖的例子,由于環張力,環丁烷的C-C鍵理應弱于丁烷C-C鍵,而直接用內坐標下的力常數不僅錯誤地判斷前者比后者強,還看到四個C-C鍵的數值沒有等價性,和點群對稱性不符。
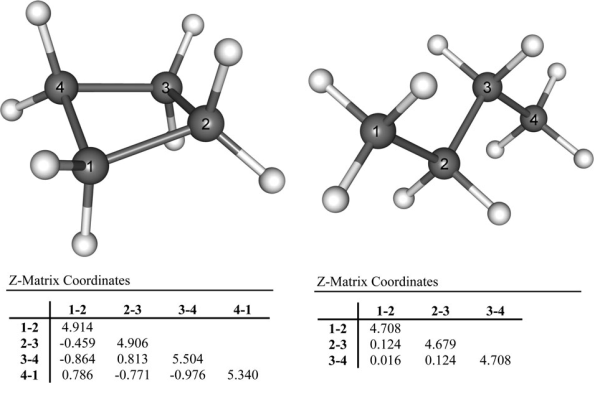
從上述三點,明顯知道直接用Hessian矩陣對角元作為鍵的力常數是不合適的。關于變量間的耦合,這里再多說一些。大家都知道剛性掃描(rigid scan)和柔性掃描(relaxed scan)的區別,剛性掃描時只有被掃描的變量發生改變,而柔性掃描時其它變量是允許自發弛豫到相應坐標方向上受力為0的位置的,明顯柔性掃描的勢能曲線更有實際意義,因為更符合真實情況,而剛性掃描的曲線只有理論意義。Hessian矩陣對角元實際上對應的是鍵的“剛性”力常數(rigid force constant),它相當于鍵長伸縮時不允許其它坐標弛豫情況下的力常數,相當于剛性掃描曲線的曲率;而真正能較好衡量鍵強的應當是“柔性”力常數(relaxed force constant),它對應鍵長伸縮時其它坐標可以自發弛豫情況下的力常數,相當于柔性掃描曲線的曲率。為了更直觀地說明這點,看下面的模型勢能面f(x,y)=x^2+y^2+x*y:
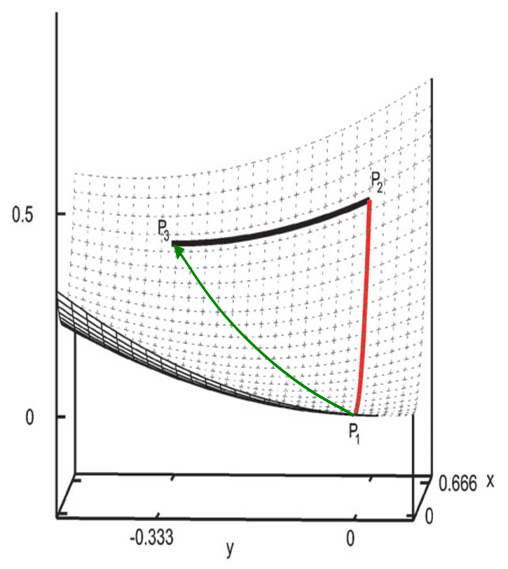
現在知道了,衡量鍵強要用柔性力常數。擬合力場參數的時候基本都是用的柔性掃描,然后再對勢能曲線擬合出力常數,這樣的力常數正是柔性力常數。但是這么來得到柔性力常數比較麻煩和耗時,掃描的每一步都相當于做一次限制性優化。
一種很方便、快捷的獲得柔性力常數的方法是compliance matrix方法。compliance matrix下面用C來表示,它的定義很簡單,就是Hessian矩陣的逆矩陣。位移列矢量Q和受力列矢量G可通過C聯系起來:Q=CG。根據這個關系,從C上引出兩個概念:
(1)Compliance constant:是C的對角元。第i對角元體現i坐標上受到一個單位的力時導致i坐標的位移,數值越小鍵越強
(2)Compliance coupling constant:是C的非對角元。(i,j)體現i坐標上受到一個單位力時j坐標的位移距離。這體現出變量在運動上的耦合
我們還是用前頭的模型勢能面f(x,y)=x^2+y^2+x*y來示例以便于理解。此體系的Hessian為
| 2 1 |
| 1 2 |
其逆矩陣,即C為
|2/3 -1/3|
|-1/3 2/3|
當體系x方向受力為1,y方向受力為0時,則對應的G為列矢量(1 0),將它右乘到C上,就得到位移列矢量Q=(2/3 -1/3),即x=2/3、y=-1/3。由于我們這里讓y方向受力為0,所以相當于在x方向位移的同時也在y方向充分弛豫。注意,x與y變量在勢函數中的耦合,體現在Hessian矩陣具有非零矩陣元上。如果勢函數中x與y沒有耦合,則Hessian為
| 2 0 |
| 0 2 |
其逆矩陣,即C為
|1/2 0 |
| 0 1/2|
利用此時對應的C再如上去計算G=(1 0)時所對應的Q,會發現x=1/2、y=0,即在x方向沒之前走得遠了。可見,勢函數中x與y存在耦合并且允許y坐標相應地發生弛豫,會明顯影響x受到單位力時所能移動的距離。為什么會這樣容易理解,因為存在耦合時x方向的受力為-2x-y,這是依賴于y坐標的,顯然y是否允許弛豫會影響x受到特定大小受力時能移動的幅度。所以,C矩陣中對應某個鍵的對角元能直接反映出在現實情況下(即其它幾何變量允許弛豫時)給這個鍵單位外力時它所能伸展的距離。(這里想再明確一下,Hessian的非對角元體現的是勢函數中變量間的耦合,它由此帶來C的非零對角元,表現出變量間在運動上的耦合)
在compliance matrix方法中,柔性力常數被直接定義為C矩陣對角元的倒數,搞懂了上面討論的C的對角元的物理意義,就自然而然知道這是為什么。
用C代替Hessian討論的優點還在于,C不依賴于內坐標的定義,并能夠保證等價的鍵對應的C對角元的等價性。對于使用冗余內坐標時,雖然C并非沒有任意性,但也有專門的方法可以合理構建它,可以將任意原子間距離項納入其中,從而直接考察任意原子之間的柔性力常數。另外,實際分子的C矩陣的非對角元相對于對角元通常較小,明顯小于Hessian的情況,因此對角元的物理意義也更為清楚。
利用C矩陣并進而得到柔性力常數是考察鍵強度的利器,在內坐標下實現很容易,就是求Hessian的倒數,但到了冗余內坐標下略麻煩,好在有現成的程序Compliance可以計算,用Gaussian(g03和g09經測試都兼容)做freq產生的fchk文件作為輸入即可,用起來很簡單。下面對其使用進行介紹。
3 Compliance程序的安裝
Compliance程序源代碼可以在http://www.oc.tu-bs.de/Grunenberg/compliance.html上免費下載。本文用的是撰文時最新的3.0.2版。Compliance只能在Linux下運行。編譯起來比較麻煩,主要是因為這是圖形程序,依賴于GTK庫,想編譯出來必須把庫文件都給找全了。雖然筆者很鄙夷Ubuntu,不過Ubuntu下倒是能把此程序所需要的庫都給弄齊,所以這里說在Ubuntu下怎么編譯。筆者用的是VMware下裝的Ubuntu 12。由于筆者的Ubuntu之前還裝過其它東西,所以不排除按照以下步驟安裝時還會提示缺一些東西,隨機應變即可。
在控制臺下運行
sudo apt-get install gcc
sudo apt-get install g++
sudo apt-get install gtkmm-2.4
sudo apt-get install libgtkglextmm-x11-1.2-0
sudo apt-get install libgtkglextmm-x11-1.2-dev
sudo apt-get install liblapack-dev
在software center里搜gmm,把libgmm++-dev裝上。
把Compliance壓縮包解壓,進入其中,運行
./configure
make
sudo make install
程序會被安裝到/usr/local/bin/compliance。運行compliance即可啟動。
4 Compliance程序的使用
compliance這個程序居然沒有自帶的幫助文件,怪哉!筆者也只能摸索著用,所以下面的功能介紹或許并不全面、嚴謹。啟動compliance后會看到圖形界面,在左上角選File - Open,在新窗口的右下角格式選.fchk,載入Gaussian做freq產生的.fchk文件,然后就會看到分子結構了。可以用右鍵上下拖動體系以縮放,用左鍵拖動來旋轉。
之后要做的事是添加感興趣的坐標,程序會把這些坐標對應的compliance matrix(C矩陣)顯示出來。compliance程序是主要用來考察鍵的,雖然也可以考察鍵角但貌似只是實驗性的,可靠性有限。在圖上點擊右鍵,可以看到有Stretching、Bending、Torsion三種模式。當處于Stretching(Bending)模式時,在圖上點擊兩個(三個)原子成為粉色,再點右鍵選Add/Remove coordinate,則這個鍵長(鍵角)項就會被添加。所有已添加的變量所構成的C矩陣會顯示在另一個窗口里。對于鍵長項單位是 埃/mdyn,要得到柔性力常數就把C矩陣對角元求倒數即可。至于Torsion模式選了也沒用,目前compliance程序并不支持考察扭轉項。
選中鍵長或鍵角后,也可以點擊右鍵后選Toggle animation,會播放這個坐標振動的動畫,連帶著其它坐標也會運動。估計就是把完整的C矩陣的相應的列作為了振動坐標來演示。
點擊C矩陣的列或行的標題,會把坐標對應的原子在圖形窗口中高亮為粉色,再次點擊標題可以播放動畫。
Edit菜單下有個Auto force adjust,似乎并不影響結果,只影響觀看動畫時候的振幅,關掉的話振幅可能比較離譜。
5 實例
5.1 乙酸
這里看一個簡單例子,乙酸。用# B3LYP/6-31G* opt freq關鍵詞計算,把chk轉換成fchk文件(如果是Windows版,轉化出來是fch,后綴自行改成fchk即可),然后載入Compliance程序。把乙酸中O-H、C-O、C=O、C-C、C-H(三個C-H特征相近,只需加入一個)都加入。如果只需要研究其中的某些鍵,可以只加入相應的,加入多少不會影響C矩陣數值,只不過沒加入的不會顯示而已。當前C矩陣如下
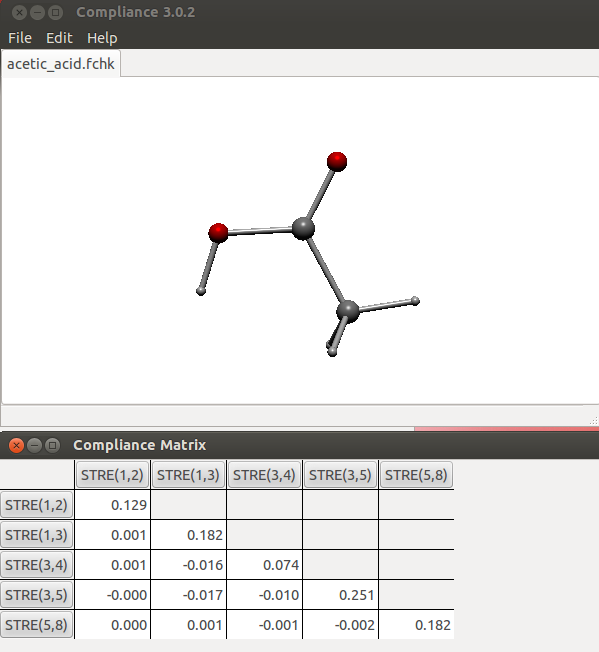
此程序不好之處是顯示不了原子標簽,所以給出下圖以便對照
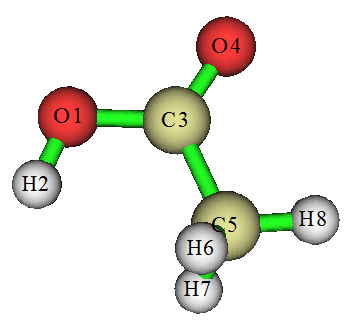
在當前C矩陣中,對角元數值越小說明對應的鍵強度越大。為了對比更方便,我們把這些對角元取倒數得到柔性力常數(mdyn/埃):
O-H:7.75
C-O:5.49
C=O:13.51
C-C:3.98
C-H:5.49
從數值上,可看到C=O比C-O明顯要強,這很合乎化學直覺。原理上柔性力常數是可以對不同類型鍵來橫向比較鍵強度的,所以從上述數值中也能了解不同類型鍵的相對強度。雖然可能有些和化學直覺以及BDE值不符,比如從數值上看O-H比C-C強不少,有點難以從常識上理解,但由于鍵強也沒有唯一標準去衡量,所以也沒法說結果不合理。
5.2 順鉑(順式二氯二胺合鉑)
順鉑里面有Pt-N和Pt-Cl兩種配位鍵,我們嘗試用柔性力常數看看哪個配位鍵強度更大。用B3LYP泛函,對Pt用SDD,其余的用6-311G*,所得C矩陣如下,其中1-2、1-3對應Pt-Cl鍵,1-4、1-5對應Pt-N鍵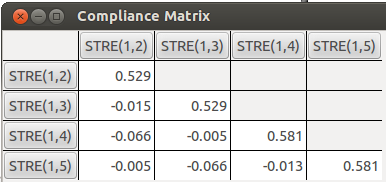
5.3 GC堿基對
下面來看鳥嘌呤(G)和胞嘧啶(C)形成的氫鍵二聚體。在M062X/6-311G**級別下優化并算了頻率,然后用Multiwfn做了AIM分析,如下所示,圖中桔黃色的點是鍵臨界點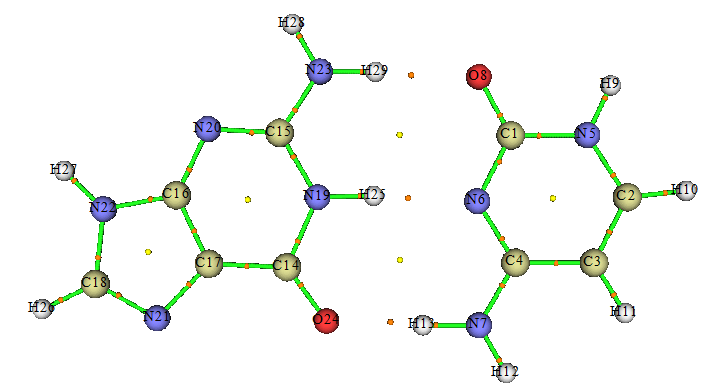
在Chem. Phys. Lett., 285, 170 (1998)中,Espinosa等人提出對于X-H...O (X=C,N,O)型氫鍵可以用H...O間臨界點的勢能密度絕對值的二分之一作為氫鍵鍵能。根據筆者的經驗,這個關系確實比較準確。G、C之間有兩個N-H...O氫鍵和一個N-H...N氫鍵,雖然并沒有證據表明Espinosa的關系也能較好用于N-H...N型氫鍵,但我們還是試圖使用這個關系來對比這三個氫鍵的強度。通過Multiwfn可以得到鍵臨界點上的勢能密度,根據Espinosa方法估計出來的氫鍵強度為:
N23-H29...O8:27.8 kJ/mol
N19-H25...N6:33.5 kJ/mol
O24...H13-N7:43.1 kJ/mol
我們再來看看氫鍵中涉及到的兩個H...O和一個H...N構成的C矩陣
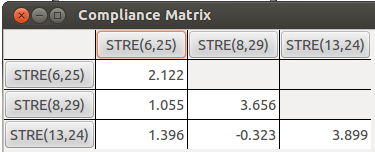
對應的柔性力常數為(給出的是氫原子和氫鍵受體間的值):
N23-H29...O8:0.273
N19-H25...N6:0.471
O24...H13-N7:0.256
可見弱相互作用對應的柔性力常數明顯小于化學鍵,比乙酸例子中的值小了一個數量級左右(典型化學鍵與氫鍵的BDE的比例也和這個差不多)。
對當前體系,不幸的是,勢能密度估算的氫鍵鍵能和柔性力常數并沒有正相關性,甚至對于兩個相同類型的N-H...O氫鍵,兩種方法給出的強度關系都是反著的。再看氫鍵距離,H29...O8的距離是1.902埃,而O24...H13距離是1.768埃,明顯后者應當比前者強,但柔性力常數卻是前者比后者大,因此對此例若通過柔性力常數判斷氫鍵強度明顯就被誤導了(雖然Chem. Soc. Rev.文章圖7里面兩個氫鍵強弱關系是對的,但沒道理M062X/6-311G**這么適合優化氫鍵的級別結果卻不對,所以還是分析方法的問題)。另外,N19-H25...N6的柔性力常數顯著大于另兩者,若說它的強度明顯更大也沒法解釋得通。
為什么compliance matrix方法判斷這個體系氫鍵強度這么爛,會明顯造成誤判,在Compliance程序里播放一下三個氫鍵對應的振動動畫就容易理解了(實際上也對應于對三個氫鍵做柔性掃描的軌跡)。中間那個氫鍵在伸縮時會連帶著旁邊兩個氫鍵一起伸縮(因為允許其它坐標的弛豫),確實我們從C矩陣的第一列非對角元上也可以看到它與另外兩個氫鍵在運動上的耦合很大,因此它運動起來費勁,體現為柔性力常數比較大。而兩邊的氫鍵,播放動畫時會看到它的伸縮也會明顯牽動中間氫鍵發生伸縮,但另一頭的氫鍵不怎么動,因此運動所受阻礙相對較小,體現出的柔性力常數就沒那么大了。這里可見,雖然柔性力常數總是有物理意義的,但也并不是說什么時候都能和鍵的強度對應起來。
當前這個例子絕對不是說柔性力常數不適合衡量弱相互作用強度,而是說,對于一些特殊情況應當結合動畫予以恰當的解釋,不能盲目地從數值上討論鍵強。如果某個坐標和其它坐標對應的C矩陣的非對角元(即Compliance coupling constant)比較小,那么相應的對角元(Compliance constant)是可以較好衡量這個坐標的剛性的;如果這個坐標對應鍵,則可以用來討論鍵的強度。