使用NWChem做分數占據數的DFT計算
1 前言
分數占據數(Fractional occupation number, FON)計算是指被計算的體系有的軌道占據數不為整數,也因此允許整個體系的電子數不為整數。這看似有點超現實,實際中體系電子數不可能為非整數,畢竟電子不可分割,但對于DFT(或HF)計算是可以實現的,而且在程序實現上超簡單。大家知道,常規DFT計算的時候都是已知電子數,根據每一輪迭代時解出的KS軌道能量從低往高填充,然后用占據軌道構建用于下一輪迭代用的密度矩陣以及計算體系能量。而FON計算時,有的軌道依然是整數占據,有的則是自設的分數占據數(這有點像自然軌道),構建密度矩陣時考慮所有這些占據數不為0的軌道即可,除此以外不需要對程序做任何修改。FON計算既可以是限制性計算,軌道占據數允許在[0,2]范圍,也可以是非限制性計算,alpha/beta軌道占據數允許在[0,1]范圍。做FON計算有一些特別的用處,很重要之一就是考察各種近似的交換-相關泛函存在的自相互作用誤差(self-interaction error, SIE)導致的離域性誤差(delocalization error)問題。這里引用doi: 10.3866/PKU.WHXB201605301中的一張圖,圖中ΔN指相對于中性狀態時電子數的改變,縱坐標是相對于中性狀態時體系能量的變化。
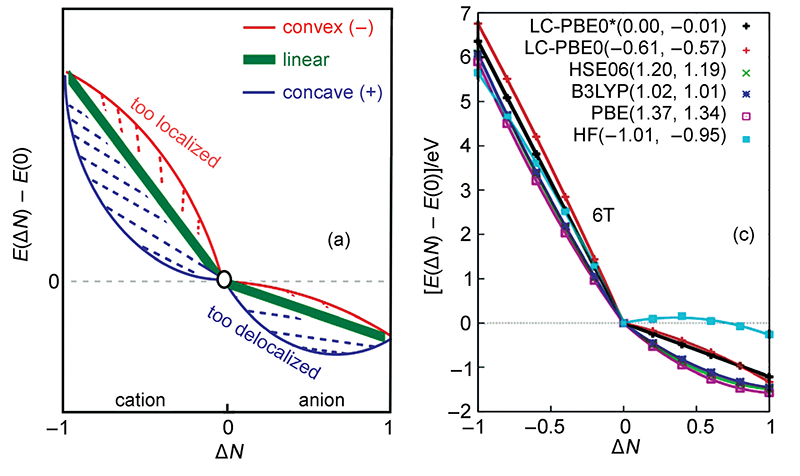
理論上,如果交換-相關泛函是精確,那么體系能量隨電子數的變化應當如圖中綠線所示,是精確的折線。但是HF成份較低的泛函存在較大的SIE問題,導致電子離域性過強,所以從右圖上可看到PBE、B3LYP等泛函的曲線都往外凸,而且HF成份越低凸得越厲害。HF交換勢則完全沒有SIE問題,但是在圖中看到其曲線往里凹,高估了電子定域性,也不很合理。近年來比較火的w調控方法則可以對范圍分離泛函的HF交換勢摻入的方式優化到一個較理想的情形,它使得HOMO軌道能量和體系電離能盡可能接近(對于精確泛函二者則嚴格相同),從而極大程度解決SIE問題,使得對超極化率、中/大體系激發能等方面精度提升很多,圖中可見經過w調控的泛函LC-PBE0*的曲線確實相當平直。更多和w調控的討論見《優化長程校正泛函w參數的簡便工具optDFTw》(http://www.shanxitv.org/346)。
如今大量使用w調控的文章都紛紛繪制如上的圖像討論不同泛函的SIE,本文就介紹怎么在NWChem中做FON計算并繪制如上的圖像。
2 在NWChem中做分數占據數計算
NWChem是為數不多的能支持FON計算的量化程序,開源免費。編譯方法參看《NWChem 6.6編譯方法》(http://www.shanxitv.org/270)。NWChem中支持分數占據數的DFT計算。不是光指定一個總電子數就完了,而必須在DFT段落中用fon關鍵詞來指定占據方式。下面的語句是個用于閉殼層FON計算的設定例子:
fon partial 2 electrons 0.8 filled 5
代表有兩個軌道是分數占據的,0.8個電子均分給這兩個軌道。另外有5個雙占據軌道。因此此體系一共有0.8+5*2=10.8個電子。
對于開殼層體系,需要分別對alpha和beta軌道定義占據數,比如
fon alpha partial 2 electrons 0.8 filled 6
fon beta partial 1 electrons 1 filled 5
ODFT
這代表有6個占據數為1.0的alpha軌道,另有0.8個電子均分給兩個alpha軌道。占據的beta軌道有6個,占據數都為1.0(含義上等價于fon beta partial 0 electrons 0 filled 6,但不能這么寫否則程序報錯)。ODFT必須寫,指明做開殼層DFT計算(O代表Open)。
在NWChem中普通的計算都是通過charge關鍵詞指定體系凈電荷以及在DFT字段中用mult關鍵詞指定自旋多重度來讓程序知道電子是怎么排布的。而做FON的時候我們是自行指定電子排布方式的,因此不需要再寫charge和mult了。
3 對吡咯做分數占據數計算
這里我們對吡咯體系做FON計算。吡咯總共36個電子,因此中性狀態下alpha和beta軌道各有18個占據軌道。假設我們當前研究體系有36.7個電子的情形,則多出來的0.7個電子應當被視為處在一個alpha軌道上(可以姑且視作是處在中性狀態下的alpha LUMO軌道上,但注意36.7個電子計算和36個電子計算得到的軌道形狀和能量都是不同的)。B3LYP/6-31G*時輸入文件如下,結構是事先在B3LYP/6-31G*下對中性狀態優化的。GEOMETRY
C 0.00000000 1.12552000 0.33154500
C 0.00000000 0.71275300 -0.98347600
C 0.00000000 -0.71275300 -0.98347600
C 0.00000000 -1.12552000 0.33154500
N 0.00000000 0.00000000 1.12233100
H 0.00000000 0.00000000 2.13032900
H 0.00000000 2.11411400 0.76778100
H 0.00000000 1.36093100 -1.84951800
H 0.00000000 -1.36093100 -1.84951800
H 0.00000000 -2.11411400 0.76778100
END
BASIS
* library 6-31G*
END
DFT
fon alpha partial 1 electrons 0.7 filled 18
fon beta partial 1 electrons 1 filled 17
odft
XC b3lyp
END
TASK DFT ENERGY
輸出信息和普通單點計算沒什么區別,計算速度和普通單點計算也沒什么差異,有個別地方值得說一下。以下是迭代過程中隨便取的一部分
FON applied
tr(P*S): 0.3670000E+02
d= 0,ls=0.0,diis 5 -210.0871635921 -3.83D-04 1.03D-04 6.20D-05 3.8
5.87D-05 3.40D-05
這里tr(P*S)后面的值對應的是當前體系電子數,由于密度矩陣是按照自設的分數占據方式構建的,當前這里顯示有36.7個電子。
然后值得說的是輸出的軌道信息部分,從alpha軌道部分可以看到,前18個軌道占據數都是1.0,從20號軌道開始占據數都是0,而第19號軌道,占據數是我們設的0.7:
Vector 19 Occ=7.000000D-01 E= 1.739512D-01 Symmetry=b1
再看beta軌道部分,會看到前18個都是1.0占據,其余的都是0占據。
有興趣的話可以通過FON計算體系凈電荷為-1、0、+1狀態的能量,和我們通過常規UKS方式計算的結果進行對比。你會發現,當電子數為整數的時候,兩種方式結果是完全一樣的。比如吡咯體系凈電荷為+1時設定為
fon alpha partial 1 electrons 1 filled 17
fon beta partial 1 electrons 1 filled 16
odft
結果為-209.872709779915(這里我們令alpha電子數>beta電子數是習俗。若設成alpha電子數為17,beta為18,則結果也一樣)。直接用charge 1結合mult 2做常規UKS計算,結果為-209.872709372573,可見和FON計算一樣(微小的數值差異可以忽略)。
4 對吡咯體系考察不同泛函的離域性誤差
下面我們在B3LYP/6-31+G*級別下對吡咯計算和繪制能量隨電子數的變化,以考察不同泛函的離域性誤差。考慮的電子數變化區間是ΔN=[-1,1],步長是0.1。雖然可以直接手動去不斷地改輸入文件并計算各個電子數時候的能量,但是這樣太費事。為了省事,我們通過shell腳本自動完成。這里提供兩個腳本,一個是run1.sh,用來掃描ΔN=[-1,0)區間,另一個是run2.sh,用來掃描ΔN=[0,1]區間。
以下是run1.sh,將其內容復制到一個文本文件里,用chmod加上可執行權限,然后用./run1.sh,則這個腳本就會不斷地改變FON設定并產生NWChem輸入文件input.nw,并調用NWChem自動執行之。任務會依次產生n1.0.out、n0.9.out ... n0.1out,對應于ΔN從-1.0變化到0.1
for ((i=0;i<10;i=i+1))
do
chg=`echo "$i*0.1"|bc`
chgtmp=`echo "1.0-$i*0.1"|bc`
file=n`printf "%4.2f\n" $chgtmp`
echo processing $file...
cat << EOF > input.nw
GEOMETRY
C 0.00000000 1.12552000 0.33154500
C 0.00000000 0.71275300 -0.98347600
C 0.00000000 -0.71275300 -0.98347600
C 0.00000000 -1.12552000 0.33154500
N 0.00000000 0.00000000 1.12233100
H 0.00000000 0.00000000 2.13032900
H 0.00000000 2.11411400 0.76778100
H 0.00000000 1.36093100 -1.84951800
H 0.00000000 -1.36093100 -1.84951800
H 0.00000000 -2.11411400 0.76778100
END
BASIS
* library 6-31+G*
END
DFT
fon alpha partial 1 electrons 1 filled 17
fon beta partial 1 electrons $chg filled 17
odft
XC b3lyp
END
TASK DFT ENERGY
EOF
nwchem input.nw > $file.out
done
以下是run2.sh,運行方式同上。任務會產生0.0.out、n0.1.out ... 1.0.out文件,對應ΔN從0.0變化到1.0。
for ((i=0;i<=10;i=i+1))
do
chg=`echo "$i*0.1"|bc`
file=`printf "%4.2f\n" $chg`
echo processing $file...
cat << EOF > input.nw
GEOMETRY
C 0.00000000 1.12552000 0.33154500
C 0.00000000 0.71275300 -0.98347600
C 0.00000000 -0.71275300 -0.98347600
C 0.00000000 -1.12552000 0.33154500
N 0.00000000 0.00000000 1.12233100
H 0.00000000 0.00000000 2.13032900
H 0.00000000 2.11411400 0.76778100
H 0.00000000 1.36093100 -1.84951800
H 0.00000000 -1.36093100 -1.84951800
H 0.00000000 -2.11411400 0.76778100
END
BASIS
* library 6-31+G*
END
DFT
fon alpha partial 1 electrons $chg filled 18
fon beta partial 1 electrons 1 filled 17
odft
XC b3lyp
END
TASK DFT ENERGY
EOF
nwchem input.nw > $file.out
done
執行以上兩個腳本,都算完了之后,運行grep "Total DFT energy" *.out,就會把能量從所有的輸出文件中提出來。把內容拷到文本文件里,再用ultraedit之類工具改成如下這樣格式:
0.00 -210.177778579314
0.10 -210.177659716794
0.20 -210.176820011604
0.30 -210.175152111372
0.40 -210.172599674556
0.50 -210.169127332116
0.60 -210.164712722296
0.70 -210.159342627221
0.80 -210.153010888050
0.90 -210.145717291579
1.00 -210.137466938372
-0.10 -210.155373098208
-0.20 -210.131259526415
-0.30 -210.105428293496
-0.40 -210.077870858885
-0.50 -210.048579636682
-0.60 -210.017547727497
-0.70 -209.984769772638
-0.80 -209.950240400890
-0.90 -209.913955349549
-1.00 -209.875911118025
然后把此文件拖到Origin里,會被導入成列兩數據,在第一列標題上點右鍵選Sort Worksheet - Ascending對ΔN排序。然后做成折線+散點圖,如下所示
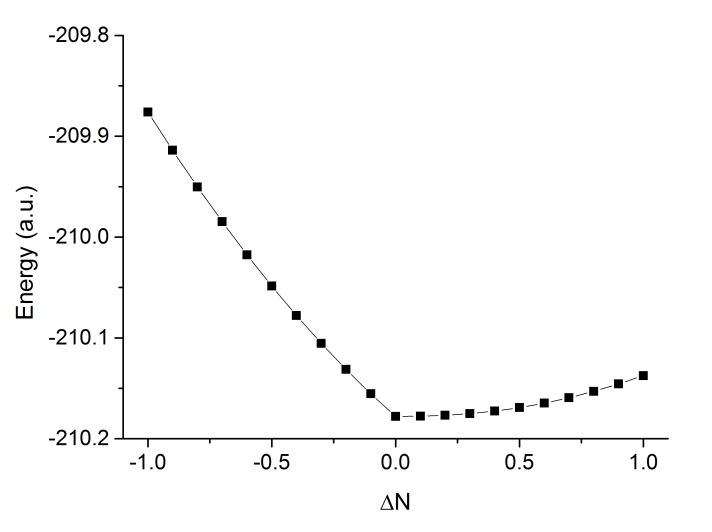
可見中性狀態能量最低,得電子也會導致能量上升,電子親和能為負。
接下來我們把其它泛函的結果計算出來作到同一張圖上來對比。我們考察HF、M06-2X、PBE,把腳本中的b3lyp分別改為HFexch、m06-2x、xpbe96 cpbe96然后重新運行腳本即可。由于每種泛函得到的絕對能量有系統性偏差,為了作在一張圖上好比,我們把每個泛函不同電子數時的能量都減去這個泛函在ΔN=0時的能量,使得四個泛函的曲線在ΔN=0處重合。最后作出的圖如下:
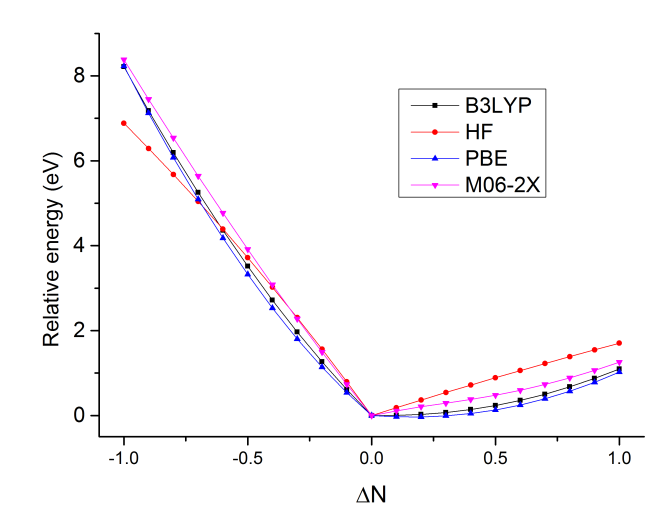
可見HF成份越低的泛函,尤其是純泛函,曲線往外凸得越厲害,說明SIE問題越大。M06-2X的曲線相對比較直,SIE問題不顯著,但這不代表M06-2X對其它體系曲線也能這么直。HF則在左半邊的圖中往里凹了,說明高估了電子定域性。
下面我們來看看使用如今熱門的w調控方法得到的泛函結果如何。我們對LC-wPBE泛函在6-31+G*下計算最優的w值,使用optDFTw程序來實現非常容易,詳見《優化長程校正泛函w參數的簡便工具optDFTw》(http://www.shanxitv.org/346)。最后得到的最優的w值為0.300047。
在NWChem中,LC-wPBE在調用的時候是在DFT字段里寫如下內容(手冊里是這么寫的,但實際上標準的LC-wPBE的w參數應為0.4)
direct (對于范圍分離泛函必須寫direct)
xc xwpbe 1.00 cpbe96 1.0 hfexch 1.00
cam 0.3 cam_alpha 0.00 cam_beta 1.00
其中cam就是w參數,cam_alpha和cam_beta就是分別對應范圍分離泛函的alpha和beta參數。我們下面要使用經過w調控的LC-wPBE對ΔN進行掃描,于是把run1.sh和run2.sh中XC b3lyp替換以下內容
direct
xc xwpbe 1.00 cpbe96 1.0 hfexch 1.00
cam 0.300047 cam_alpha 0.00 cam_beta 1.00
然后運行這兩個腳本。對比其它泛函會發現范圍分離泛函在NWChem中速度賊慢,而在Gaussian中則要好得多。
將結果作圖,如下所示
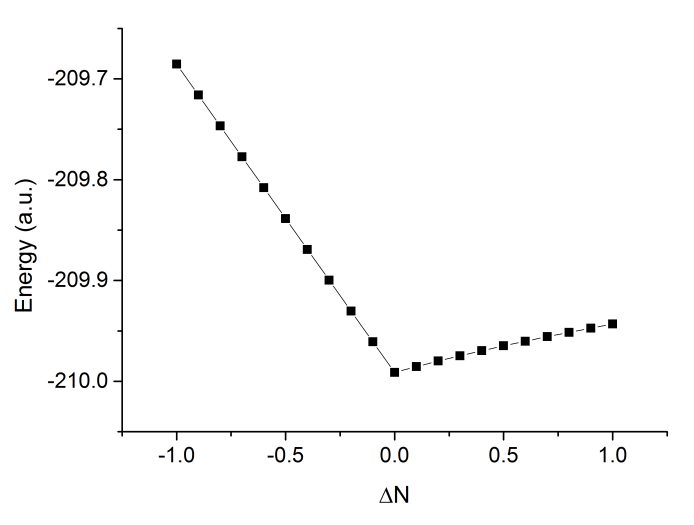
可以看到曲線明顯非常直,說明w調控是有效的削弱SIE問題的方法。
5 計算p軌道占據數平均化的碳原子
前面我們看到的是只有一個軌道是分數占據的計算,下面我們看個多個軌道都是分數占據的例子。眾所周知碳原子基態組態是s2p2,占據的兩個p軌道和沒被占據的p軌道的軌道能量是不同的,體系的電子密度也不是球對稱分布的。但是三個p軌道在原理上是等價的,在現實中觀測到的碳原子密度也是球對稱的。如果我們做FON計算,就可以還原這種情況,輸入文件如下,我們令體系中2個電子平均地攤在三個p型alpha軌道上,而alpha和beta s軌道的電子占據方式則不變。GEOMETRY
C 0. 0. 0.
END
BASIS
* library 6-31G*
END
DFT
fon alpha partial 3 electrons 2 filled 2
fon beta partial 1 electrons 1 filled 1
odft
XC b3lyp
END
TASK DFT ENERGY
從輸出文件中可看到如下信息。確實,三個占據數為2/3的alpha p軌道的軌道能量是相同的,衡量徑向延展廣度的r^2算符的期望值也是相同的
Vector 3 Occ=6.666667D-01 E=-2.232569D-01
MO Center= -6.4D-17, -1.0D-17, -8.4D-17, r^2= 9.8D-01
...略
Vector 4 Occ=6.666667D-01 E=-2.232504D-01
MO Center= -2.8D-16, -6.2D-17, 1.6D-16, r^2= 9.8D-01
...略
Vector 5 Occ=6.666667D-01 E=-2.232504D-01
MO Center= 7.7D-16, 1.5D-16, 2.8D-16, r^2= 9.8D-01
...略
總能量為-37.808815282934。
如果做常規的UKS計算,設mult 3,則對應的三個alpha p軌道信息為
Vector 3 Occ=1.000000D+00 E=-2.527187D-01
MO Center= 9.5D-17, 4.7D-16, -1.0D-15, r^2= 9.6D-01
...略
Vector 4 Occ=1.000000D+00 E=-2.527186D-01
MO Center= 6.2D-16, -4.9D-16, -5.5D-16, r^2= 9.6D-01
...略
Vector 5 Occ=0.000000D+00 E=-1.388507D-01
MO Center= 5.3D-16, 1.8D-15, 3.5D-15, r^2= 1.1D+00
...略
明顯,沒占據的p軌道能量顯著高于占據的p軌道,而且從r^2上看,其延展程度也更高。總能量為-37.846279559548,比FON計算時略低,根據變分原理這是更優的解,所以要得到碳的真實基態能量還是得做常規UKS計算。而至于實際中為什么觀測到的碳原子的密度是球對稱的,應理解為其真實的密度矩陣是不同p軌道占據方式對應的密度矩陣的線性疊加,牽扯到系綜密度矩陣的概念了,這里就不多說了。