簡談NBO間的相對相位問題

簡談NBO間的相對相位問題

文/Sobereva @北京科音  2013-Jun-13

在思想家公社群里有人研究C2H5OC2H5自由基陽離子，問為何在6-31+G*和6-31++G**下得到的beta NBO中的氧的LP*與C-H的BD的相對相位發生了反轉、這樣情況下如何討論軌道間相互作用。這個問題感覺還是值得專門談一下的。

這個相位反轉問題如下圖所示。綠色/藍色代表O LP*的正/負相位。黃綠/紫色代表C-H BD。可見O LP*的相位在兩種情況下恰好相反。

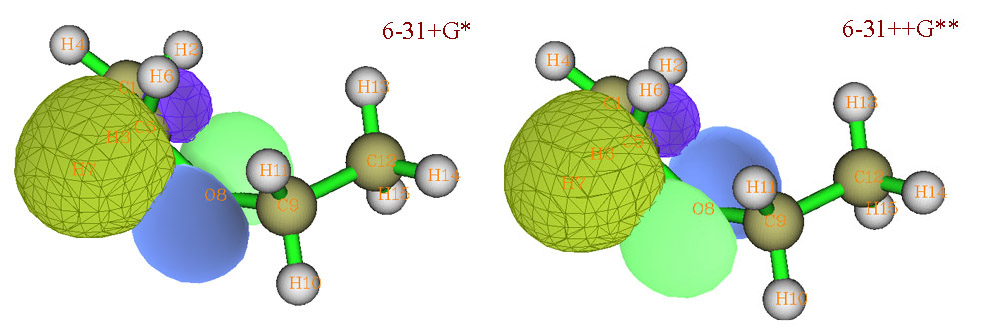
NBO（也包括PNBO）的相位是有隨機性的。因為獲得NBO的過程是對每個原子自身，以及每兩個原子間構成的以NAO為基的密度矩陣進行對角化而產生的。而不是像自然軌道那樣對整個體系的密度矩陣對角化而得到的。每次對角化后產生的一批NBO之間的相對相位是固定的不變的，但是這批NBO的相位可以同時反轉（即全部本征矢變為其負本征矢），而不影響物理意義，因為這不會使本征值（NBO占據數）因此發生改變。

由于不是來自同一個中心或同一個原子對兒的兩個NBO不是在同一次對角化過程中產生的，所以二者的相對相位是隨機的。

以C-H為例，C-H的BD，即便兩次計算時基組、構型、理論方法相差甚微，也可能有的時候BD中正相位占主導，而在另一種情況下BD的相位就反轉了而負值占主導。對角化算法只保證對于一個矩陣得到的本征值是確定的，而本征矢可以隨意乘上一個常數（如-1）。然而，同一個C-H的BD和BD*是在同一次對角化時產生的，所以此二者間的相對相位則是絕對不變的，要反轉其中一個就必須反轉另一個。

實際上寡人在開發Multiwfn (http://www.shanxitv.org/multiwfn)的AdNDP功能時也遇到過類似問題。AdNDP軌道是對于不同的單、雙或多中心的密度矩陣對角化產生的，為了使相位看起來統一從而比較方便，Multiwfn在輸出AdNDP軌道的格點數據的時候，當發現如果軌道負值區域占主導，那么就給軌道系數都乘上-1來讓它反轉，使得所有AdNDP軌道都是以正相位為主。其實NBO程序也應該加入這么一個自動檢測并自動反轉相位的功能。不過，對于LP、pi軌道，正負值區域都相同，就無法靠這種辦法調整相位了，但也依然可以有辦法讓相位唯一地確定下來，比如可以積分z*psi(x,y,z)，比如結果為負，那么表明軌道負相位的一頭沖著z軸正方向，此時就可以令之相位反轉。

所以，上面所看到的在6-31++G**下相對于6-31+G*時，beta NBO中O LP*和C-H BD的相對相位發生了反轉，這沒有關系，不影響物理意義。作這種圖，只能考察它們之間重疊程度，由此來估量相互作用是否可能比較大或比較小，或者來解釋E2值。在O與C-H之間交匯區域內，在6-31++G**和6-31+G*時，兩個NBO的重疊程度是一致的，只不過重疊積分符號顛倒了而已。單純的這種顛倒并不影響這兩個NBO間的二階穩定化能(E2)值，而E2正是兩個NBO對應的軌道間的相互作用的定量衡量標準。B3LYP結合6-31+G*和6-31++G**下這兩個NBO間的E2分別為13.13kcal/mol和13.39kcal/mol，可見相差甚微。

值得一提的是：NBO之間全都是正交的，整個空間內重疊積分為0，上面只說O與C-H之間交匯區域內的情況。考察這種軌道重疊問題用PNBO比用NBO更好，因為PNBO不要求軌道間正交，所以可以更好地展現軌道間的重疊。不過當觀看軌道時的isovalue不太小時，NBO和PNBO看起來差異往往不大，此時也能通過NBO考察軌道間的重疊。

NBO和PNBO的差異如下圖所示

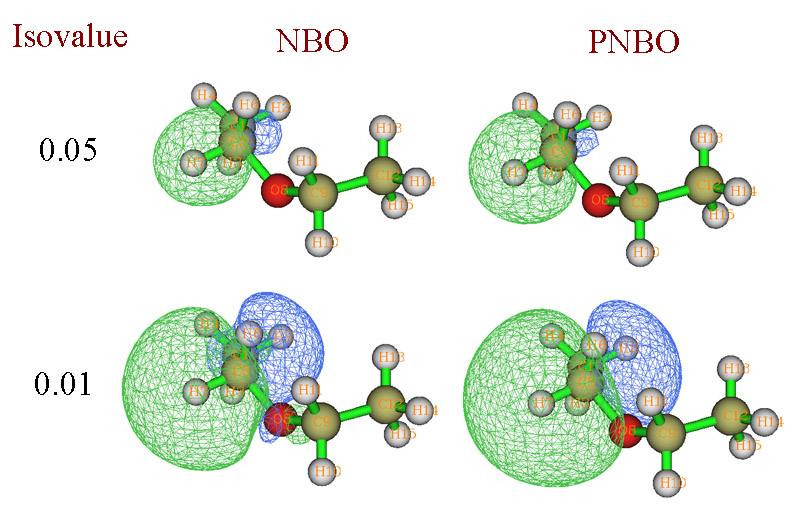
可見，isovalue=0.05時，NBO和PNBO都如實展現了C-H成鍵軌道的特征。然而當isovalue=0.01時，NBO的圖形就變得復雜了，不僅軌道變了形，在相鄰原子上還出現了小等值面，因為若不具備這樣的特征，就沒法和周圍的NBO正交了。而PNBO則依然很好地展現出C-H成鍵軌道的特征。