在球面上隨機均勻分布點的算法

寫個程序時遇到一個問題，需要得到在一個單位球面上隨機分布一批點的坐標，想了想辦法，第一個辦法是選取一個起始點(1,0,0)，然后依次繞著X、Y、Z軸隨機旋轉一定的角度，Fortran代碼如下
x=1
y=0
z=0
!Step 1: Rotate about Z axis
call RANDOM_NUMBER(rotval)
rotval=rotval*2*pi
xtmp=cos(rotval)*x-sin(rotval)*y
ytmp=sin(rotval)*x+cos(rotval)*y
x=xtmp
y=ytmp
!Step 2: Rotate about Y axis
call RANDOM_NUMBER(rotval)
rotval=rotval*2*pi
xtmp=cos(rotval)*x-sin(rotval)*z
ztmp=sin(rotval)*x+cos(rotval)*z
x=xtmp
z=ztmp
!Step 3: Rotate about X axis
call RANDOM_NUMBER(rotval)
rotval=rotval*2*pi
ytmp=cos(rotval)*y-sin(rotval)*z
ztmp=sin(rotval)*y+cos(rotval)*z
y=ytmp
z=ztmp

點不是很多的話，看起來還蠻均勻，能用，但點數多了就會發現點的分布并不均勻，100000個點時如下所示，可以隱約看到有一個環狀分布比較密集。



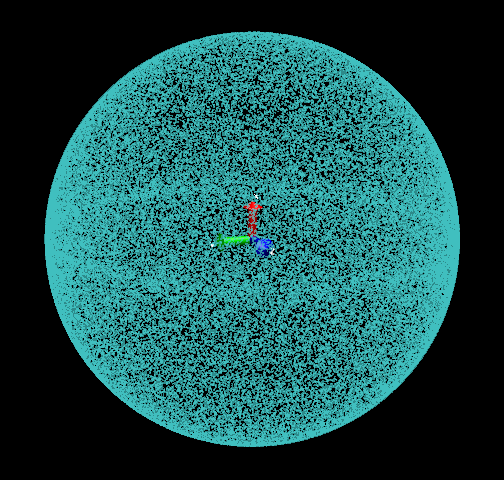
出現此問題的原因是，雖然第一步得到了一個均勻隨機的環狀分布，但是第二步的時候在球的兩極已經有點的聚集現象了，第三步時把這個問題弱化了，但是聚集的兩極經過繞著X軸轉一圈后，還是略微形成了環狀密集分布區域。


感覺不夠完美，又在網上找找有沒有什么其它方法，看到一個做法，對應的Fortran代碼：
call RANDOM_NUMBER(rotval)
theta = pi*rotval
call RANDOM_NUMBER(rotval)
phi = 2*pi*rotval
x=sin(theta)*cos(phi)
y=sin(theta)*sin(phi)
z=cos(theta)
試了下，發現很坑爹，點在兩極嚴重聚集。給出這樣算法的人真是不負責任，10000個點時分布如下所示




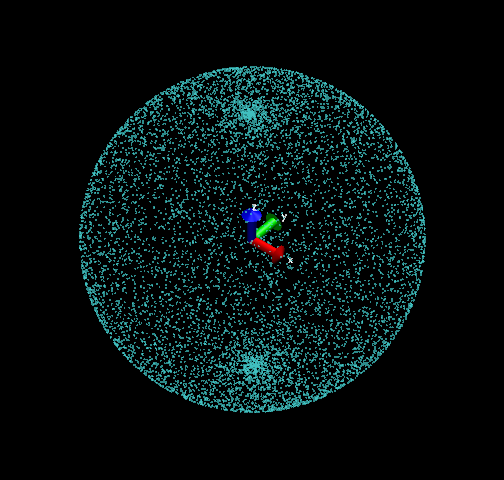
于是搜英文資料，發現一個頁面很好，http://mathworld.wolfram.com/SpherePointPicking.html，專門介紹了獲得球面上隨機分布點的算法，沒想到還專門有算法解決這個問題。其中最簡單實用的Marsaglia的方法，非常好。過程是，在(-1,1)區間內隨機取兩個值x1和x2，若這兩個值的平方和大于等于1則重新選取。然后球面上的點的x、y、z的坐標用x1和x2就可以很簡單得到，Fortran代碼如下
do while(.true.)
    call RANDOM_NUMBER(x1)
    call RANDOM_NUMBER(x2)
    x1=2*(x1-0.5D0)
    x2=2*(x2-0.5D0)
    if (x1**2+x2**2<1) exit
end do
x=2*x1*dsqrt(1-x1**2-x2**2)
y=2*x2*dsqrt(1-x1**2-x2**2)
z=1-2*(x1**2+x2**2)

10000個點的時候分布如下，非常均勻完美