繪制躍遷密度矩陣平面圖分析電子躍遷
重要提示:此文已經完全過時了,不要再看。讀者務必看筆者后來寫的《使用Multiwfn繪制躍遷密度矩陣和電荷轉移矩陣考察電子激發特征》(http://www.shanxitv.org/436)
1 原理
已知兩個電子態G、E的波函數,就可以構建它們之間的躍遷密度矩陣(下面特指單粒子躍遷密度矩陣):T(r|r')=T(r1|r1')=N*∫∫...∫|ΨG(x1,x2...xN)><ΨE(x1',x2...xN)| ds1 dx2 dx3... dxN 其中N是總電子數,x是自旋+空間坐標,s是自旋坐標,r是空間坐標。
躍遷密度矩陣含有兩個三維空間變量,即是六維變量,是沒法直接繪制的。或者說,如何圖形化來描繪它的辦法不是唯一的。本文討論的是一種比較常見、有效、簡單的圖形化分析躍遷密度矩陣的方法。
躍遷密度矩陣用原子中心基函數展開后就變成了含有兩個標號的矩陣p,這個矩陣可以根據基函數所屬的原子中心進一步收縮成以原子為標號的矩陣P,即使用這種方式變換:
P(A,B)=∑[i∈A]∑[j∈B] p(i,j)^2 i和j代表原子中心基函數,A和B代表原子
實際上變換方式也不是唯一的,比如可以將p(i,j)^2改為p(i,j)的絕對值,對最終圖像效果有一些影響,但定性結論是一致的。
以原子表示的躍遷密度矩陣的對角元,例如P(A,A),代表電子態躍遷造成的A原子的電荷變化的程度。而非對角元,比如P(A,B),代表電子躍遷時A原子與B原子間的電子-空穴的相干程度(某個態的密度矩陣的非對角元經常被當做鍵級,而兩個態之間的躍遷密度矩陣的非對角元就可以理解為躍遷時的“動態鍵級”,或者說相應兩個原子在這個過程中的關聯程度)。以原子編號作為橫、縱坐標,以顏色來表示數值大小來繪制躍遷密度矩陣,可以很方便地分析電子躍遷所涉及到的原子以及原子間相干范圍,對于較大的共軛分子來說尤為有用。
Multiwfn支持以這種方式繪制躍遷密度矩陣,此程序可以免費從http://www.shanxitv.org/multiwfn下載。
2 例子
這里以繪制下面這個分子的躍遷密度矩陣為例進行說明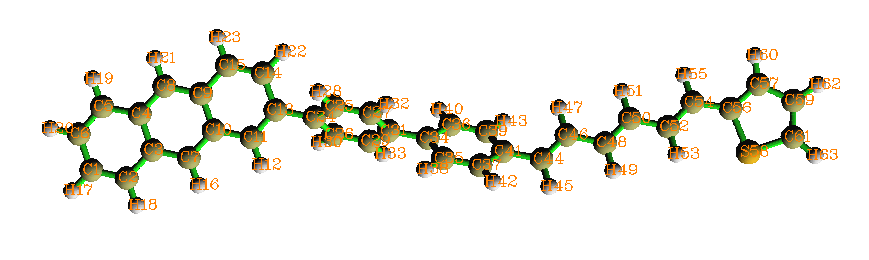
這個分子包含四個部分:蒽、兩個苯、己三烯、噻吩。由于分子略大,為了省時間,所以此例用半經驗方法ZINDO(亦稱INDO/S)來計算。
首先用Gaussian計算這個分子的激發態,輸入文件如下,結構已在PM6級別下優化,輸出文件假設叫tdmat.out。其中density=transition=1關鍵詞代表將S0->S1的躍遷密度矩陣傳遞給波函數分析模塊L601,而iop(6/8=3)表示L601模塊將會把傳遞來的躍遷密度矩陣輸出到輸出文件里。算完之后用formchk將tdmat.chk轉換為tdmat.fch。
%chk=C:\gtest\tdmat\tdmat.chk
#P zindo(nstates=10) density=transition=1 iop(6/8=3)
PM6 optimized
0 1
C -12.23469000 -1.59949700 -0.44519000
C -10.90485300 -1.89416000 -0.41362000
C -9.91985900 -0.84695000 -0.26327300
C -10.36853300 0.50925300 -0.14757300
C -11.78816300 0.77763200 -0.18600400
C -12.68490400 -0.23810600 -0.32928500
C -8.54611200 -1.12747500 -0.22848900
C -9.42758700 1.53918300 -0.00043800
C -8.05447200 1.25843200 0.03458600
C -7.60516500 -0.09749600 -0.08196600
C -6.18786600 -0.36800000 -0.04497800
H -5.86066100 -1.40374200 -0.13102800
C -5.28440700 0.64776600 0.10266900
C -5.73932300 2.01359000 0.22081600
C -7.06844500 2.30452500 0.18588200
H -8.20526000 -2.15857900 -0.31589600
H -12.98493200 -2.38050500 -0.55800000
H -10.55050800 -2.92028000 -0.50015200
H -12.11524200 1.81256100 -0.09714600
H -13.75638400 -0.04727400 -0.35946000
H -9.76850900 2.57024400 0.08779900
H -4.98900200 2.79603800 0.33001500
H -7.42269600 3.33146800 0.27016300
C -3.82937400 0.38281300 0.14497700
C -3.07180600 0.78122600 1.25797700
C -3.19872100 -0.26881300 -0.92659800
C -1.70051500 0.52722100 1.30039900
H -3.55871700 1.28369000 2.09318800
C -1.82581400 -0.51640200 -0.88722600
H -3.78299200 -0.57632400 -1.79332700
C -1.06859000 -0.12149600 0.22711800
H -1.11579500 0.83834500 2.16540700
H -1.34032200 -1.02376100 -1.72018900
C 0.38560400 -0.38681600 0.27068500
C 0.93813400 -1.12394500 1.33114400
C 1.22321500 0.09399200 -0.74751000
C 2.30850800 -1.37819000 1.37050900
H 0.29077900 -1.50435900 2.12071100
C 2.59623800 -0.15246000 -0.70346300
H 0.80002700 0.66719000 -1.57182400
C 3.15184900 -0.88857800 0.35651600
H 2.72818100 -1.95283500 2.19495600
H 3.23819700 0.22061400 -1.50028400
C 4.59389600 -1.16777300 0.41952300
H 4.85337000 -2.16976100 0.77201400
C 5.54066100 -0.27393200 0.08828100
H 5.27492800 0.73266200 -0.24674500
C 6.96872800 -0.57538800 0.16207400
H 7.23312600 -1.58986100 0.47261300
C 7.91759000 0.33277900 -0.13184300
H 7.65285400 1.34734100 -0.44101200
C 9.34483400 0.02984200 -0.05794900
H 9.60343700 -0.99039000 0.24037400
C 10.28940200 0.94828300 -0.33477700
H 10.01152800 1.97026400 -0.62174400
C 11.71085200 0.70883500 -0.28149600
C 12.73647700 1.61457500 -0.27342100
S 12.36627800 -0.91644100 -0.23061800
C 14.04355100 1.00496200 -0.21988900
H 12.61225000 2.68805400 -0.29889200
C 14.01162500 -0.35537800 -0.19207600
H 14.94474600 1.60386500 -0.20467900
H 14.83536500 -1.04594500 -0.15352900
啟動Multiwfn,然后依次輸入
tdmat.fch //Multiwfn做躍遷密度矩陣圖時需要讀入fch文件是為了從fch中得到各原子的元素和基函數與原子的編號對應關系
18 //電子激發分析
2 //繪制躍遷密度矩陣
tdmat.out //包含了躍遷密度矩陣的Gaussian輸出文件
1 //直接在屏幕上作圖
此時將立刻看到如下的圖像。注意,由于氫原子對于大共軛分子的電子躍遷幾乎沒有貢獻,所以作圖時默認不包含氫原子。因此橫縱坐標的編號和分子中的原子編號并不一致,氫原子被空過去了(如果想要讓氫原子也顯示,則選擇4 Switch if take into account hydrogens再作圖)。為了對應關系清楚,下圖坐標軸上的編號和相應重原子在分子中的位置在圖中直接標注了出來。
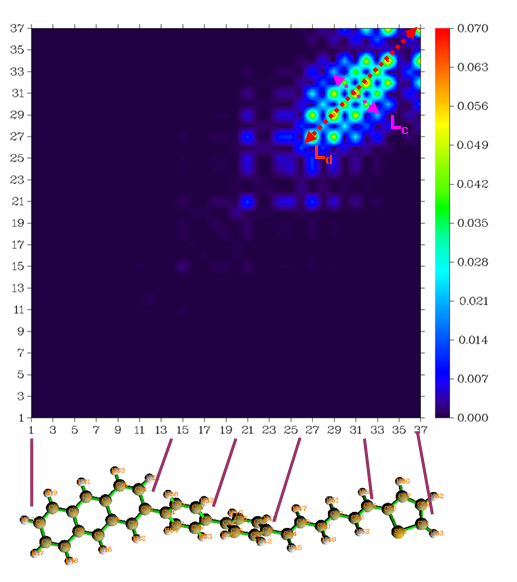
從圖中可見,數值比較大的部分都集中在圖的右上區域,這說明與這種激發模式主要涉及的是己三烯和噻吩部分的原子。紅色雙向箭頭表示的對角線區域是數值范圍整體較大的區域,其長度Ld表現了這種電子激發涉及的空間廣度。此圖中在靠近對角線的非對角元上也有很大數值,這說明在這種激發模式中主要涉及的原子與臨近原子有較強的電子-空穴相干性。圖中Lc值描述的對角線的帶狀區域越寬,代表原子間相干范圍越大。
利用NTO分析方法(見《使用Multiwfn做自然躍遷軌道(NTO)分析》http://www.shanxitv.org/377),也可以直觀地看出S0->S1激發確實是主要發生在己三烯和噻吩部分,這種激發模式的88%的特征可以由NTO 88->NTO 89的躍遷表現,以下是這兩個軌道的等值面圖
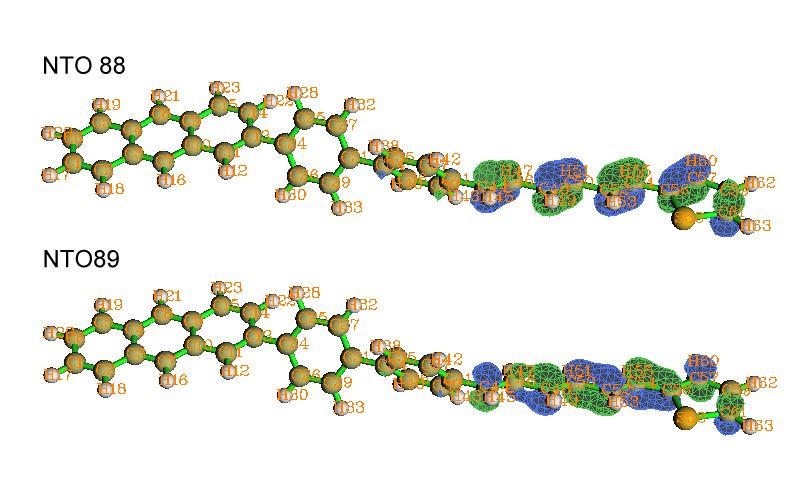
將density=transition=后面的數值改為感興趣的態的數值,重新計算得到含有相應躍遷密度矩陣的out文件,重復上面的步驟就可以作出基態到相應態的躍遷密度矩陣的圖。fch不必每次重新生成,對所有激發態來說其中要被用到的信息都是一樣的。
基態到S2、S3...一直到S10的躍遷密度矩陣圖如下所示
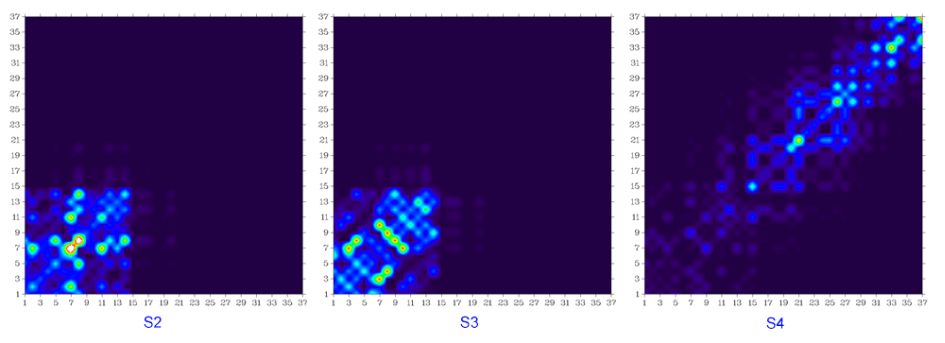
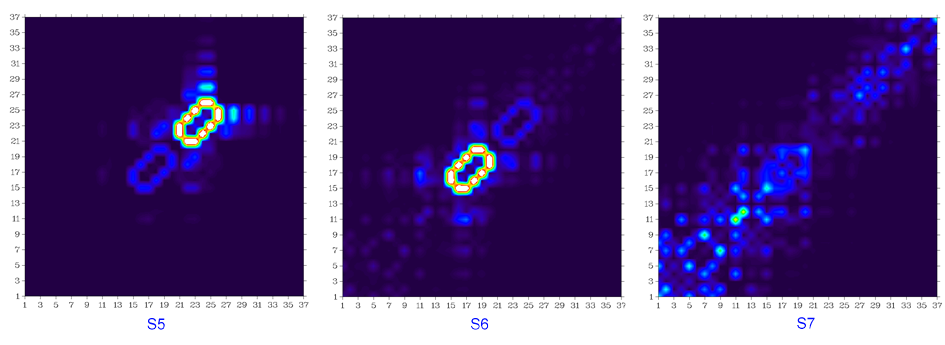
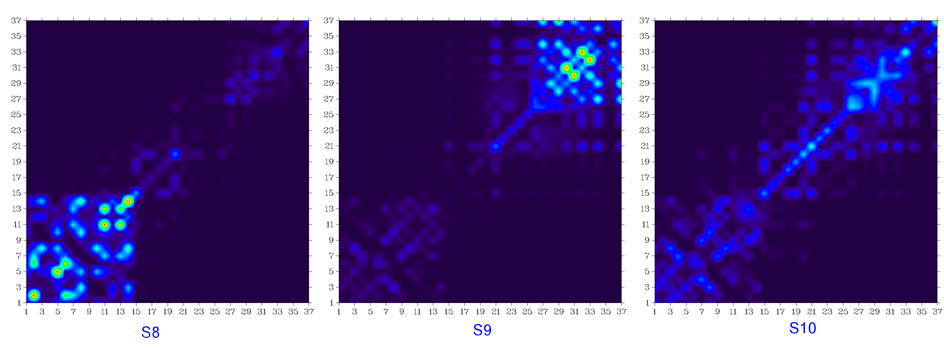
顯然,S0到S2、到S3、到S8的躍遷幾乎對應的都是蒽片段內的局部躍遷,由于蒽的很強的電子離域性,不難理解在這些躍遷中蒽片段內原子間有明顯相干性。S0到S5和到S6的躍遷很明顯分別幾乎只體現兩個苯環內的局部躍遷,并且環內相鄰原子在躍遷中相干性很強,這主要是由于結構的扭曲使苯環與周圍部分之間失去了很大程度的電子離域能力。諸如S0到S10的躍遷,由于在整個圖中的對角線及附近都有一定的數值,可知這種躍遷涉及到整個分子空間。
3 CIS、TDHF、TDDFT的情況
用CIS、TDHF、TDDFT方法,也可以按照上例方法來作圖,輸入文件和操作過程和上例沒什么區別,區別僅在于激發態輸入文件的route section。由于一些初學者對激發態計算不熟悉,這里廢話幾句。假設研究的是S2(1)用CIS的情況,route section寫為比如:#P CIS(nstates=5)/6-31G* density=transition=2 iop(6/8=3)
(2)用TDHF的情況,route section寫為比如:#P HF/6-31G* TD(nstates=5) density=transition=2 iop(6/8=3)
(3)用TDDFT的情況,route section寫為比如:#P B3LYP/6-31G* TD(nstates=5) density=transition=2 iop(6/8=3)
對于CIS、TDHF、TDDFT方式計算激發態,每次計算比ZINDO明顯耗時得多得多。假設用的是CIS方法,剛才分析完了S0->S1態,接下來想對比如S0->S4做分析,當然可以寫CIS/6-31G* density=transition=4 iop(6/8=3),但是這相當于完全地重算一遍,比較費時。較好的辦法是寫CIS(read)/6-31G* guess=read density=transition=4 iop(6/8=3),這說明在SCF過程中直接讀取check文件里已經收斂的SCF波函數,在CIS過程中(需要Davidson迭代求解)也直接讀取check文件里的初猜,這樣做會比起重算一遍速度會快不少。對于TDHF、TDDFT也是類似的,例如TDDFT時寫成B3LYP/6-31G* TD(read,nstates=5) guess=read density=transition=4 iop(6/8=3)即可。
補充說明1:在個別體系中,如果基組包含彌散函數,則Gaussian輸出的躍遷密度矩陣可能是錯的(起碼在G09 C.01中仍存在此問題),圖上表現的躍遷主要涉及的區域和考察躍遷主要涉及的MO的分布所得結論嚴重不符,這種情況不要用本文的分析方法,或者應當去掉彌散函數。
補充說明2:有時候會碰到一種情況,比如一個直鏈分子A---B,在Gaussian輸入文件里原子編號不是從左到右依次排下來的,而是混亂的,比如4號原子在左側,5號原子在右側,6號原子在中間...這種情況下顯然沒法把分子結構和躍遷密度矩陣圖中的坐標軸對應起來。解決方法就是重新對原子編號進行排序。比如先手動旋轉分子,讓A---B分子與X軸盡量平行,然后把輸入文件里的坐標都導入到excel里,對X坐標進行排序,然后再把排序過的原子坐標寫進高斯輸入文件里,這樣原子編號和原子在分子中的位置就對應起來了。重新計算并作圖后,分子結構就能像本文的例子一樣與躍遷密度矩陣圖的坐標軸進行對照了。